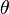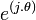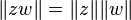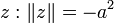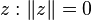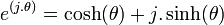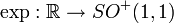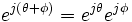Nombre complexe fendu - Définition
La liste des auteurs de cet article est disponible ici.
Propriétés algébriques
En termes d'algèbre générale, les nombres complexes fendus peuvent être décrits comme le quotient de l'anneau polynomial
![\mathbb{R}[x]\,](https://static.techno-science.net/illustration/Definitions/autres/3/3914300cd410f91c150f43ab2fb1cb4b_cf281c484e435894244a82ea4c5da34f.png)
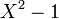
-
![\mathbb{R}[x]/(x^2 - 1)\,](https://static.techno-science.net/illustration/Definitions/autres/8/86ebf4b911dd37ab75f6b146410e3ddc_8ea652f98bc7dd02c296909f03e26bd3.png)
L'image de x dans l'ensemble-quotient est l'unité imaginaire j. Avec cette description, il est clair que les nombres complexes fendus forment un anneau commutatif de caractéristique 0. De plus, si nous définissons une multiplication scalaire de manière évidente, les nombres complexes fendus forment une algèbre associative et commutative sur les nombres réels de dimension deux. L'algèbre n'est pas un corps puisque les éléments nuls ne sont pas inversibles. En fait, tous les éléments nuls différents de zéro sont des diviseurs de zéro. Puisque l'addition et la multiplication sont des opérations continues en respectant la topologie usuelle du plan, les nombres complexes fendus forment un anneau topologique.
Les nombres complexes fendus ne forment pas une algèbre normée dans le sens usuel du mot puisque la « norme » n'est pas définie positivement. Néanmoins, si on étend la définition pour inclure les normes de signature générale, ils forment une telle algèbre. Ceci s'ensuit du fait suivant
Pour un exposé sur les algèbres normées de signatures générales, voir la référence par Harvey.
Les nombres complexes fendus sont un cas particulier d'une algèbre de Clifford. Nommément, ils forment une algèbre de Clifford sur un espace vectoriel à une dimension avec une forme quadratique définie négativement. Comparer ceci avec les nombres complexes qui forment une algèbre de Clifford sur un espace vectoriel à une dimension avec une forme quadratique définie positivement. (NB : certains auteurs permutent les signes dans la définition d'une algèbre de Clifford ce qui interchangera le sens de définie positivement et de définie négativement).
Géométrie
L'ensemble des points z tels que
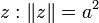

avec une branche supérieure et inférieure passant par ja et - ja. L'hyperbole et l'hyperbole conjuguée sont séparée par deux asymptotes diagonales qui forment l'ensemble des éléments nuls :
Ces deux droites (parfois appelées le cône nul) sont perpendiculaires et ont des pentes de
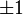
L'analogue de la formule d'Euler pour les nombres complexes fendus est
Ceci peut être déduit du développement en série de puissances utilisant le fait que cosh a seulement des puissances paires tandis que sinh a des puissances impaires. Pour toutes les valeurs réelles de l'angle hyperbolique
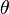
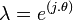
Puisque



L'ensemble de toutes les transformations du plan complexe fendu qui préserve la norme (ou de manière équivalente, le produit interne) forme un groupe appelé le groupe orthogonal généralisé O(1,1). Ce groupe est constitué des rotations hyperboliques - qui forme un sous-groupe noté
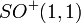
-
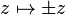
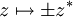
qui associe