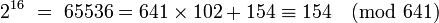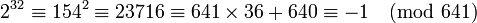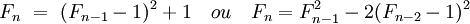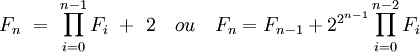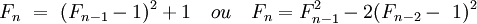Nombre de Fermat - Définition

Propriétés

Premières propriétés

La suite des nombres de Fermat possède plusieurs relations de récurrence. On peut citer par exemple si n est supérieur ou égal à 2 :

Ou encore, avec des produits de nombres de Fermat :

On en déduit le théorème de Goldbach affirmant que :

• Deux nombres de Fermat distincts sont premiers entre eux.

Soit D(n, b) le nombre de chiffres utilisés pour écrire F_n en base b.

• La valeur de D(n,b) est donnée par la formule suivante :

Les crochets désignent la fonction partie entière et log_b le logarithme de base b.

• Aucun nombre de Fermat n'est somme de deux nombres premiers à l'exception de F₁ = 2 + 3.
• Aucun nombre de Fermat n'est la différence de deux puissances de nombres premiers impairs.
• La somme des inverses de tous les nombres de Fermat est irrationnelle.

• 

En effet :

• 

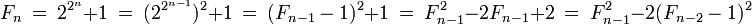
Une récurrence et l'égalité suivante permet de calculer le premier produit :

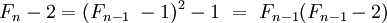
La seconde égalité s'en déduit :

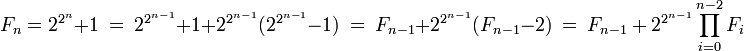
• Deux nombres de Fermat distincts sont premiers entre eux.

Soit n et m deux entiers positifs tel que n est strictement plus grand que m. Montrons que le seul facteur commun à F_n et F_m est 1. Un calcul précédent montre que :

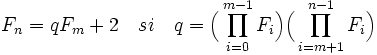
Donc un diviseur commun à F_n et F_m est aussi un diviseur de 2. Or 2 ne divise pas F_n, ces trois entiers sont donc premiers entre eux deux à deux.

• La valeur de D(n,b) est donnée par la formule suivante :

Il suffit de remarquer que le nombre de chiffres nécessaire pour écrire un entier a en base b est égal à la partie entière de log_b(a).

 

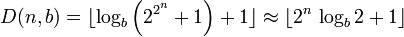
Nombre de Fermat et primalité

La raison historique de l'étude des nombres de Fermat est la recherche de nombres premiers. Fermat connaissait déjà la proposition suivante :

• Soit k un entier, le nombre 2^k + 1 est un nombre premier seulement si k est une puissance de deux.

Pierre de Fermat a conjecturé que la réciproque était vraie, il a montré que :

F₀ = 3 est premier

F₁ = 5 est premier

F₂ = 17 est premier

F₃ = 257 est premier

et F₄ = 65537 est premier

Actuellement, on ne connaît que cinq nombres de Fermat premiers, ceux cités ci-dessus.

On ignore encore s'il en existe d'autres, mais on sait que les nombres de Fermat F_n, pour n entre 5 et 32, sont tous composés ; F₃₃ est le plus petit nombre de Fermat dont on ne sait pas s'il est premier ou composé.

Le plus grand nombre de Fermat dont on sait qu'il est composé est actuellement F_{2 478 782}.

• Soit k un entier, le nombre 2^k + 1 est un nombre premier seulement si k est une puissance de deux.

Si k n'est pas une puissance de deux, alors il existe deux entiers a et b tel que a est impair et différent de un et a.b = k. On dispose alors des égalités suivantes :

Ce qui montre que 2^b + 1 divise 2^k + 1 qui ne peut donc être premier.

 

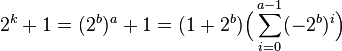
Factorisation des nombres de Fermat composés

Euler utilise une méthode de Fermat pour démontrer que F₅ n'est pas premier. Il démontre pour cela trois propositions :

• Un facteur premier du nombre de Fermat F_n est de la forme k. 2 ^m + 1 où k est un entier impair, et m > = n + 2.

• L'entier k de la proposition précédente possède un facteur premier impair.

• F₅ est divisible par 641.

Le cas général est un problème difficile du fait de la taille des entiers F_n, même pour des valeurs relativement faibles de n. À la date du ..., le plus grand nombre de Fermat dont on connaisse la factorisation complète est F₁₁^{[réf. souhaitée]}, dont le plus grand des cinq diviseurs premiers a 560 chiffres (la factorisation complète de F_n, pour n entre 5 et 10, est, elle aussi, entièrement connue). En ce qui concerne F₁₂, on sait qu'il est composé mais c'est, à la date du 27 mars 2010, le plus petit nombre de Fermat dont on ne connaisse pas la factorisation complète. Quant à F₂₀, c'est, à la date du 3 février 2010, le plus petit nombre de Fermat composé dont on ne connaisse aucun diviseur premier

• Un facteur premier p du nombre de Fermat F_n est de la forme k 2ⁿ⁺¹ + 1 où k est un entier.

F_n est congru à zéro modulo p. On en déduit que 2²ⁿ est congru à -1 modulo p et 2²ⁿ⁺¹ à 1 modulo p.

Montrons que l'ordre multiplicatif de 2 est 2ⁿ⁺¹ dans l'anneau Z/pZ. Soit m l'ordre multiplicatif de 2, m est un diviseur de 2ⁿ⁺¹, donc il existe un entier θ tel que m = 2^θ. L'entier 2^2θ est congru à un modulo p donc si h est un entier strictement supérieur à θ, 2^2h est aussi congru à un modulo p, si θ est strictement plus petit que n + 1 alors 2²ⁿ est congru à un modulo p ce qui est faux car nous avons montré qu'il est congru à -1.

De plus, le petit théorème de Fermat montre que 2^p-1 est congru à un modulo p. Ce résultat et le fait que l'ordre multiplicatif de 2 est 2ⁿ⁺¹ dans Z/pZ montre que p - 1 est un multiple de 2ⁿ⁺¹. Ce qui termine la démonstration.

• L'entier k de la proposition précédente possède un facteur premier impair.

Si k est une puissance de deux, alors p est un nombre premier de Fermat différent de F_n, or les nombres de Fermat n'ont pas de facteur commun. Cette remarque termine la démonstration.

• F₅ est divisible par 641.

Un diviseur premier de F₅ est de la forme 64.k + 1. Les valeurs de k possibles sont 3, 5, 6, 7, 9, 10 ... Les valeurs 5 et 6 ne correspondent pas à des nombres premiers, les valeurs à tester sont donc 193, 449, 557 et 641. Euler limite donc l'étude à quatre cas au lieu de plus d'une centaine. Etudions le cas où k est égal à 10.

Ce qui montre que 2³² + 1 est congru à zéro modulo 641 et la proposition est démontrée.