Nombre figuré - Définition

Introduction

En arithmétique, un nombre figuré est un nombre entier qui peut être représenté par un ensemble de points disposés de façon plus ou moins régulière et formant une figure géométrique.

Les nombres figurés sont d'origine très ancienne. On attribue parfois à Pythagore les premières études de nombres figurés (nombres carrés). Diophante a résolu plusieurs problèmes les concernant. Pascal a écrit un traité sur le sujet.

Exemple de nombres figurés

Les nombre figurés les plus simples sont

• Les nombres carrés

1	4	9

• Les nombres triangulaires

1	3	6

• Les nombres hexagonaux centrés

1	7	19

Ils correspondent par exemple à la répartition des cônes de couleur au centre de la rétine.

• Les nombres cubiques:

1 8 27 64

qui dessinent un cube dans l'espace

• Les nombres figurant sur les faces d'un dé cubique:

1	2	3	4	5	6

Classification

On range les nombres figurés suivant la dimension de la figure représentée. Celle-ci est très fréquemment un polytope et le nombre est alors appelé un nombre polytopique.

En dimension un

• les nombres linéaires

ce sont les entiers classiques

En dimension deux

• Les nombres polygonaux (triangulaires, carrés, pentagonaux, hexagonaux, heptagonaux, octogonaux ou gnomoniques)
• les nombres polygonaux centrés (carrés, pentagonaux, hexagonaux, heptagonaux, octogonaux)

En dimension trois

• nombres tétraédriques
• nombres cubiques ou cubiques centrés

En dimension supérieure

Les nombres figurés ne sont plus représentables par des figures correspondant au monde tangible mais sont considérés comme des vues de l'esprit

• nombre hypersolide (en dimension quatre)
• nombre Dn (en dimension n)

Une transversale

Il existe une liste de nombre figuré évoluant à la fois sur la taille de la figure et sur la dimension qu'elle détermine : ce sont les nombres r - topiques

• nombres linéaires en dimension un
• nombres triangulaires en dimension deux
• nombres tétraédriques en dimension trois
• nombres pentatopiques en dimension 4

Le nombre - topique de rang n est donné par la formule

est la factorielle de r, est un coefficient binomial, et est la factorielle croissante.

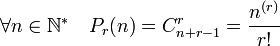
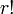
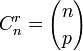
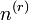
Les nombres polytopiques pour r = 2, 3, et 4 sont

• (nombres triangulaires)
• (nombres tétraédriques)
• (nombres pentatopiques)

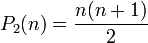
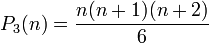
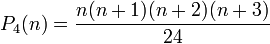
Pistes d'exploration

Le premier contact que tout être pensant entretient avec le nombre passe par le nombre figuré. C'est un langage universel non lié à l'écriture et aux systèmes de numération. Le nombre figuré permet de prouver que certains animaux (le poulpe par exemple) ont une conscience du nombre. En pédagogie, le passage par le nombre figuré permet de visualiser des propriétés comme la commutativité ou l'associativité des lois d'addition et de multiplication – lois qui leur sont dictées en construisant des rangées ou des tables de points. La relation 2 + 3 = 3 + 2 = 5, par exemple, qui traduit le fait que 2 et 3 sont permutables pour l'addition, peut être représentée par

+ = + =

Et la relation 2×3 = 3×2 = 6 (qui traduit le fait que 2 et 3 sont permutables pour la multiplication) peut être représentée par

2×3	3×2	6

On voit que on peut passer d'un rectangle à l'autre par rotation de 90° donc sans changer le nombre d'éléments. D'autre part, la somme est la simple juxtaposition des lignes des rectangles.

L'étude des nombres figurés consiste en général à trouver une relation entre le nombre lui-même et son rang dans la série. Par exemple, le nombre triangulaire de rang n est . Le nombre cubique de rang n est . Les concepts des nombres figurés font intervenir implicitement le concept moderne de récurrence.

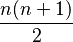
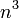
Une deuxième voie de recherche est de déterminer les propriétés des nombres figurant dans une même série. Par exemple, il est facile de montrer qu'il n'y a aucun nombre premier parmi les nombres triangulaires (sauf 3), carrés ou rectangles.

Une autre voie de recherche est d'utiliser les nombres figurés dans des résolutions d'équation dans comme l'extraction de racine carré et de racine cubique.