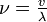Onde sur une corde vibrante - Définition

Modes propres de vibration d'une corde

Recherchons une solution de l'équation d'onde qui soit harmonique dans le temps, en posant

On trouve ainsi comme équation :

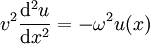
d'où

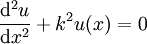
avec . La solution générale de l'équation ci-dessus est :

u(x) = Acoskx + Bsinkx

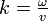
où A et B sont deux constantes d'intégration. Si la corde est de longueur L et fixée à ses 2 extrémités (x = 0 et x = L), on doit imposer comme conditions aux limites u(0) = u(L) = 0. La première condition impose que A = 0 et la seconde donne BsinkL = 0.

A part la solution triviale B = 0 (qui implique u = 0, ce qui n'a aucun intérêt), cette condition est aussi satisfaite si kL = π,2π,.... On trouve ainsi une famille de solutions :

.

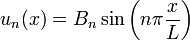
Pour lesquelles les pulsations sont .

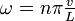
Les fréquences correspondantes sont , c’est-à-dire multiple d'une fréquence fondamentale (inverse du temps d'un aller et retour le long de la corde). Pour la présentation des effets de raideur, qui augmentent les fréquences propres d'autant plus que le numéro du mode propre est plus élevé, voir : Inharmonicité du piano.

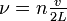
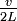
Il existe donc une infinité de modes propres de vibration, décrits par :

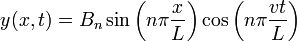
Les amplitudes B_n sont arbitraires.

La solution générale de l'équation d'onde peut s'écrire sous la forme d'un superposition de tous les modes propres :

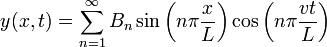
A l'instant t = 0, en particulier,

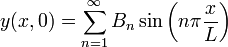
Si on se donne la forme initiale de la corde, c’est-à-dire si on suppose comme la fonction f(x) = y(x,0), les B_n représentent les coefficients d'une série de Fourier en sinus de f(x):

.

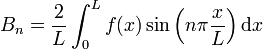
Équation d'onde pour une corde tendue

Tout ce qui suit suppose que la corde sonore est sans raideur et de diamètre nul, ce qui n'est jamais rigoureusement vérifié. Pour la présentation des effets de raideur, voir : Inharmonicité du piano.

La corde initialement au repos occupe un segment le long de l'axe des x. Elle est tendue avec une tension T (Force) appliquée à ses 2 extrémités. On déforme la corde dans la direction y et on la lâche. Appelons y(x,t) le déplacement de la corde à l'abscisse x et à l'instant t.

Ecrivons l'équation de Newton (Lois de Newton) pour une portion de corde à l'aplomb du segment [x,x + dx]. Aux extrémités on a les forces et de module T s'exerçant tangentiellement.

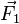
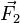
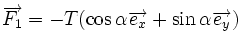
On suppose la déformation petite, de sorte que les angles sont petits :

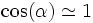
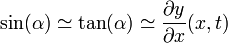
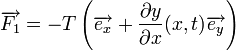
De la même manière, à l'autre extrémité située en x + dx

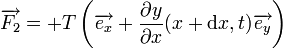
D'où :

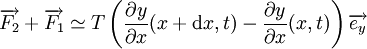
Par le théorème de Taylor limité au 1^er ordre (dx est supposé très petit) on obtient :

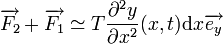
Par la seconde loi de Newton (F = ma), on aura en négligeant la force de la pesanteur :

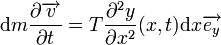
Où dm = μdx est la masse de l'élément de corde. En première approximation tous les éléments de la portion de corde ont la même vitesse transversale v_t dans la direction y, à ne pas confondre avec la vitesse longitudinale v définie ci-dessous et qui s'écrit :

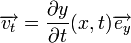
On en déduit :

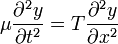
ou encore :

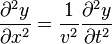
où

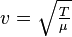
Il s'agit d'une équation aux dérivées partielles pour la fonction de deux variables y(x,t) appelée équation d'onde de d'Alembert à une dimension.

Signification de v comme vitesse de propagation d'une déformation.

Supposons que la corde est infinie. Dans ce cas, une solution possible de l'équation d'onde est : y(x,t) = f(x − vt) où f est une fonction arbitraire d'une variable qui est x − vt.

Remarque : y(x,t) = f(x + vt) est aussi une solution acceptable, mais correspond à une onde se propageant dans le sens des x négatifs.

L'équation est en effet satisfaite pour tout f. En particulier, si on pose t = 0, on a

f(x) = y(x,0) : déformation initiale de la corde en t = 0

A l'instant t₁, on retrouve la même forme mais déplacée en vt₁.

La déformation s'est propagée de vt₁ pendant le temps t₁, avec une vitesse v, sans subir de déformation.

Si, à l'instant t = 0, on a à faire à une déformation de type cosinusoïdale :

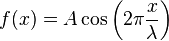
où λ est la longueur d'onde, on trouve à chaque instant :

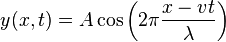
que l'on peut ré-écrire sous la forme:

où est le nombre d'onde et est la pulsation.

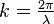
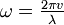
La fréquence est donnée : et ω = kv.