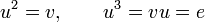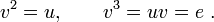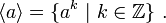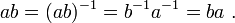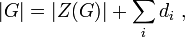Ordre (théorie des groupes) - Définition

Introduction

En théorie des groupes, une branche des mathématiques, le terme ordre est utilisé dans deux sens intimement liés :

• L'ordre d'un groupe est son nombre d'éléments si ce groupe est fini, et l'infini sinon.
• L'ordre (ou la période) d'un élément a d'un groupe est le plus petit nombre entier positif m tel que a^m = e (où e désigne l'élément neutre du groupe, et où a^m désigne le produit de m éléments égaux à a). Si aucun m de la sorte n'existe, a est dit d'ordre infini.

L'ordre d'un groupe G se note ord(G), |G| ou #G, et l'ordre d'un élément a se note ord(a) ou |a|.

Exemple

Le groupe symétrique S₃, constitué de toutes les permutations de trois objets, possède la table de multiplication suivante :

•	e	s	t	u	v	w
e	e	s	t	u	v	w
s	s	e	v	w	t	u
t	t	u	e	s	w	v
u	u	t	w	v	e	s
v	v	w	s	e	u	t
w	w	v	u	t	s	e

Ce groupe possède six éléments, si bien que

.

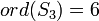
Par définition, l'ordre de l'élément neutre, e, est 1. Chaque carré de s, t, et w est égal à e, donc ces éléments du groupe sont d'ordre 2. En complétant l'énumération, u et v sont tous deux d'ordre 3, car

et

Lien entre les deux concepts

L'ordre d'un élément a est égal à l'ordre du sous-groupe engendré par a, qui est

L'ordre d'un élément de G divise l'ordre du groupe G (par exemple le groupe symétrique S₃ ci-dessus est d'ordre 6, et les ordres de ses éléments sont 1, 2 ou 3). Plus généralement, le théorème de Lagrange assure que l'ordre d'un sous-groupe quelconque H de G divise l'ordre de G (l'entier ord(G)/ord(H), noté [ G : H ], est appelé l'indice de H dans G).

La réciproque partielle suivante est vraie si G est un groupe fini : le théorème de Cauchy assure que si p est un nombre premier qui divise l'ordre de G, alors il existe dans G un élément d'ordre p (la condition que p soit premier est indispensable : par exemple le groupe de Klein n'a pas d'élément d'ordre quatre). On peut utiliser ce théorème pour montrer qu'un groupe fini est un p-groupe si et seulement si chacun de ses éléments a pour ordre une puissance de p.

Structure de groupe

L'ordre d'un groupe et l'ordre de ses éléments donnent des informations sur la structure du groupe. Informellement, plus la décomposition de l'ordre est compliquée, plus le groupe l'est.

Le seul groupe d'ordre 1 (à isomorphisme près) est le groupe trivial.

Le seul élément d'ordre 1 d'un groupe est l'élément neutre.

Un élément est d'ordre 2 si et seulement s'il est égal à son inverse, et différent de l'élément neutre.

Un groupe dont tout élément est d'ordre 2 (sauf l'élément neutre) est abélien puisque dans un tel groupe,

Mais la réciproque est fausse : il existe des groupes abéliens possédant des éléments d'ordre autre que 1 ou 2, par exemple le groupe additif Z / 6 Z des entiers modulo 6 est abélien (et même cyclique), mais la classe de 2 modulo 6 est d'ordre 3 (car 2+2+2=6 est congru à 0 modulo 6).

Autres propriétés

• Si G est un groupe fini d'ordre n et d est un diviseur de n, alors le nombre d'éléments dans G d'ordre d est un multiple de φ ( d ), où φ est la fonction indicatrice d'Euler, donnant le nombre d'entiers positifs inférieurs à d et premiers avec lui. Par exemple, dans le cas de S₃, φ ( 3 ) = 2, et nous avons exactement deux éléments d'ordre 3. Le théorème ne fournit pas d'information utile à propos des éléments d'ordre 2, parce que φ ( 2 ) = 1.

• Les morphismes de groupe ont tendance à réduire les ordres des éléments :

Si f : G → H est un morphisme, et a est un élément de G d'ordre fini, alors ord(f(a)) divise ord(a). Par exemple, le seul morphisme h : S₃ → Z/5Z est le morphisme nul, parce que chaque nombre sauf zéro dans Z/5Z est d'ordre 5, qui ne divise pas les ordres 1, 2 et 3 des éléments de S₃.

Si f est injectif, alors ord(f(a)) = ord(a). Ceci permet de montrer que deux éléments conjugués ont le même ordre, et par ailleurs, peut souvent être utilisé pour démontrer qu'il n'existe pas d'homomorphisme injectif entre deux groupes donnés.

• Un résultat important à propos des ordres est l'équation des classes ; elle relie l'ordre d'un groupe fini G à l'ordre de son centre Z(G) et aux tailles de ses classes de conjugaison non triviales :

où les d_i sont les tailles des classes de conjugaison non triviales ; ces tailles sont des diviseurs propres de |G| plus grands que un, car elles sont égales aux indices de certains sous-groupes propres non triviaux de G. Par exemple, le centre de S₃ est juste le groupe trivial, et l'équation se lit : | S₃ | = 1 + 2 + 3.

• De profonds problèmes et théorèmes de William Burnside mettent en jeu les notions d'ordre d'un groupe et de ses éléments ; certaines de ces questions sont encore ouvertes.