Paradoxe des jumeaux dans les espaces compacts - Définition

Introduction

Le paradoxe des jumeaux dans les espaces compacts est une extension du paradoxe des jumeaux de Langevin dans le cadre d'un espace-temps dont la partie spatiale possède une topologie « fermée ». Plus correctement exprimé, la partie spatiale de ces espace-temps est un espace compact.

Explications

Ici, Bernard se contente de faire le « tour de l'univers » à vitesse constante en suivant une trajectoire « fermée » de l'espace alors qu'Alain y reste immobile. Comme Bernard ne fait jamais demi-tour, il ne subit aucune accélération. La situation semble totalement symétrique entre Alain et Bernard mais c'est faux car dans un espace-temps de partie spatiale compacte (même s'il est plat et statique comme c'est le cas de l'espace-temps statique hypertorique par exemple) la relativité restreinte ne s'applique pas. En effet, la symétrie relativiste y est violée globalement. Dans ces espaces-temps, malgré l'absence d'accélération du jumeau en mouvement, cette violation (à l'origine d'une famille de référentiels inertiels privilégiés que l'on peut qualifier d'immobiles) suffit à lever le « paradoxe » de la dissymétrie de vieillissement du jumeau en mouvement de translation uniforme par rapport au vieillissement de son jumeau immobile.

En fait, la dissymétrie des effets relativistes se manifestant dans les espaces-temps de partie spatiale compacte, présente une forte analogie avec la dissymétrie de ces mêmes effets dans les référentiels en rotation (effet Sagnac), dilatation temporelle non réciproque de Lorentz applicable aux horloges tournantes et contraction circonférentielle non réciproque de Lorentz applicable aux mètres tournant). La compréhension de la dissymétrie de vieillissement des jumeaux, de la contraction de Lorentz du mètre du jumeau en mouvement et de l'analogue de l'effet Sagnac dans les espaces compacts (anisotropie de la vitesse relative de la lumière dans le référentiel inertiel de repos du jumeau en mouvement) est facilitée par cette correspondance. Ces effets non réciproques ont en effet déjà été analysés dans le cas des référentiels en rotation.

Il y a toutefois une difficulté. Dans l'espace-temps statique hypertorique, par exemple, dans un voisinage de n'importe quel événement, la métrique est de Minkowski. On pourrait être tenté de croire que la symétrie des effets relativistes reste donc applicable. Cela peut y rendre le paradoxe de Langevin déroutant si on n'a pas compris la différence entre symétrie locale et symétrie globale. En effet, la topologie de cet espace-temps est la cause de l'existence de référentiels inertiels privilégiés. On a du mal à l'admettre (et à admettre la dissymétrie des effets relativistes qui en découle naturellement) si on est un peu trop habitué à l'absence de référentiels inertiels privilégiés propre à l'espace-temps de Minkowski.

Cette difficulté de compréhension est facilement surmontée si l'on a compris comment mettre en évidence, dans ce cadre, une classe de référentiels inertiels privilégiés que l'on peut qualifier de référentiels inertiels immobiles. On y parvient en réalisant une synchronisation des horloges distantes par envoi de signaux lumineux partant de deux émetteurs situés à mi-distance de ces deux horloges sur chacune des deux portions de trajectoire faisant le tour de l'univers et passant par ces deux horloges (quand la trajectoire qui passe par ces deux horloges se referme sur elle-même, ces deux horloges se déplaçant à vitesse constante sur cette trajectoire). Les référentiels inertiels immobiles dans cet espace-temps se distinguent par le fait que la double synchronisation de ces horloges donne systématiquement lieu à une définition unique de leur simultanéité (pas de conflit entre les deux synchronisations, conflit de synchronisation analogue à l'effet Sagnac quand ces horloges sont en mouvement à une même vitesse v non nulle). Cette méthode de double synchronisation identifie les référentiels inertiels immobiles dans l'espace-temps statique hypertorique et permet du même coup d'y définir une simultanéité universelle (la simultanéité ayant cours dans les référentiels inertiels immobiles dans cet espace-temps).

Nous allons regarder d'un peu plus près une seule situation.

Alain est immobile dans un espace-temps statique hypertorique mais il n'en sait rien. Tant qu'il n'a accès qu'à des effets locaux, il croit que son espace-temps est un espace-temps de Minkowski. En effet, localement, il n'a pas connaissance des effets globaux (violant l'invariance relativiste) qui lui permettraient de réaliser son erreur. Conscient des seuls effets locaux, il croit donc naïvement que la notion d'immobilité n'a pas de sens physique dans son espace-temps (l'absence de notion objective d'immobilité exprime invariance dite de Lorentz c’est-à-dire la relativité du mouvement de translation à vitesse constante).

Bernard fait un tour d'univers. Il quitte Alain et revient près de lui après un certain temps (qui peut être très long si les dimensions caractéristiques de l'univers sont très grandes, ce n'est pas le genre d'expérience expérimentalement facile à réaliser, contrairement aux autres situations envisagées dans le cadre des référentiels tournants).

Les deux référentiels sont inertiels et il semble que l'on puisse appliquer la réciprocité de la dilatation du temps. Ainsi Alain, voyant Bernard en mouvement, constate (indirectement par échange d'informations avec des collègues situés dans le même référentiel inertiel) que les horloges de Bernard vont moins vite que les siennes. Quand Bernard revient auprès d'Alain, Alain constate que Bernard est effectivement plus jeune que lui. C'est donc bien Bernard qui voyage se dit-il à juste titre.

Bernard étant dans un référentiel inertiel, il croit pouvoir appliquer le même raisonnement. Il voit Alain s'éloigner à grande vitesse. Quand il le voit revenir auprès de lui (de l'autre côté), il doit pourtant se rendre à l'évidence. Alain a vieilli bien plus que lui. C'est donc Alain (et non lui) qui est resté immobile.

Nous retombons sur le paradoxe des jumeaux de Langevin et il se résout de façon similaire. La symétrie relativiste ne s'applique pas à cette situation. En effet, l'espace-temps statique hypertorique ne respecte pas globalement la symétrie relativiste.

Cette situation est plus difficile à justifier quand on l'a mal comprise. L'explication ci-dessous est elle-même basée sur l'étude des espaces compacts ainsi que sur une analyse détaillée de l'effet Sagnac. Ce n'est pas le genre de chose que l'on explique en cinq minutes (du moins si on tient à donner des tas de petits détails sans grand intérêt dans un premier temps). L'étude de l'effet Sagnac montre clairement les pièges des raisonnements compliqués, complication peu utile pour comprendre ce qui est essentiel car de nature à faire paraître compliquées des choses finalement assez simples. Cette façon compliquée de présenter des choses simples résulte souvent d'une mauvaise compréhension. Elle découle de l'attribution erronée d'un caractère de généralité au respect (valide seulement dans le cadre de l'espace-temps de Minkowski) d'une invariance globale des lois de la physique vis à vis des actions du groupe de Poincaré.

Le paradoxe de Langevin a parfois été utilisé par certains amateurs de relativité pour affirmer que dans les espaces compacts la Relativité Restreinte conduit à un paradoxe… C'est, bien sûr, tout à fait normal puisque la Relativité Restreinte (notamment la symétrie des effets relativistes) ne s'y applique pas.

Certains amateurs n'ayant pas compris les bases de la relativité, semblent avoir laissé échapper l'analogie entre la non réciprocité des effets relativistes dans les espace-temps de partie spatiale compacte et dans les référentiels tournants. Plus important encore, certains n'ont pas compris que la métrique de Minkowski est valide partout dans l'espace-temps statique hypertorique (un cas particulier d'espace-temps de partie spatiale compacte), mais que cela ne permet pas pour autant d'y appliquer la Relativité Restreinte (voir les références).

Revenons à l'explication du paradoxe de Langevin dans l'espace-temps statique hypertorique.

Dans le cas d'Alain, pas de problème. Son raisonnement est correct car il se trouve immobile dans un espace-temps de partie spatiale compacte dont la métrique est la métrique de Minkowski. C'est en fait identique à l'explication du paradoxe classique sauf que Bernard revient vers Alain sans faire demi-tour. Au lieu d'avoir le diagramme classique :

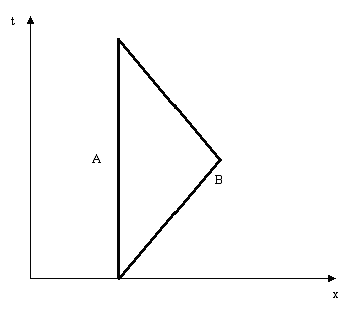
On a :

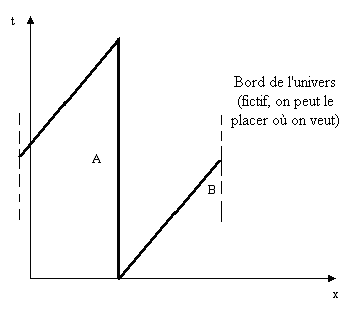
Les calculs sont les mêmes.

N'oublions pas que l'espace-temps considéré n'est pas un espace-temps de Minkowski. La dilatation du temps n'y est pas réciproque. En fait, c'est là que la difficulté se situe, la question se pose : tant qu'Alain s'éloigne un peu de Bernard on peut appliquer la réciprocité de la dilatation du temps. A partir de quand n'est-elle plus valable ?

La réponse est simple. La réciprocité apparente de la dilatation du temps est une illusion due à un manque d'information sur les effets globaux violant l'invariance de Lorentz (la relativité du mouvement). Le tour d'univers a un rôle essentiel : il permet à Alain et Bernard de comparer directement leurs vieillissements respectifs (sans recours à un choix arbitraire de référentiel inertiel de synchronisation). Cela fait apparaître la dissymétrie due au caractère privilégié du référentiel inertiel immobile d'Alain. Alain restant immobile, il est bien sûr plus vieux que Bernard lors de leurs retrouvailles.

Connaissant la vitesse v de Bernard et la longueur L de la trajectoire « fermée » parcourue par Bernard, vous pouvez vous amuser à « calculer » (le terme est un peu fort pour des « calculs » aussi simples) la durée propre T=L/v du voyage de Bernard, puis le vieillissement plus important d'Alain pendant le voyage de Bernard.

On peut aussi analyser cette situation sous l'angle de l'effet Doppler en n'oubliant pas que l'univers est « fermé ». Si Bernard se déplace sur une géodésique dont la projection spatiale (la trajectoire) est « fermée » de longueur L et s'il envoie des signaux lumineux dans les deux sens le long de sa trajectoire, il les reçoit tous les deux mais pas en même temps. Les signaux suivent des géodésiques lumières dans un espace-temps dont la topologie n'est pas celle de (topologie de l'espace-temps de Minkoski). Les trajectoires des rayons lumineux s'apparentent, bien sûr, à des hélicoïdes tracées sur une chambre à air. Le décalage δT des instants de réception des signaux lumineux émis en même temps par Bernard (quand il parcourt une trajectoire fermée de longueur L à la vitesse v dans l'espace-temps statique hypertorique) est semblable à celui de l'effet Sagnac. On a, bien évidemment :

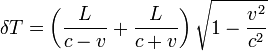
Enfin, le lecteur peut faire des petits calculs simples pour s'assurer qu'il a bien compris. Pourquoi pas calculer la contrainte de traction induite par la contraction de Lorentz pour un anneau élastique sans masse tournant dans cet espace-temps le long d'une trajectoire fermée de longueur minimale dans l'espace-temps statique hypertorique (c'est un calcul très simple qui prend moins d'une ligne) ?