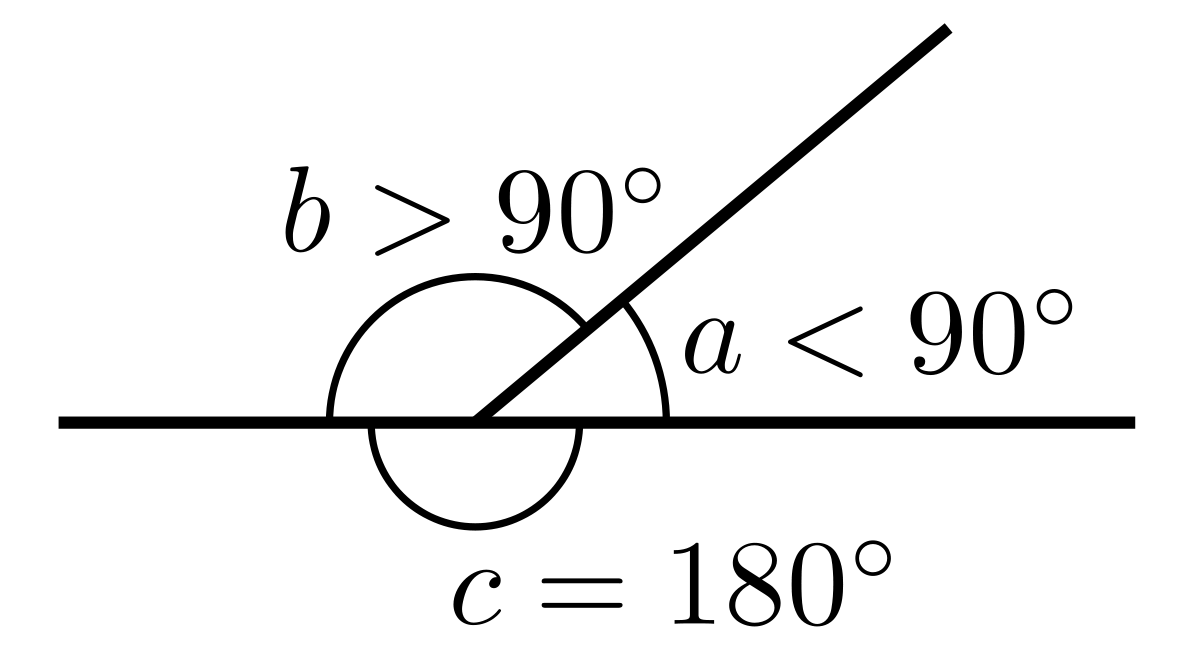Pierre Hérigone - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Pierre Hérigone, né vers 1570 (à Gigny-sur-Saône ?) et mort à Paris, vers 1643, est un mathématicien et astronome français. Son nom est latinisé sous la forme Petrus Herigonius.
Éléments biographiques
D'origine basque d'après Per Stromholm, on pense qu'il enseigna à Paris presque toute sa vie. Membre de l'Académie de Mersenne, il participa à plusieurs commissions scientifiques, dont l'une convoquée en 1634 par Richelieu. Celle-ci, comprenant Étienne Pascal, Jean de Beaugrand et Claude Mydorge, était chargée d'évaluer l'efficacité d'une méthode proposée par l'astronome Jean-Baptiste Morin pour trouver la longitude (en mer) d'après le mouvement apparent de la Lune. La commission ayant rendu un avis négatif sur les questions soulevées par Richelieu, Morin en voulut particulièrement à Hérigone qu'il pensait responsable de ce jugement.
Dans son Cursus mathématiques, Hérigone donne les raisons des erreurs de Morin : cinq causes qu'il attribue à la distance Terre-Lune, qui n'est pas constante, aux multiples observations qu'il faut faire simultanément, et aux réfractions dues à l'atmosphère. Un autre sujet de dissension entre les deux hommes est le refus qu'oppose Hérigone aux croyances astrologiques de Morin. Dans son cursus, il pousse sa critique jusqu'à écrire :
De lui, on sait d'après un propos de Charles Mallet, rapporté par Joseph-François Michaud et Louis Gabriel Michaud, qu'il fut un des plus fameux joueurs de dames de son temps.
« Surtout P. Hérigone. »
C'est la seule anecdote qu'on ait sur lui.
Sur la foi d'une indiscrétion de Claude Hardy, les historiens l'ont parfois identifié au linguiste Clément Cyriaque de Mangin, ou au mathématicien Denis Henrion.
Les apports d'Hérigone au calcul formel
L'un des derniers épigones de Viète
|

- Par son cours, Hérigone est le premier à populariser l'algèbre nouvelle de François Viète, à l'introduire à un niveau élémentaire d'apprentissage. Son identification avec Henrion pose d'autant plus de problème que Denis Henrion s'était opposé à Ghetaldi et Alexander Anderson, deux autres éditeurs de Viète, leur reprochant de n'avoir pas correctement résolu un problème posé en son temps par Regiomontanus. D'après Joël Biard et Rushdī Rāshid, qui établissent une filiation Viète-Hérigone-Descartes, son cours est reproduit dans "le calcul de monsieur Descartes" texte publié en mai juillet 1638 à la demande de Descartes par Godefroy de Haestrecht, un mathématicien hollandais résidant alors à Rhijnauwen, près d'Utrecht, et qui présente les fondements des mathématiques du philosophe de la Haye.
Hérigone définit l'algèbre dans les termes mêmes de Viète ; et pour lui :
« Elle (l'l'algèbre) se distingue en la vulgaire et en la spécieuse. L’Algèbre vulgaire ou nombreuse est celle qui se pratique par nombres. L’Algèbre spécieuse est celle qui exerce sa logique par les espèces ou formes des choses designées par lettres de l’alphabet. L’Algèbre vulgaire sert seulement à trouver les solutions des problèmes arithmétiques sans démonstration. Mais l’Algèbre spécieuse n’est pas limitée par aucun genre de problème, et n’est pas moins utile à inventer toutes sortes de théorèmes, qu’à trouver les solutions & démonstrations des problèmes. »
L'algèbre est indissolublement liée à la géométrie dans son esprit et il semble ignorer la publication des Regulae :
« Car d’un côté il est constant que la connaissance des nombres est absolument requise à la considération de la symétrie et à l'incommensurabilité de la quantité continue, desquelles la Géométrie fait un de ses principaux objets ; et d’autre part, il y a des démonstrations en notre arithmétique qui ne peuvent être entendues sans le secours des premiers livres des Eléments d’Euclide. »
Comme François Viète, Hérigone ignore les travaux des mathématiciens italiens Scipione del Ferro et Niccolo Tartaglia, et la publication qu'a fait Jérôme Cardan de leurs travaux et donne une formulation géométrique des résolutions d'équations de degré 2 et 3.
L'un des premiers précurseurs de Peano
- Hérigone est le premier à introduire la notation
- Il introduit également le symbole
- Pour les puissances d'un nombre, Hérigone écrit a, a2, a3, etc. (c'est-à-dire que les exposants n'était pas surélevés comme aujourd'hui, mais simplement postposés).
- D'autres symboles ont eu moins de fortune, ainsi 5< pour un pentagone ; ou ÷5< pour le côté d'un pentagone
- Certains symboles d'Hérigone sont ambiguës, témoin U pour vel ; l'égalité chez lui s'écrit 2|2, plus grand 3|2, plus petit 2|3 ; des confusions s'avèrent possibles.
- Parmi les connaissances qu'expose Hérigone, se trouve aussi bien de la géographie, un résumé de Stevin, de l'algèbre spécieuse de Viète, une version de la méthode des tangentes de Fermat, que l'exposé, vulgarisé du problème de détermination des Longitudes.
- L'ouvrage d'Hérigone contient également nombre de termes mathématiques utilisés depuis : Parallelipipedum (pour parallélépipède).