Jean de Beaugrand - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Jean de Beaugrand, né entre 1584 et 1588, mort à Paris le 22 décembre 1640, est un mathématicien français. Secrétaire royal, membre de l'académie de Mersenne, ami et correspondant de Hobbes, de Fermat et de Galilée, il défendit la mémoire de François Viète, dont il fut semble-t-il l'un des derniers élèves. Ennemi de Descartes, dont il dénonça les plagiats supposés, il soutint en 1636 que les graves ne pesaient rien au centre de la Terre. Pour cela, il reçut de Descartes le surnom méprisant de « géostaticien ». Secrétaire du roi et du trésor royal chargé de signer les privilèges d'édition, Jean de Beaugrand fut l'un des membres les plus influents de l'académie de Mersenne. Toutefois, en raison de ses polémiques et de ses démêlés avec Morin et Desargues, de sa désobligeante habitude (aux dires de Blaise Pascal et Paul Tannery) de s'approprier les travaux des autres membres de l'académie, dont ceux de Fermat et de Roberval, la postérité a conservé de lui une image plutôt négative. De nombreux historiens l'ont confondu avec son père, maître écrivain de Louis XIII, dont il édita les œuvres. Aucun travail de gravure, ni d'écriture ne peut, à priori, le rattacher aux maîtres écrivains. Il lui revient en revanche d'avoir donné son nom à la cycloïde.
Éléments biographiques
Fils du maître écrivain Jean de Beaugrand, secrétaire ordinaire de la chambre du roi (1590) et maître d'écriture du jeune Louis XIII en 1606, Jean II de Beaugrand a pour oncle Baptiste de Beaugrand, qui suit lui aussi une carrière de graveur et de maître écrivain. Viète étant mort en 1603, il est vraisemblable que le jeune Beaugrand soit resté peu de temps l'élève du fondateur de l'algèbre nouvelle. À ce titre, il serait l'un des rares élèves du mathématicien des Parthenay avec Nathanael Tarporley, Jacques Aleaume, Marin Ghetaldi et Alexander Anderson.
Découvreur de Fermat
En relation avec Mersenne, probablement dès le retour de celui-ci sur Paris, vers 1619, il prend contact avec le cercle des mathématiciens de Bordeaux, Étienne d'Espagnet, fils du président du Parlement de Bordeaux Jean d'Espagnet (un des amis de Viète), Philon et Prades, tous trois liés à Pierre de Fermat.
En 1626, il rencontre Fermat à Orléans, probablement en août. Certains auteurs ont contesté une telle rencontre. Une amitié certaine naît de leurs échanges et d'après Mahoney, Pierre de Fermat apprivoise les notations de Viète par l'entremise de Beaugrand (il en possède déjà un livre par d'Espagnet). C'est au travers de leur correspondance que Fermat se rend célèbre à Paris dans le cercle des scientifiques et des philosophes regroupés autour du Père Marin Mersenne ; la petite académie qui se réunit chaque semaine à l'Hôtel des Minimes, avec Pierre Gassendi, Étienne Pascal, le père de Blaise Pascal, Monsieur de Roberval; Pierre Petit, etc...
En 1630, Beaugrand devient le mathématicien attitré de Gaston d'Orléans, dont son oncle Baptiste de Beaugrand, était encore l'écrivain (vers 1628). Il publie une réfutation de la fausse duplication du cube de P. Yvon sieur de la Leu.
Éditeur de Viète
En 1630, Jean-Louis Vaulezard lui dédie sa traduction en français des Cinq Livres de Zététiques de Viète. Il lui écrit de façon fort louangeuse :
« Voulant fait voir la lumière à ce livre et le donner au public, j'ai cru deuoir imiter ceux, qui en de pareilles occasions font élection d'un homme dont le nom, posé au frontispice de leur œuvre, les autorise: Différent néanmoins du sentiment de la plupart d'iceux, qui n'ont égard qu'à la grandeur et à la qualité relevée de celui, auquel ils dédient leurs ouurages, sans se soucier s'il est capable de juger de la valeur du présent. Et c'est cette raison qui m'a fait vous choisir parmi tant de beaux esprits dont notre France est honorée, pour vous offrir les cinq Livres des Zététiques de feu Monsieur Viète, et ce d'autant plus volontiers, que je sais combien la mémoire de ce divin personnage vous est chère.. »
Et il ajoute, à ce premier compliment, l'espoir de voir Jean de Beaugrand restaurer l'algèbre de Viète
À cette époque, son protecteur Gaston d'Orléans doit s'enfuir en Lorraine puis aux Pays-Bas espagnols à la suite de ses démêlés avec Louis XIII. En 1631, Beaugrand fait publier un traité d'analyse spécieuse dans le droit fil de l'algèbre de Viète et quelques commentaires dont certains seront adoptés par Frans Van Schooten dans son édition en 1646, notamment le livre Ad logisticem speciosam Notas priores qui devait suivre l'Isagoge en 1591 et n'avait jamais été publié du vivant de Viète. Le 17 août 1632, il hérite de son oncle Baptiste de Beaugrand des planches de gravures, qu'il réunit avec celles qui lui venaient de son père, et en 1633, Beaugrand fait republier cher Henry le Gras leurs volumes sous une page de titre commune avec une dédicace à Louis XIII.
La commission Morin
Membre de l'académie de Mersenne, Beaugrand prend part aux rencontres chez le père minime. D'après Descartes, il se sont retrouvés chez Mersenne dès 1634 (et aussi en 1637).
En 1634, Beaugrand est nommé par le cardinal de Richelieu dans un jury chargé d'évaluer les travaux de l'astronome-astrologue Jean-Baptiste Morin. Ce dernier se proposait de donner une mesure du temps absolu à l'aide de l'observation de la Lune (y compris en mer). Le jury comprend Étienne Pascal, Claude Mydorge, Pierre Hérigone, Boulenger et de la Porte ; Beaugrand, d'un naturel mélancolique devait y tempérer ses collègues, plus passionnés. Leur querelle avec Morin s'étale sur cinq ans, et se conclut par une condamnation très sévère des thèses de l'astronome. Cette attaque contre Morin irrite Descartes, dont ce dernier est alors l'ami déclaré. Morin, croyant que le rapport que Beaugrand ferait de ses calculs ne pourrait que lui être favorable et lui concilier les autres commissaires, se montre grandement déçu à l'énoncé des réponses de la commission instituée par Richelieu :
- 1. La science des longitudes avait-elle été démontrée par quelqu'un avant la démonstration donnée par M. Morin ?
- 2. La démonstration de M. Morin est-elle bonne ?
- 3. La méthode est-elle praticable sur mer ?
- 4- Les Tables astronomiques peuvent-elles, par cette science, être en peu de temps rendues beaucoup plus exactes que par tous les moyens précédemment employés ?
Le 10 avril 1634, la réponse des six commissaires est entièrement négative. Jean-Baptiste Morin en rend responsable Pierre Hérigone et Jean de Beaugrand mais après la mort de Richelieu, Jean-Baptiste Morin, qui était un des tenants du géocentrisme et avait mis l'astrologie en vogue à la cour, fut amplement dédommagé de son échec par les largesses de Jules Mazarin, selon Paul Tannery.
Le 24 juin 1634 Jean De Beaugrand est reçu secrétaire du roi en remplacement d'un cousin de Gédéon Tallement
Un voyageur et un passeur
En 1635, Beaugrand est nommé secrétaire royal sous les ordres du chancelier Séguier qui est le bras droit de Richelieu pour tout ce qui concerne la police, la justice et plus généralement l'administration du royaume. Puis Beaugrand voyage quelques temps en Angleterre. Il rencontre Thomas Hobbes à plusieurs reprises. À partir de 1635 Beaugrand voyage en Italie, avec l'ambassadeur Bellièvre. Il y rencontre les mathématiciens Cavalieri, le 23 octobre à Bologne, Benedetto Castelli à Rome et Galilée, près de Florence, à qui il fait connaître les travaux de Pierre de Fermat. Il demeurera en correspondance avec eux après 1636.
Une lettre de Bonaventura Cavalieri témoigne de ce rôle de passeur que se donnait Beaugrand:
« Beaugrand m'a dit qu'un Sénateur de Toulouse (Fermat) avait proposé le problème suivant : décrire une parabole passant par quatre points donnés (sachant que ces points forment un quadrilatère dont deux côtés au moins ne sont pas parallèles), et qu'il l'avait résolu. »
Dans leur correspondance, Beaugrand et Fermat évoquent leurs sujets de recherche, la variation des graves (poids), l'arithmétique, le tracé des tangentes, que Beaugrand communique par la suite à Thomas Hobbes ou à Cavalieri. Ces échanges ont quelquefois valu au secrétaire royal la réputation de s'approprier un peu trop aisément les découvertes d'autrui. Vingt ans après la mort de Beaugrand, Blaise Pascal l'accuse en effet, dans son histoire de la roulette, d'avoir communiqué les inventions de Roberval et de Fermat sans mentionner explicitement leur auteur et en laissant penser à Bonaventura Cavalieri que ces inventions pouvaient venir de lui ; l'affirmation de Pascal ne semble pas fermement étayée, des lettres de l'abbé Castelliet de Cavalieri laissant entendre au contraire que Beaugrand leur avait fait connaître Fermat ou, tout au moins, que ce dernier ne leur était pas inconnu.
De même, en compulsant les échanges de Beaugrand et de Thomas Hobbes, Mahonay a pu penser que Beaugrand s'y donnait pour l'auteur des méthodes du toulousain Fermat mais cette indélicatesse a été récemment contestée.
La géostatique
- De la variation du poids des graves.
En février 1636, Beaugrand est de retour à Paris. Il publie chez Toussaint Du Bray le fruit de réflexions qu'il a eu avec Pierre de Fermat et les italiens Benedetto Castelli et Bonaventura Cavalieri en un livre de géostatique intitulé en latin : Geostatice seu de vario pondere gravium secundum varia a terrae (centro) intervalla tatio mathematica. C'est un essai de philosophie naturelle qui énonce une loi dérangeante (pour l'époque) quant à la variation du poids des corps : pour Beaugrand, appliquant des considérations de levier, les graves ne pèsent rien au centre de la Terre. Il a communiqué une partie de ces résultats à Galilée dans une lettre du 3 novembre 1635, et ses démonstrations sont attendues avec impatience. Mais son ouvrage déplaît aux autres membres de l'académie de Mersenne. Les idées en sont résumées ainsi par le Père minime :
« ...un corps pesant, par exemple une balle de plomb d'une livre, devient d'autant plus légère qu'elle s'approche du centre de la Terre, et elle ne pèse presque plus rien lorsqu'elle se joint audit centre, comme conclut M. de Beaugrand dans sa Géostatique, où il tient que la pesanteur de chaque corps se diminue en mesme raison qu'il s'approche davantage du centre de la Terre, et que mesme toute la Terre ne pèse point. »
Les équilibres que décrit Beaugrand pour justifier sa proposition principale (un grave pèse proportionnellement à sa distance au centre de la Terre) proviennent des conceptions d'Albert de Saxe. Elles ne sont pas nouvelles ; elles ont été reprises par Blasius de Parme, par Giovanni Battista Benedetti, Guidobaldo del Monte et Simon Stevin. Néanmoins Cette intuition contredit les notions dont les physiciens du XVIIe siècle ont hérité d'Aristote au travers de Jordan de Nemore. De plus, dans sa démonstration Beaugrand s'est appuyé sur une fausse interprétation du théorème des moments.
On trouve dans Tannery ces énoncés tirés pour les premiers d'Euclide ou de Ptolémée :
- « Si rectarum parallelarum extrema duabus rectissibi occurrentibus coniungantur, rectae ductæ sibi mutuo proportionaliter occurrunt. »
- « Si à punctis A, F rectarum A C, C F angulum in puncto C constituentium, deducantur rectae AD, FB qui sibi mutuo in puncto E et rectis AC, CF in punctis B, D occurrunt. Dico quod ratio rectæ AC ad rectam BC composita est ex ratione rectae AD ad rectam D E et ratione rectæ EF ad rectam BF »
- « Si rectae AC, CF angulum in puncto C constituunt, diuisâque » AC bifariàm in puncto B, ducatur BF, necnon et recta AD rectis BF, CF in punctis E, D occurrens. Dico quod recta AE ad rectam ED eandem habebit rationem quam recta CF ad rectam DF. »
- « Omne grave prope Terrae centrum minus pondérât quàm procul et eiusdem gravis varia pondéra eandem habebunt rationem quam à Terrae centro distantiae. » C'est la seule proposition à laquelle s'est attaché Descartes d'après Tannery et Baillet qui rapporte les mots du philosophe ;
« Je n' ay trouvé dans tout ce beau livre in folio qu' une seule proposition, quoique l' auteur en conte treize... et elle a déja été si bien réfutée par M De La Brosse qu' il n' est pas besoin d' y rien ajouter. »
- « Proposito gravi cuius in data à Terrae centro distantiâ notum sit pondus, invenire punctum in quo siapponatur sit dati cujus libet ponderis. »
- « Corpora gravia quorum pondérai sunt in eadem ratione quam à Terrae centro distantiai in aequali à Terrae centro distantiâ sunt eiusdem ponderis. »
- « Gravia in quâlibet aequali à Terrae centro distantia semper eandem retinent ponderis rationem. »
- « Si grauia ita à Terrae centro distiterint, ut ratio interuallorum sit reciproca rationi ponderum in aequali à Terrae centre distantia, gravia in dictis distantijs erunt ponderis ejusdem. »
- « Si duo gravia in quibusdam à Terrae centro distantis fuerint eiusdem ponderis, ratio distantiarum erit reciproca rationi ponderum in aequali à Terras centro diastemate. »
- « Datas rationes simul addere, atque datam rationem è data ratione subducere. Ratio ponderis corporum grauium in quibuslibet à Terrae centro distantis, est composita ex ratione distantiarum à Terrae centro et ratione ponderis in aequali à Terrae centro distantia. »
- « Gravia in Terrae centro nullam habent gravitatem. »
- « Sphaera terrestris nullam habet grauitatem. »
Pour Tannery, tous les raisonnements que Beaugrand fait ensuite (après la quatrième proposition) forment un tissu de paralogismes, que Descartes n'a pas trop sévèrement relevés et qualifiés (voir la polémique détaillée ci-dessous).
- Une vive polémique avec Desargues
Quand Girard Desargues critique vivement son traité, Beaugrand en retour critique le brouillon-projet de Girard Desargues sur les évènements de la rencontre d'un cône et d'un plan. Il conteste l'originalité des propositions, empruntées selon lui aux Coniques d'Apollonius. Il considère comme ridicule les noms que Desargues donne aux courbes d'Apollonius de Perge (défaillement pour ellipse, outrepassement pour hyperbole). Leur querelle s'envenime et leur amitié se mue en une opposition farouche. Beaugrand, défendant la géométrie classique contre les innovations du lyonnais Desargues, ne comprend pas le sens projectif de ces travaux novateurs. Desargues quant à lui ne trouve aucune grâce aux idées de géostatique du secrétaire royal Beaugrand.
D'après Adrien Baillet, Desargues (selon d'autres versions Mersenne lui-même) encourage le médecin-botaniste Guy de La Brosse à réfuter la statique de Beaugrand. Mais Beaugrand est puissant, et proche de l'État. Il intrigue contre Desargues, si bien et si fort qu'il s'attire les foudres de Descartes et que son amitié avec Fermat, d'un naturel charitable, s'en trouve quelque peu refroidie.
- Les critiques de Pierre de Fermat
Beaugrand n'a pas communiqué son livre au toulousain Fermat et celui-ci en est réduit à écrire à Mersenne, le 26 avril 1636 qu'il l’obligeriez beaucoup de lui faire savoir si Beaugrand est à Paris. C’est un homme dont il assure faire une estime très singulière ; Fermat lui trouve l’esprit merveilleusement inventif, et pense que sa Géostatique sera quelque chose de fort excellent.
Tenant lui aussi des principes d'Albert de Saxe, Pierre de Fermat propose alors quelques mois plus tard, ses propres calculs de la variation des graves. À l'époque, la distinction entre poids et masse n'est pas faite distinctement et le père minime Mersenne s'empresse de communiquer les démonstration de Fermat et de Beaugrand à ses amis géomètres. Une controverse s'en suit avec Roberval et Pascal. Ces derniers, plus avancés dans la compréhension des parallélogrammes de forces de Simon Stevin et les analyses de la gravitation en termes de force (suivant Johannes Kepler), découvrent à l'automne 1636 les erreurs de démonstrations de Fermat et de Beaugrand, essentiellement dues à de mauvaises applications du théorème des moments plus que leur croyance en la tendance du « centre de gravité d'un corps à s’unir au centre de la Terre ».
L'affrontement avec Descartes
En 1637, lors de la parution du Discours de la Méthode pour bien conduire sa raison et chercher la vérité dans les sciences de René Descartes, Beaugrand se montre plutôt favorable au correspondant de Mersenne. Il signe les privilèges d'édition de ces ouvrages après les avoir fait examiner par son ami Pierre de Fermat. Mais en conclusion de différentes polémiques, qui opposent Fermat et Descartes sur l'optique, la réfraction, et les moyens de trouver les tangentes à une courbe, la position de Beaugrand va se trouver profondément modifiée. Il conteste alors l'originalité de la géométrie analytique de Descartes et se plaint à Mersenne de ses plagiats. Dès mars 1638, il accuse Descartes d'avoir emprunté sa méthode à François Viète et au livre traduit de ce dernier, que lui-même lui avait offert en 1631. Cette polémique court jusqu'en 1640, date à laquelle il reproche encore à Descartes d'avoir emprunté également une grande partie de ses idées algébriques à Thomas Harriot. À cette occasion, il prend soin de montrer à Mersenne comment certaines propositions de Descartes ne sont que des copies des mêmes propositions chez Viète, à quelques changements de noms près. Ces accusations, qui sont encore l'objet de débats lui valent en retour de sévères critiques de Descartes.
À l'occasion d'une lettre à Mersenne (1538) apparaît sa façon de noter les puissances de l'indéterminée :
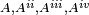
Dioptrique et méthode des tangentes
La polémique sur la Géostatique de Beaugrand se double courant 1637-1638 de celle opposant Fermat à Descartes, sur l'optique et sur la méthode d'obtention des tangentes.
- la querelle sur la Dioptrique
Il est probable que Mersenne ait demandé à Beaugrand de jouer de son influence à la cour en vue d'obtenir le privilège royal pour les œuvres de Descartes et que Jean de Beaugrand ait transmis le manuscrit de la dioptrique de Descartes à Fermat. Adrien Baillet donne une autre version de la communication de ce manuscrit ; selon lui, Beaugrand était l'un des plus curieux et des plus impatients à connaître les idées de Descartes. L'historien croit savoir que le secrétaire royal (Beaugrand) avait dépêché quelqu'un à Leyde pour lui envoyer les feuilles de la "Dioptrique" à mesure qu' on les imprimait. Il affirme que par ce moyen, Beaugrand se trouva pourvu d'un exemplaire avant même que Descartes n'eût eu la possibilité d'en faire tenir à ses amis du premier ordre.
Consulté par Mersenne, Fermat décèle dans cette dioptrique deux erreurs importantes. Il ne trouve pas convaincante « l'inclination au mouvement » par laquelle Descartes croit pouvoir expliquer les angles d'incidence des phénomènes de réfraction. Dans les raisons qu'il donne à ce que les milieux traversés ne s'opposent pas de la même façon au mouvement d'une balle et à celui de la lumière, Descartes commet une erreur logique puisqu'il prétend à la fois que le mouvement de la lumière est instantané et qu'elle va moins vite dans l'air que dans l'eau. En septembre 1637, Fermat rédige ses impressions à Mersenne. Il y relève la contradiction. Descartes, alerté, répond aussitôt à Mersenne :
« le défaut qu'il trouve en ma démonstration n'est qu'imaginaire et montre assez qu'il n'a regardé mon traité que de travers. [...] et si vous aviez envie par charité de le délivrer de la peine qu'il prend de rêver encore sur cette matière... »
La querelle qui s'en suit permet alors au protégé de Beaugrand (si Fermat le fut jamais) de montrer ses talents. Fermat a largement dépassé son mentor et fait montre à cette occasion de rigueur et de sang-froid :
« Ce n'est pas point par envie ni par émulation que je continue cette petite dispute, écrit-il à Mersenne, mais seulement pour découvrir la vérité; de quoi j'estime que M. Descartes ne me saura pas mauvais gré, d'autant plus que je connais son mérite très éminent, et que je vous en fais ici une déclaration très expresse. »
Pour autant, la querelle sur la dioptrique en reste là. Beaugrand signe le privilège d'impression des trois œuvres mathématiques de Descartes. Le 30 décembre 1637, il signe les lettres patentes nommant Pierre de Fermat conseiller aux enquêtes du parlement de Toulouse (Fermat sera installé le samedi 16 janvier suivant). Ce n'est qu'après la mort de Descartes, quinze ans plus tard, que le mathématicien de Beaumont parviendra à une formulation satisfaisante de son principe de durée minimale (Œuvres de Fermat, t. III, 149-156.)
- La méthode des tangentes
Alors que cette controverse s'éteint fin 1637, Descartes reçoit de Mersenne l'essai de Fermat intitulé Methodus ad disquirendam maximám et minimam. Aussitôt le philosophe reprend son « procès en mathématiques » contre monsieur Fermat. En janvier 1638, il écrit au père minime et s'étonne de ce que le toulousain l'ait défié. Il dénonce sa règle de formation des tangentes comme une resucée de la méthode dite de fausse position, il lui reproche de raisonner par l'absurde (méthode de raisonnement qui passe à ses yeux pour la façon de démontrer la moins estimée et la moins ingénieuse de toutes celles dont on se sert en Mathématiques). Il vante auprès du père minime sa propre méthode, tirée, selon ses mots, d'une connaissance de la nature des équations et qui suit, selon lui, la plus noble façon de démontrer qui puisse être…
Beaugrand publie alors un pamphlet pour défendre contre le S. des C. (sans mentionner les noms des protagonistes) les résultats de Fermat sur la détermination des tangentes. Il dénonce ceux, plus compliqués, de Descartes dont la méthode consiste à définir le cercle osculateur pour déterminer la tangente à partir de ce cercle.
Jean Itard lit dans ces publications la preuve de la supériorité de Pierre de Fermat dans la compréhension de la nature affine du problème des contacts. Selon ses mots, Fermat n'avait rien, ou presque, pour explique la nature affine de l'existence (et de la construction) des tangentes à une courbe ; car il ne s'agit pas d'un problème métrique. C'est pourtant ce qui le placera au-dessus de Descartes dans ce problème des tangentes où l'orthogonalité des axes de coordonnées n'est d'aucune importance. C'est ce que souligne Beaugrand dans son pamphlet anonyme.
En réalité Descartes a mal lu — ou mal compris — la méthode de Fermat, conclut dans son étude Michèle Grégoire ; le philosophe n'admettra d'ailleurs que du bout des lèvres l'excellence de cette méthode préfigurant le calcul différentiel de Leibniz
Le « géostaticien »
Dès mars 1638, Beaugrand reprend ses attaques contre Descartes, l'accusant devant Mersenne d'avoir plagié Viète. En juin 1638, Descartes, qui a fini par se désintéresser des questions mathématiques et s'est réconcilié avec Fermat, est sollicité par Mersenne pour donner son avis sur la Géostatique de Beaugrand. Il attaque alors Beaugrand sur son ouvrage, publié deux ans auparavant, et tourne la thèse de Beaugrand en ridicule. il assure au Minime avoir vu beaucoup de quadratures du cercle, de mouvements perpétuels, et d'autres telles démonstrations prétendues qui étaient fausses, mais qu'il n'avait jamais vu tant d'erreurs jointes ensemble en une seule proposition... Il conclut sa lettre par des mots très durs :
« Ainsi je puis dire pour conclusion que tout ce que contient ce livre de géostatique est si impertinent, si ridicule et si méprisable, que je m'étonne qu'aucuns honnestes gens ayent jamais daigné prendre la peine de le lire, et j'aurais honte de celle que j'ai prise d'en mettre ici mon sentiment, si je ne l'avais fait à votre semonce. »
Cette lettre, que lui montrera Mersenne, sera comme un coup de grâce pour le mathématicien et secrétaire royal. Le philosophe regrettera ultérieurement de s'être montré si cruel et réclamera de Mersenne de ne pas publier ces phrases, arguant qu’elles luy étoient échapées de la plume... mais la Géostatique de Beaugrand ne devait plus s'en relever.
Descartes, par mépris le traite de « géostaticien » (le surnom lui est resté dans les manuels d'histoire) et Beaugrand, piqué au vif, le qualifie en retour de « méthodique impertinent ». Aussi, Descartes va encore plus loin. En juin 1640, il fait du sobriquet de « géostaticien » une arme supplémentaire pour défendre sa géométrie analytique contre les tenants de l'algèbre nouvelle de Viète (dont Fermat), ramenant celle-ci à l'exégétique géométrique :
« Pour les retours Géométriques des questions trouvées par l’Algèbre, ils sont toujours si faciles, mais avec cela si longs et ennuyeux à écrire, quand les questions sont un peu belles, qu’ils ne méritent pas qu’un homme qui sait quelque chose s’y arrête, et c’est un emploi qui n’est bon que pour le « géostaticien » ou ses semblables. »
— René Descartes, lettre du 11 juin
La réponse de Beaugrand parvint à Mersenne sous forme de trois lettres, redécouvertes à la fin du XIXe siècle par Paul Tannery où il demande que Descartes reconnaisse ce qu'il a emprunté à Viète. Son dessein n'étant pas que le père Minime transmette ses critiques au Philosophe de la Haye, Beaugrand s'y montre déçu d'apprendre que Mersenne a communiqué ses remarques en Hollande. Comme, selon ses mots, Beaugrand n'a rien avancé que de très véritable, il l'informe de ses principaux chefs d'ccusation,
« Qu'autant que de lui donner l'absolution de son crime, ajoute-t-il, vous l'obligerez a restituer ou du moins a reconnaître ce qu'il s'est voulu injustement attribuer. »
Il détaille plus loin les emprunts qu'il reproche au philosophe :
D'après Beaugrand, ce que dit Descartes pour augmenter, diminuer, multiplier ou diviser les racines d'une équation sans les connaître, est tiré du chapitre De generali methodo transmutandarum equationum, édité par lui même (en 1631) et Anderson dès 1617 ; livre dans lequel François Viète apprend à déformer une équation sans apporter aucun changement à la quantité inconnue, ou en la changeant de telle sorte que la nouvelle quantité inconnue ait un rapport connu a la précédente, c'est-à-dire de façon fonctionnelle (Beaugrand l'exprime en disant que l'on ne peut trouver les valeurs de l'une sans en pouvoir déduire les valeurs de l'autre). Plus loin, il reproche au philosophe de la Haye sa règle pour ôter le second terme d'une équation. Selon le secrétaire royal, celle-ci dérive du chapitre De expurgatione per uncias, donnée par le même Alexander Anderson, où cette règle est amplement expliquée et démontrée ; il sous-entend d'ailleurs que Descartes ne l'a pas entendu entièrement... Enfin, il s'attaque à sa règle pour réduire les nombres rompus d'une équation à des entiers, (c'est à dire passer de la recherche de solutions rationnelles à la recherche de solutions entières par la formation d'un polynôme homogène) règle qui selon Beaugrand est déjà expliqué, et beaucoup plus généralement qu'il n'a fait, dans le chapitre De Isomeria adversus vitium fractionis (et donc une fois encore, déduite de François Viète).
Il ajoute qu'on aurait eu de l'obligation au S[ieur] Desc[artes], s'il eût inventé par sa méthode, les belles choses qui étaient dans l'œuvre de Viète mais aussitôt, il affirme que la seule obligation où il se voit réduit est de l'accuser d'avoir déguisé ses emprunts supposés, qu'il nomme des larcins :
« A n'en point mentir, conclut-t-il ce n'est pas seulement aux dépens de M. Viète. qu'il (Descartes) a voulu paraître habile homme ; je vous ferai, par vous même, voir une autre fois, qu'il a pris en plusieurs autres auteurs (Thomas Harriot) ce qu'il a trouvé a l'écart, croyant qu'il n'y aurait personne qui eût assez de lecture, ni la vue assez subtile pour s'en apercevoir. »
Ces accusations, reprises par John Wallis, puis l'école anglaise, se heurte à une fin de recevoir de la part de Descartes, qui affirme solennellement au père Mersenne n'avoir jamais touché la couverture d'un ouvrage de François Viète avant son départ de France. Tannery et Adam assure pour leur part que Descartes connaissait au moins l'opuscule édité en 1631 par Beaugrand ; puisque Mersenne le lui envoya, et qu'il en accusa réception, mettant même l'éditeur au défi de résoudre le problème de Pappus, ajoutent-ils
Derniers feux
Le 1er juin 1639, Beaugrand observe le passage d'une comète avec Roberval, Claude Hardy, Mydorge, Étienne Pascal et Bouillaud. Cette année-là et en 1640, il écrit deux dernières lettres contre Girard Desargues afin de défendre la géométrie classique, l'une d'elle sera publiée, à titre posthume, en 1642. Beaugrand y démontre les résultats de Désargues par un appel au théorème de Menelaus, sans user des arguments de géométrie projective de son concurrent.
Un autre opposant à Descartes, Didier Dounod de Bar le duc, étant mort la même année, « Je prie Dieu pour leurs âmes à tous deux », répondit le philosophe de la Haye, lorsque Mersenne lui en annonça la nouvelle.
Outre Fermat, Roberval, Pascal, Hardy et Herigone, Beaugrand était lié avec Jean-François Niceron. Ce dernier transmet quelques unes des dernières inventions de Beaugrand à Bonaventura Cavalieri. À l'annonce de sa mort, l'Italien écrit :
« Je lui [Niceron] fit part de ma découverte et de retour à Paris, il lui plut de communiquer la susdite progression et la mesure du fuseau parabolique à l'illustre Jean de Beaugrand, que je connaissais déjà... Mais par une lettre du père Mersenne, j'appris inopinément le décès du dit Beaugrand... Je m'affligeais beaucoup de la perte d'un si grand homme. »























































