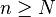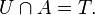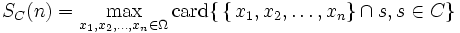Pulvérisation - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le terme de pulvérisation a été introduit en 1975 par J. M. Steele dans sa thèse de doctorat, à l'université Stanford.
Le concept de pulvérisation d'un ensemble de points joue un rôle important dans la théorie de Vapnik-Chervonenkis, également connue sous le nom de théorie VC. La pulvérisation et la théorie VC sont utilisées dans l'étude des processus empiriques ainsi qu'en théorie de l'apprentissage automatique statistique.
Définition
Soient C une classe d'ensembles et A un ensemble. On dit que C pulvérise A si et seulement si, pour tout sous-ensemble T de A, il existe un élément U appartenant à C tel que
Ceci équivaut encore à dire que C pulvérise A si et seulement si l'ensemble des parties de l'ensemble A, P(A), est égal à l'ensemble { U ∩ A | U ∈ C }.
Par exemple, la classe C des disques du plan (lorsqu'on se place dans un espace à deux dimensions) ne peut pas pulvériser tous les ensembles F de quatre points, alors qu'en revanche la classe des ensembles convexes du plan pulvérise tout ensemble fini du cercle unité.
classe de Vapnik-Chervonenkis
La dimension VC d'une classe C est définie par
- VC(C) = minn{n:SC(n) < 2n} ou, de manière alternative, par : VC0(C) = maxn{n:SC(n) = 2n}
On remarquera qu'on a : VC(C) = VC0(C) + 1.
On dira que la dimension VC d'une classe est infinie si pour tout n il existe un ensemble à n éléments pulvérisé par C (on a alors, pour tout entier naturel n, SC(n) = 2n).
Les classes de dimension VC finie sont appelées classes de Vapnik-Chervonenkis ou classes VC. Une classe d'ensembles est une classe uniformément Glivenko-Cantelli si et seulement si c'est une classe VC.
Coefficient de pulvérisation
Pour mesurer la richesse d'une collection C d'ensembles, on utilise le concept de coefficients de pulvérisation (également appelés fonction de croissance). Pour une collection C d'ensembles
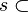
où "card" signifie cardinal, c'est-à-dire, le nombre d'éléments d'un ensemble.
De cette définition découlent les propriétés suivantes :
- 1.
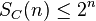
- 2. SC(n) = 2n, si et seulement s'il existe un ensemble de cardinal n pulvérisé par C.
- 3. S'il existe N > 1 tel que SC(N) < 2N, alors SC(n) < 2n pour tout