Régression logistique - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Notations, hypothèses et estimations - Évaluation statistique de la régression - Matrice de confusion - Évaluation d'un bloc de coefficients - Évaluation individuelle des coefficients - Lecture des résultats - Autres évaluations - Redressement - Déploiement

Évaluation statistique de la régression

Il est possible d’exploiter un schéma probabiliste pour effectuer des tests d’hypothèses sur la validité du modèle. Ces tests reposent sur la distribution asymptotique des estimateurs du maximum de vraisemblance.

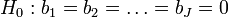
Pour vérifier la significativité globale du modèle, nous pouvons introduire un test analogue à l’évaluation de la régression linéaire multiple. L’hypothèse nulle s’écrit $H_0 : b_1 = b_2 = \dots = b_J = 0$ , que l’on oppose à l’hypothèse alternative $H 1$ : un des coefficients au moins est non nul

La statistique du rapport de vraisemblance s’écrit $\Lambda = 2 \times [l(J+1)-l(1)]$ , elle suit une loi du $χ 2$ à $J$ degrés de libertés.

$l (J + 1)$ est le logarithme de la vraisemblance du modèle avec l’ensemble des variables (donc J+1 coefficients en comptant la constante) et,
$l (1)$ la log vraisemblance du modèle réduit à la seule constante.

Si la probabilité critique (la p-value) est inférieure au niveau de signification que l’on s’est fixé, on peut considérer que le modèle est globalement significatif. Reste à savoir quelles sont les variables qui jouent réellement un rôle dans cette relation.

Matrice de confusion

L’objectif étant de produire un modèle permettant de prédire avec le plus de précision possible les valeurs prises par une variable catégorielle $Y$ , une approche privilégiée pour évaluer la qualité du modèle serait de confronter les valeurs prédites avec les vraies valeurs prises par $Y$ : c’est le rôle de la matrice de confusion. On en déduit alors un indicateur simple, le taux d’erreur ou le taux de mauvais classement, qui est le rapport entre le nombre de mauvaises prédictions et la taille de l’échantillon.

Lorsque la matrice de confusion est construite sur les données qui ont servi à élaborer le modèle, le taux d’erreur est souvent trop optimiste, ne reflétant pas les performances réelles du modèle dans la population. Pour que l’évaluation ne soit pas biaisée, il est conseillé de construire cette matrice sur un échantillon à part, dit échantillon de test. Par opposition à l’échantillon d’apprentissage, il n’aura pas participé à la construction du modèle.

Le principal intérêt de cette méthode est qu’elle permet de comparer n’importe quelle méthode de classement et sélectionner ainsi celle qui s’avère être la plus performante face à un problème donné.

Évaluation d'un bloc de coefficients

Les deux tests ci-dessus sont des cas particuliers du test de significativité d’un bloc de coefficients. Ils découlent du critère de la « déviance » qui compare la vraisemblance entre le modèle courant et le modèle saturé (le modèle dans lequel nous avons tous les paramètres).

L’hypothèse nulle s’écrit dans ce cas $H 0 :β(q) = 0$ , où $β(q)$ représente un ensemble de $q\,$ coefficients simultanément à zéro.

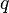
La statistique du test $W(q) = 2 \times [l(J+1)-l(J+1-q)]$ suit une loi du $χ 2$ à $q$ degrés de libertés.

Ce test peut être très utile lorsque nous voulons tester le rôle d’une variable explicative catégorielle à $q + 1$ modalités dans le modèle. Après recodage, nous introduisons effectivement $q$ variables indicatrices dans le modèle. Pour évaluer le rôle de la variable catégorielle prise dans son ensemble, quelle que soit la modalité considérée, nous devons tester simultanément les coefficients associés aux variables indicatrices.

Évaluation individuelle des coefficients

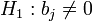
Dans le cas où l’on cherche à tester le rôle significatif d’une variable. Nous réalisons le test suivant $H 0 : b j = 0$ , contre $H_1 : b_j \ne 0$ .

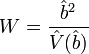
La statistique de WALD répond à ce test, elle s’écrit $W = \frac{\hat b^2}{\hat V(\hat b)}$ , elle suit une loi du $χ 2$ à $1$ degré de liberté.