Somme de Minkowski - Définition
La liste des auteurs de cet article est disponible ici.
Inégalité de Brunn-Minkowski
L'égalité de Brunn-Minkowski est une majoration du volume de la somme de deux parties mesurables d'un espace euclidien :
-
- Soient E un espace euclidien de dimension n, μ la mesure de Lebesgue sur E et A et B deux compacts non vides de E. La majoration suivante, appelée inégalité de Brunn-Minkowski est vérifiée :
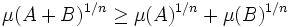
La majoration est illustrée sur la figure de droite. Elle représente la somme d'un hexagone jaune et d'un disque vert. La mesure de la somme est toujours supérieure à la somme des mesures. Sur la figure, l'excédent C est représenté en bleu, la mesure de cet excédent vérifie la majoration suivante :
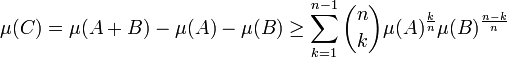
La majoration est une égalité si, et seulement si, A et B sont deux figures homothétiques.
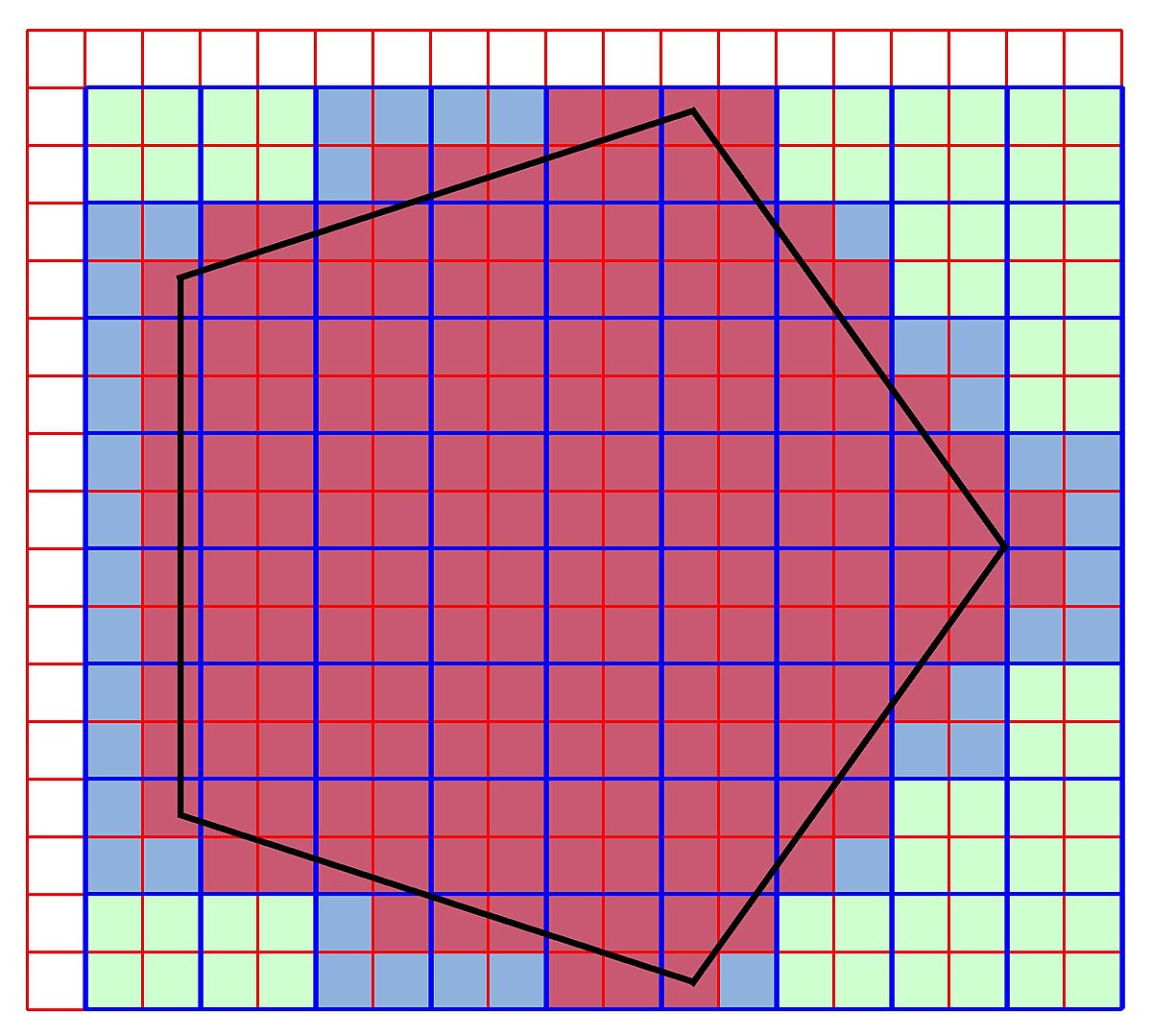
L'espace E est équipé d'une base orthonormale, puis il est quadrillé par une grille composée d'hyperplans dont les directions sont orthogonales à un des vecteurs de la base. Ces hyperplans sont régulièrement espacés, avec un pas de 1/2p, ou p est un entier strictement positif. Cette grille pave l'espace à l'aide de petits hypercubes d'arêtes de longueur 1/2p. La mesure de Lebesgue choisie est celle qui associe à un hypercube de côté de longueur 1 la valeur 1.
Ces hypercubes permettent d'approximer un compact. Par exemple, sur la figure de droite un pentagone régulier est approximé par des carrés bleus. Affiner la grille revient à choisir une valeur plus élevée pour p. La figure de droite illustre aussi une deuxième approximation par des petits carrés rouges obtenu pour un incrément de 1 de la valeur p. L'article Distance de Hausdorff montre que cette technique permet de construire une suite (An) de compacts contenant A et approximant de plus en plus précisément A, au sens de la distance de Hausdorff.
La démonstration proposée ici se déroule en trois temps. Dans un premier temps, on la démontre dans le cas où A est un hypercube de la grille et B un hypercube inclus dans un de ceux de la grille et dont les arêtes sont toutes de longueur a = 1/2p sauf celles parallèles au premier vecteur de la base qui sont de longueur λ.a. Ici, λ désigne un nombre réel strictement positif et plus petit que 1.
-
-
- Dans le cas où A et B sont deux hypercubes décrits ci-dessus, la majoration de Brunn-Minkowski est vérifiée :
-
- Le cas est suffisamment simple pour permettre un calcul effectif des trois mesures.
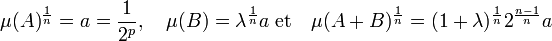
- Démontrer la majoration dans le cas présent revient à montrer que la fonction f de ]0,1] dans R, où R désigne l'ensemble des nombres réels, est strictement positif, sur ]0,1[ et nulle en 1.
![\forall t \in ]0,1]\quad f(t) = (1+ \lambda)^{\frac 1n}2^{\frac {n-1}n} - \lambda^{\frac 1n} - 1\;](https://static.techno-science.net/illustration/Definitions/autres/2/2097bb5622130ee2eff7fe5aa41e3bbe_47baa235212cd3209aceefd4be06d773.png)
- Il est clair que la fonction f est nulle au point 1, il suffit de montrer qu'elle est strictement décroissante pour conclure. La fonction f est dérivable sur ]0,1[, il suffit de montrer que sa dérivée est strictement négative, ce qui se vérifie aisément.
![\forall t \in ]0,1[ \quad f'(t) = \frac 1n \left(\left(\frac 2{1 + \lambda}\right)^{\frac {n-1}n} - \left(\frac 1{\lambda}\right)^{\frac {n-1}n}\right) = \frac 1{n\lambda^{\frac {n-1}n}} \left(\left(\frac {2\lambda}{1 + \lambda}\right)^{\frac {n-1}n} - 1\right)<0](https://static.techno-science.net/illustration/Definitions/autres/6/679c858d687622d89fded536866b1393_75e15305688815f88e58c078c4185bf5.png)
On suppose maintenant que A et B sont deux unions finies d'intérieurs d'hypercubes de la grille ou de partie d'hypercubes ouverts dont une des coordonnées est comprise entre 1/2p.(δ + λ) et 1/2p.(δ + 1). C'est-à-dire que les hypercubes sont du type de la proposition précédente. Les valeurs q et r désignent le nombre d'hypercubes composant respectivement A et B.
-
-
- Dans le cas où A et B sont deux compacts de la forme décrite ci-dessus, la majoration de Brunn-Minkowski est vérifiée :
-
- On raisonne par récurrence sur l'entier s égal à la somme de q et de r. Si s est égal à 2, le résultat est une conséquence directe de la proposition précédente.
- On suppose le résultat établi jusqu'à une valeur s0 et on suppose que la somme de q et de r est égale à s0 + 1. On sépare l'espace euclidien E en deux connexes par un des hyperplans HA orthogonal à l'un des vecteurs de la base orthonormale qui définit la grille. Il existe un hyperplan de cette nature qui décompose A en deux ouverts disjoints A1 et A2 tel que A2 comporte au moins un hypercube et tel que A1 ne soit pas l'ensemble vide. A1 et A2 sont alors composés d'au plus de q - 1 hypercubes. On note θ le nombre réel strictement positif suivant :
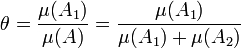
- On sépare B en deux ensembles B1 et B2 par un hyperplan HB parallèle au précédent, de telle manière à ce que :
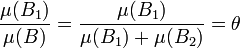
- Ni B1 et B2 ne contiennent de vecteurs de l'hyperplan HB, en conséquence, B contient mais n'est pas nécessairement égal à l'union de B1 et B2, mais comme un sous ensemble inclus dans un hyperplan est de mesure nulle, l'égalité précédente est vérifiée. Cette fois ci, rien ne prouve que B1 et B2 contiennent moins d'hypercubes que B, mais il est certain qu'ils n'en contiennent pas plus. Les propriétés de la somme de Minkowski montrent que :
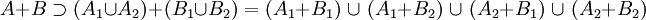
- Considérons le vecteur de la base orthonormale orthogonale aux deux hyperplans HA et HB, les coordonnées sur ce vecteur de tout élément de A1 + B1 sont strictement plus petites que celles des vecteurs de A2 + B2, ce qui montre que les deux ensembles sont disjoints et :
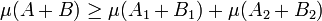
- Comme A1 et A2 contiennent strictement moins que q petits hypercubes et que B1 et B2 n'en contiennent pas plus que r, il est possible d'appliquer l'hypothèse de récurrence :
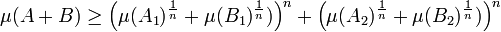
- Ce que l'on peut encore écrire :
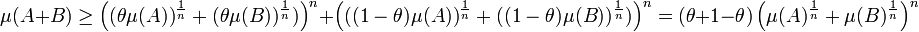
- Ce qui montre la majoration qui termine la démonstration :
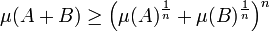
Il est maintenant possible de prouver la majoration de Brunn-Minkowski dans le cas général. On utilise pour cela un passage à la limite utilisant la distance de Hausdorff. Soit ε un réel strictement positif et A et B deux compacts de E. L'objectif de la démonstration est de montrer que la somme de la mesure de A + B et de ε majore bien le deuxième membre de l'inégalité. On utilise trois propriétés démontrées dans l'article Distance de Hausdorff.
-
-
- Si A et B sont deux compacts non vides, l'inégalité de Brunn-Minkowski est vérifiée :
-
- Dans un premier temps, on utilise la semi-continuité supérieure de la fonction mesure pour la distance de Hausdorff. Si EH désigne l'ensemble des compacts non vides de E et d la distance de Hausdorff :

- Il s'agit maintenant de construire le bon ensemble C. On utilise l'existence de deux ensembles Aε et Bε compacts contenant strictement A et B et tel que :
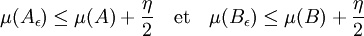
- Les deux ensembles Aε et Bε sont des unions finies d'hypercubes fermés de la grille, pour une valeur de p suffisamment élevée. L'existence de tels ensembles provient du fait que les unions finies d'hypercubes fermés pris dans la grille forment un ensemble dense si p décrit les entiers positifs. La démonstration de la continuité de la somme de Minkowski pour la distance de Hausdorff (cf l'article Distance de Hausdorff) montre que :
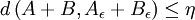
- On choisit C égal à la somme de Aε et Bε, ce qui montre que :

- On retire à l'ensemble Aε + Bε son intersection avec les hyperplans de la grille, ce qui ne modifie pas sa mesure. On se trouve alors dans les hypothèses de la proposition précédente et :

- Ici, Aoε et Boε désignent les ensembles Aε et Bε otés de leurs intersections avec les hyperplans de la grille. Rajouter cette intersection ne modifie en rien les mesures, ce qui montre que :

- Par hypothèse, les ensembles Aε et Bε contiennent A et B. Leur mesure est plus grande, et :

- Cette majoration est vraie pour toute valeur de ε strictement positive, ce qui montre le résultat cherché.