Somme de Minkowski - Définition
La liste des auteurs de cet article est disponible ici.
Formule de Steiner-Minkowski
Dimension 2
La formule de Steiner a été découverte pour démontrer le théorème isopérimétrique. En dimension 2, il stipule que si C est une surface de périmètre p, alors son aire est plus petite que celle du disque de périmètre p. Si le périmètre p n'est pas fini, comme par exemple pour un compact construit à l'aide d'une courbe de Koch, la formule reste exacte, mais ne possède plus aucun intérêt. Le théorème prend la forme suivante :
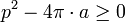
L'égalité n'étant obtenue que dans le cas ou le compact C est un disque.
Pour le démontrer, une approche consiste à étudier l'aire de la somme de Minkowski d'un convexe compact C et de t.B, où t désigne un réel positif et B le disque unité, de centre le vecteur nul et de rayon 1. On trouve l'égalité suivante, si μ est la fonction volume qui à C associe son aire, et C est un ensemble convexe :
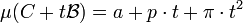
La fonction volume μ est définie de manière très générale, elle correspond à la mesure de Lebesgue, qui à un carré de côté 1 associe 1. Le périmètre d'une courbe est définie à la manière de Jordan, c'est-à-dire qu'il est égal à la borne supérieure des longueurs de lignes polygonales approximant la frontière. Sous cette forme, démontrer le théorème isopérimétrique revient à montrer que le polynôme du second degré, qui à t associe μ(C + t.B), possède un discriminant positif, ou encore que le polynôme admet une racine réelle.
Cette formule permet aussi d'obtenir une expression du périmètre p, toujours si C est convexe en fonction de la fonction φ:

Dimension quelconque
Il est tentant de généraliser la formule, dans un espace euclidien E de dimension n. On peut considérer la mesure du volume s.C1 + tC2, où C1 et C2 sont deux compacts convexes et s et t deux réels positifs. On obtient une expression polynomiale du type :
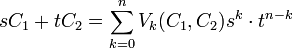
Les coefficients ak s'appellent volumes mixtes de C1 et C2.
On dispose de quelques égalités évidentes :
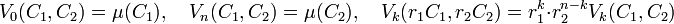
Une autre est un peu plus délicate à démontrer dans le cas où C2 est égal à B :
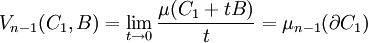
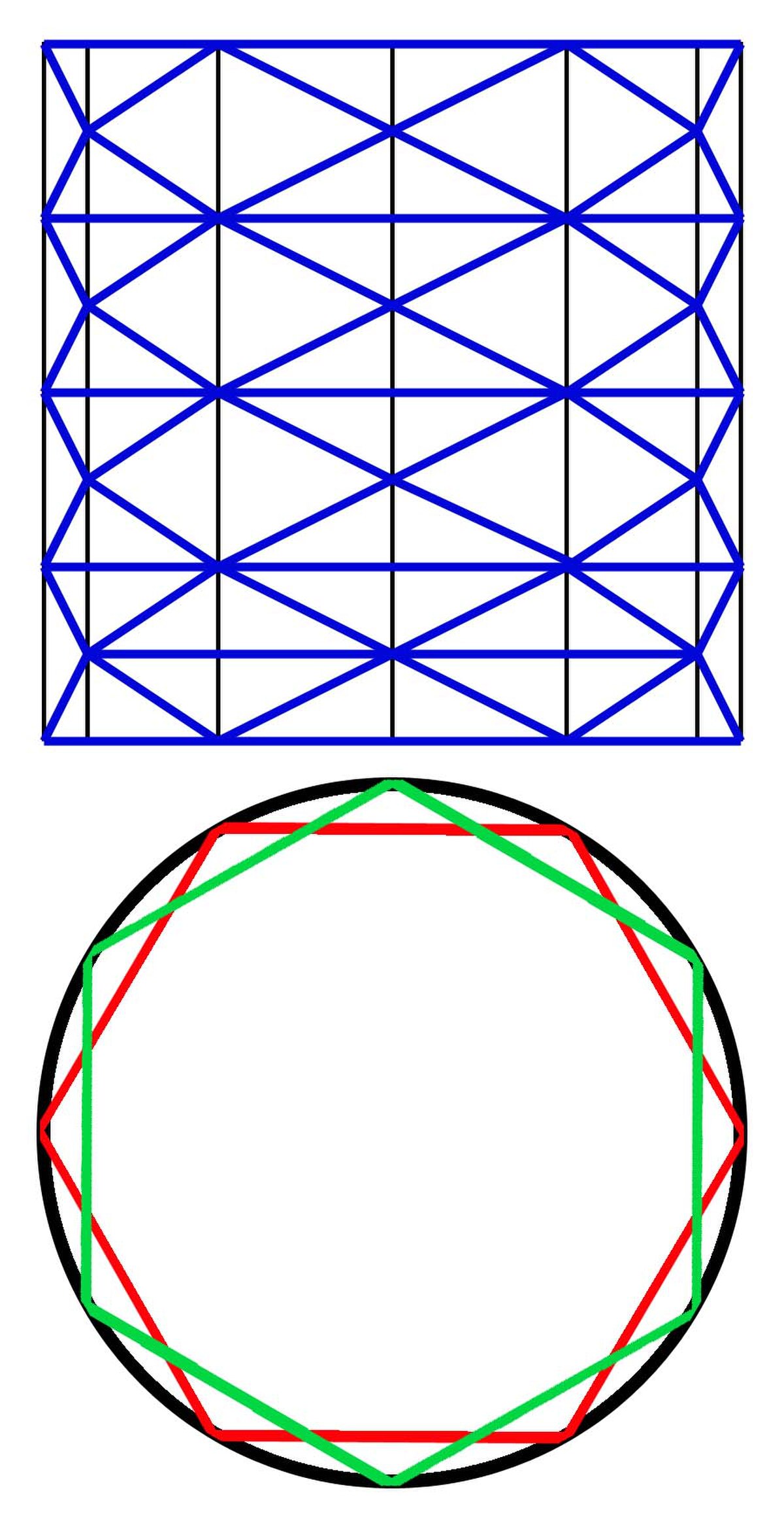
Ici, μn-1 désigne le volume n - 1 dimensionnel. Définir une mesure n - 1 dimensionnelle devient subtil. Une première méthode consiste à généraliser la technique utilisée en dimension 1, pour un arc rectifiable. Elle demande d'être adaptée et est spécifique aux convexes. La mesure de la surface est alors la borne supérieure des convexes polyédriques inclus dans C1. La convexité est indispensable, sinon le contre exemple de droite montre que la définition ne fait pas sens. La surface que l'on souhaite mesurer est un cylindre, le polyèdre utilisé est un lampion dont les sommets sont situés sur des hexagones chaque fois décalés d'un douzième de tour. Si les plans des hexagones se rapprochent de plus en plus, la surface du polyèdre augmente jusqu'à l'infini. Une autre technique consiste à utiliser une forme différentielle et plus précisément une forme volume. La difficulté réside alors dans le fait que la surface d'un convexe n'a pas de raison d'être une variété de classe C1. Il devient nécessaire d'utiliser des espaces comparables à ceux de Sobolev pour définir la surface.
Les volumes mixtes vérifient une majoration utilisée pour démontrer le théorème isopérimétrique pour les dimensions supérieures à 2. Elle porte le nom d'inégalité de Alexandrov-Fenchel :
![\forall i \in [1, n-1]\quad V_k(C_1,C_2)^2 \le V_{k-1}(C_1,C_2)\cdot V_{k+1}(C_1,C_2)](https://static.techno-science.net/illustration/Definitions/autres/9/9f4ea077bea91248f68dd08826539b85_e3a6fec82f6d890840078f11fa5327c2.png)
Ici, E désigne un espace euclidien de dimension n.
-
- Si P est un polyèdre compact et convexe de E, la fonction qui à (s, t) associe la mesure μ(s.P + t.B) est un polynôme homogène de degré n :
Notons M cette mesure. M est la somme de la mesure μ(s.P) et de la croute ajoutée par la somme de t.B. Le terme associé à la mesure de μ(s.P) est une constante que multiplie sn.
Sur chaque face, on trouve un hypercube Hi1 de dimension n, de base la face en question et de hauteur t de dimension n - 1 et de mesure le produit d'une constante et de sn-1. Chacune de ces faces contribue au volume μ(P + t.B) sous la forme d'une expression linéaire en sn-1.t.
Entre ces hypercubes, on trouve des interstices Hj2, ayant la forme d'un prisme, d'arête l'intersection de deux faces, et de dimension n - 2, dont la mesure est le produit d'une constante avec sn-2 et de côtés deux faces d'hypercubes Hi1 ayant une arête de longueur t, le sommet un composé du produit d'un disque de rayon t et d'un hypercube isomorphe à l'arête. Ces prismes sont donc des portions de cylindre d'axe un hypercube de dimension n - 2 et de rayon r. Chacune de ces portions de cylindre contribue au volume μ(P + t.B) sous la forme d'une expression en sn-2.t2.
Les arêtes de dimension n - 2 ont comme extrémités des hypercubes de dimension n - 3 qui laissent place à des interstices, laissée vacant par les solides Hi1 et Hj2. Ces interstices Hk
On continue ainsi jusqu'à la dimension 1, l'intersection des arêtes est alors de dimension 0 et correspond à un point. L'interstice correspond à une portion de boule, dont l'expression est le produit d'une constante par tn.
Le terme en sn correspond à la mesure de P, celui en sn-1.t à la mesure de la surface de P. Si s est égal à 0, on remarque que le volume est celui d'une boule de rayon t, la constante est celle associée au volume n dimensionnel d'une sphère.
-
- Si C est un compact, convexe non vide de E, la fonction qui à (s, t) associe la mesure μ(s.C + t.B) est un polynôme homogène de degré n :
Soit (Cp) une suite décroissante de polyèdres convexes dont la limite, au sens de Hausdorff, est égale à C. Le paragraphe ensemble dense de l'article Distance de Hausdorff montre qu'une telle suite existe. Soit Pp(s, t) le polynôme homogène de degré n qui à (s, t) associe μ(s.Cp + t.B), l'objectif est de montrer que la suite (Pp) converge simplement.
La suite (s.Cp + t.B) est une suite de compacts, décroissante pour l'inclusion, elle est nécessairement convergente au sens de Hausdorff, montrons que la limite est égale à s.C + t.B. Tout ensemble de la suite contient s.C + t.B, la limite contient donc cet ensemble. Réciproquement si y n'est pas élément de s.C + t.B, il existe un nombre réel strictement positif ε tel que la boule de centre y et de rayon ε ait une intersection nulle avec s.C + t.B car cet ensemble est fermé. On en déduit que tout élément de s.Cn est à une distance supérieure à t + ε de y. Si s n'est pas nul, cela signifie aussi que y est à une distance supérieure à (t + ε)/s de C. A partir d'un certain N, pour toute valeur de p plus grande que N, Cp est à une distance de y strictement supérieure à t/s, et s.Cp + t.B ne peut contenir y. Si s est nul, la suite s.Cp + t.B est constante égale à t.B et est trivialement convergente.
Comme la suite (s.Cp + t.B) est une suite de compacts strictement décroissante, de limite s.C + t.B, et que la fonction μ est semi-continue supérieurement, la suite μ(s.Cp + t.B) est convergente (cf le paragraphe Fonctions continues de l'article Distance de Hausdorff). Ce qui signifie exactement que la suite (Pp) converge simplement.
Chaque polynôme de la suite (Pp) est un polynôme homogène de degré n, cette suite fait partie de l' espace vectoriel des polynômes à deux variables de degré inférieur à n et est de dimension finie. Sur cet espace, la topologie de la convergence simple est compatible avec l'addition et la multiplication externe, ce qui signifie que ces deux opérations sont continues. Or, sur un espace vectoriel réel de dimension finie, il n'existe qu'une topologie compatible avec ses deux opérations, (cf topologie d'un espace vectoriel de dimension finie). Cette topologie est induite par n'importe quelle norme, par exemple celle de la convergence uniforme sur le disque de rayon r, où r désigne un nombre réel strictement positif. L'espace vectoriel des polynômes à deux variables homogènes et de degré n est complet pour cette norme, ce qui montre que la suite (Pp) converge vers un polynôme P homogène de degré n.
Cette limite P est, par construction, la fonction qui à (s, t) associe μ(s.C + t.B), ce qui démontre la proposition.