Somme de contrôle - Définition

Somme de contrôle et cryptographie

Une somme de contrôle est utile pour détecter des modifications accidentelles des données, mais n'a pas vocation à assurer une protection contre les modifications intentionnelles. Plus précisément, elle ne peut en général pas assurer directement l'intégrité cryptographique des données. Pour éviter de telles modifications, il est possible d'utiliser une fonction de hachage adaptée, comme SHA-256, couplée à un élément secret (clé secrète), ce qui correspond au principe du HMAC.

Formalisation

Code linéaire

L'objectif est la transmission d'un message m, c’est-à-dire d'une suite de longueur k de lettres choisies dans un alphabet. Le message apparaît comme un élément d'un ensemble S_k. L'objectif est de transmettre un code c tel que le récepteur soit capable de détecter l'existence d'altérations si le nombre d'erreurs ne dépasse pas un entier t. Un code est la donnée d'une application φ de S_k dans un ensemble E qui à m associe φ(m) = c. L'application φ est une injection, car sinon deux messages distincts auraient le même code et le récepteur ne saurait les distinguer.

Le bit de parité procède de la famille des codes linéaires. Cette méthode consiste à munir les ensembles S_k et E d'une structure algébrique adaptée pour bénéficier de bonnes propriétés. L'alphabet K est choisi muni d'une structure de corps fini. En général il est égal à {0,1} le corps à deux éléments. S_k et E sont des K espace vectoriel. L'application φ est linéaire. L'ensemble des messages reçus sans erreurs est égal à φ(S_k), un sous-espace vectoriel de E appelé code.

Poids de Hamming

Code de longueur deux avec un bit de parité

La transmission est sujet à des altérations, en conséquence le récepteur ne reçoit pas toujours le code c = φ(m) mais parfois φ(m) + e où e est la conséquence de la mauvaise transmission. Par hypothèse, e contient moins de t coordonnées non nulles. Le nombre de coordonnées non nulles d'un vecteur de E est appelé poids de Hamming et le nombre de coordonnées qui diffèrent entre c et c + e est la distance de Hamming. C'est une distance au sens mathématique du terme.

Si tous les points du code φ(S_k) sont à une distance strictement supérieure à t les uns des autres, alors c + e n'est pas un élément du code, le récepteur sait donc que le message est erroné et il est en mesure de demander une nouvelle transmission.

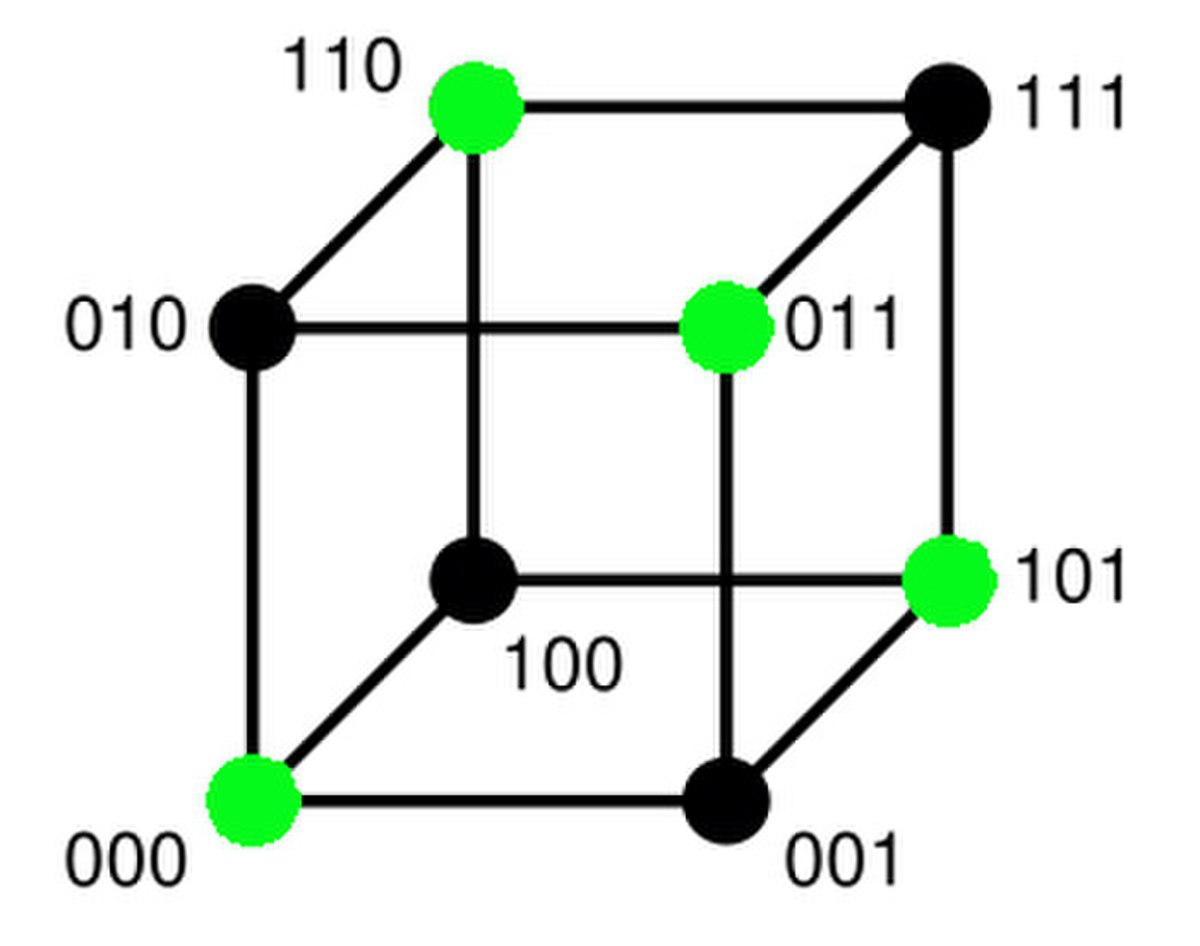
La figure de droite illustre cette situation. k est égal à deux, le corps K est égal à {0,1} et t est égal à 1. S_k = {00, 01, 10, 11} est un espace vectoriel de dimension deux. E est l'espace vectoriel K³, illustré sur la figure. L'application φ associe à un message m, le vecteur de coordonnés celle de m et la somme dans K des deux coordonnées de m. Dans le corps K l'égalité 1 + 1 = 0 est vérifiée. On a donc :

Le code, c’est-à-dire φ(S_k) est représenté par les points verts sur la figure. Les points à distance de 1 d'un point vert sont ceux obtenus par un déplacement sur un unique segment du cube. Ils sont tous noirs, c’est-à-dire qu’ils ne font pas partie du code et sont donc nécessairement erronés. Si une unique altération se produit, alors le récepteur sait que la transmission a été mauvaise.

Un code linéaire est décrit par trois paramètres, noté [k, n, d]. La première valeur k est la longueur du code, c’est-à-dire le nombre de lettres d'un message, n est la dimension du code, correspondant à la dimension de l'espace vectoriel E et d est la distance minimale entre deux mots du code. Un code est dit parfait s'il existe un entier t tel que les boules de centre un élément du code et de rayon t forment une partition de E.

Propriétés

La théorie des corps finis permet de démontrer deux propriétés essentielles sur l'utilisation d'une unique somme de contrôle dans un code.

• Soit K un corps fini et k un entier strictement positif. Il existe un code sur le corps K de paramètre [k+ 1, k, 2] composé de l'identité et d'une somme de contrôle.

Ce type de code est le plus compact à même de détecter une erreur de poids un. En effet, un code plus petit aurait une dimension égale à k et donc aucune redondance. il est MDS, car il atteint la borne de Singleton. C’est-à-dire que sa dimension moins sa longueur est égale à sa distance minimale moins un. En revanche, le code n'est pas parfait, c’est-à-dire que les boules de centres les mots du code et de rayon un ne forment pas une partition de E, un point extérieur au code est en général à une distance de un de plusieurs points du code, il appartient donc à plusieurs boules.

• Soit K un corps fini et k un entier strictement positif. Tout code sur le corps K de paramètre [k + 1, k, 2] est isomorphe à un code composée de l'identité et d'une somme de contrôle.

En d'autres termes, si un code MDS est de distance minimale égale à deux, alors il est construit à l'aide de l'identité et d'une somme de contrôle. La somme de contrôle est donc l'unique manière optimale de détecter une altération.

• Soit K un corps fini et k un entier strictement positif. Il existe un code sur le corps K de paramètre [k + 1, k, 2] composé l'identité et d'une somme de contrôle.

Considérons le code de matrice génératrice (cf le paragraphe Définitions de l'article Code linéaire) c’est-à-dire dont la matrice G de k lignes et k + 1 colonnes, dans les bases canoniques est la suivante:

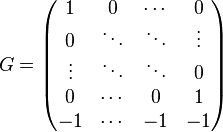
La matrice est bien construite à l'aide de la matrice identité et de la somme de contrôle. Par construction, les deux premiers paramètres du code sont bien k et k + 1. L'endomorphisme φ est bien injectif car sa matrice contient une sous-matrice identité de dimension k.

Il ne reste plus qu'à montrer que si m et m' sont deux messages distincts, alors la distance de Hamming entre φ(m) et φ(m') est bien supérieure ou égal à deux. Ceci revient à montrer que si a est le message égal m - m' alors φ(a) possède un poids de Hamming supérieur ou égal à deux. On remarque qu'il existe des éléments du code φ(S_k) dont le poids est égal à deux, par exemple l'image de n'importe quel élément de la base de S_k. Il suffit donc de montrer que tout vecteur ayant une unique coordonnée non nulle n'est pas élément du code. C’est-à-dire qu'aucun vecteur de la base de E n'est élément de φ(S_k).

Soit (f_j) où j est un entier compris entre 1 et k + 1 la base canonique de E. Si f _{k + 1} est élément du code, alors comme f_j - f _{k + 1} est élément du code si j est inférieur ou égal à k, f_j est aussi élément du code. Le code contiendrait donc les k + 1 vecteur de la base de E. Or le code est de dimension k, en conclusion f _{k + 1} n'est pas élément du code. Si f_j est élément du code avec j inférieur ou égal à k, alors f _{k + 1} est aussi élément du code car f_j - f _{k + 1} l'est, or c'est impossible d'après l'analyse précédente. La distance minimale est donc bien égale à deux.

• Tout code sur le corps K de paramètre [k + 1, k, 2] est isomorphe à un code composée de l'identité et d'une somme de contrôle.

Les mêmes notations que précédemment sont utilisées, en particulier φ est l'application linéaire de S_k dans E du code. Notons (f_j) pour j variant de 1 à k + 1 la base canonique de F. L'objectif est de trouver une base (e_i) où i est un entier compris entre 1 et k de E tel que la matrice de φ soit égal à G dans ces bases.

Remarquons tout d'abord qu'aucun vecteur de la base canonique de F n'est élément du code, en effet, le code est de distance minimale égale à deux, et tout vecteur de la base est à une distance de un du mot du code nul.

En revanche, il existe un coefficient c_i tel que f _i + c_i.f _{k + 1} si i est compris entre 1 et k est élément du code. L'espace vectoriel engendré par les vecteurs f _i et f _k+1 est de dimension deux, son intersection avec le code, qui est un hyperplan n'est pas réduite au vecteur nul. Tout vecteur de l'intersection possède une coordonnée non nulle sur f _i car f _k+1 n'est pas élément de l'intersection. Quitte à appliquer une homothétie sur le vecteur, la coordonnée sur f _i peut être choisie égale à un.

Soit e_i l'antécédent du mot du code f_i + c_i.f _{k + 1}. Il suffit alors de démontrer que (e_i) est une base de E et de remarquer que la matrice de φ est bien celle de G dans les bases (e_i) et (f_j) pour conclure.

Considérons une relation de dépendance linéaire de la famille (e_i) :

En appliquant φ à la relation de dépendance linéaire, on obtient :

La relation de dépendance linéaire s'applique sur une base, donc les coefficients sont nuls. La famille (e_i) est libre de cardinal égal à la dimension de E, c'est donc une base de E, ce qui termine la démonstration.

 

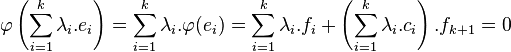
Sommes de contrôle multiple

L'association de plusieurs sommes de contrôle permet d'obtenir un code à même de corriger automatiquement des altérations. Cette logique est utilisée, par exemple, pour le cas du code binaire de Hamming de paramètres [7,4,3]. Trois sommes de contrôles permettent systématiquement de corriger une altération.

Une famille importante de codes correcteur, les code cycliques utilisent les sommes de contrôles dans le contexte de la correction automatique. Si certains cas simples, comme les codes de Hamming utilisent de simples bits de parités, d'autres comme les codes de Reed-Solomon utilisent des tables de multiplication plus complexes issues des extensions de corps finis. La logique est la même, en revanche la somme de contrôle n'est plus équivalente à un ensemble de bits de parité.