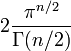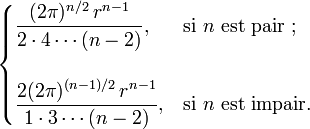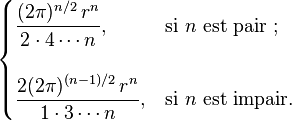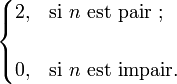Sphère - Définition
La liste des auteurs de cet article est disponible ici.
En contexte topologique
Selon le contexte, en particulier en topologie, le mot sphère (ou n-sphère si on veut rappeler la dimension) peut être utilisé pour désigner n'importe quel espace topologique homéomorphe à une n-sphère au sens défini dans la section précédente.
Généralisation aux autres dimensions
On peut généraliser le concept de sphère à un espace de dimension quelconque dans N. Pour tout entier naturel n, une n-sphere, notée Sn, est l'ensemble des points de l'espace euclidien à (n+1) dimensions qui sont à distance fixée r d'un point de cet espace (r est un réel strictement positif). Par exemple :
- une 0-sphère est la paire des points extrémités de l'intervalle (−r, r) de la ligne réelle,
- une 1-sphère est un cercle de rayon r
- une 2-sphère est une sphère ordinaire
Les sphères de dimension n > 2 sont parfois appelées hypersphères.
L'aire d'une (n−1)-sphère de rayon 1 est
où Γ(z) est la fonction Gamma d'Euler.
Une autre formule pour la surface est
et le volume intérieur est l'aire multipliée par
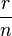
On notera au passage que la caractéristique d'Euler d'une n − sphere vaut