Statistiques élémentaires discrètes - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Algèbre |
| Logique |
| Arithmétique |
| Probabilités |
| Statistiques |
Les statistiques élémentaires discrètes est un domaine des mathématiques élémentaires qui traite le cas où, dans une enquête statistique, le caractère statistique prend un nombre fini raisonnable de valeurs (note, nombre d’enfants, nombre de pièces, secteur d’activité…).
Le caractère statistique étudié est alors appelé caractère discret.
Traitement des données
Les résultats d’une enquête consistent en une liste désordonnée d’informations.
Ex1 - note de la classe X : 10, 9, 12, 11, 10, 8, 14 ,11 ,9 ,16 ,5 ,12 ,10 ,11 ,10 ,13
Ex2 - couleur préférée : bleu, rouge, bleu, bleu, jaune, bleu, rouge, bleu, bleu, jaune, jaune, bleu, jaune.
Il faut alors les trier, par ordre croissant, pour le caractère quantitatif, par genre, pour le caractère qualitatif.
Notes triées : 5, 8, 9, 9, 10, 10, 10, 10, 11, 11, 11, 12, 12, 13, 14, 16
Couleurs préférées triées : bleu, bleu, bleu, bleu, bleu, bleu, bleu, rouge, rouge, jaune, jaune, jaune, jaune.
Cette présentation sous forme de liste est peu exploitable, on décide alors de présenter les résultats de l’enquête sous forme d’un tableau d’effectifs. L’effectif d’une valeur est le nombre de fois où cette valeur apparaît.
Exemple 1: note des élèves
| notes xi | 5 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 16 | Total |
| effectifs ni | 1 | 1 | 2 | 4 | 3 | 2 | 1 | 1 | 1 | 16 |
Exemple 2: couleur préférée
| Couleurs | Effectifs ni |
| Bleu | 7 |
| Rouge | 2 |
| Jaune | 4 |
| Total | 13 |
Lorsque la population étudiée est trop grande, ou bien lorsque l’on cherche à faire la comparaison entre deux populations de tailles différentes, on préfère se ramener à une population de 100, donc travailler en pourcentages, appelés ici fréquences.
Exemple 1: note des élèves
| notes xi | 5 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 16 | Total |
| fréquences fi en % | 6,25 | 6,25 | 12,50 | 25,00 | 18,75 | 12,50 | 6,25 | 6,25 | 6,25 | 100 |
Exemple 2: couleur préférée
| Couleurs | Fréquences fien % |
| Bleu | 53,85 |
| Rouge | 15,38 |
| Jaune | 30,77 |
| Total | 100 |
Présentation des résultats
Les résultats obtenus se présentent, outre le tableau de mesures ci-dessus, par un diagramme en bâtons ou encore par un diagramme en camembert.
Diagramme en bâtons
Reprenons la classe (2) et élevons pour chaque mesure un trait vertical proportionnel au nombre d'élèves. Nous obtenons un diagramme en bâtons.
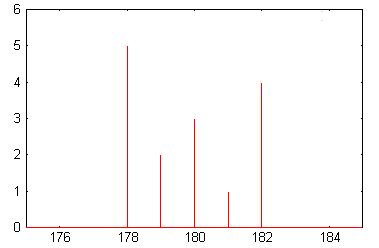
Si nous regroupons maintenant chaque personne ayant une taille comprise entre 179 et 180 cm dans une même classe: la classe des 179 cm -180 cm (c'est ce que nous faisons dans la vie de tous les jours), il est préférable de traiter le caractère comme continu et de tracer un histogramme.
Diagramme circulaire
Pour un caractère qualitatif, on préfère le diagramme circulaire, dit en camembert: on découpe un cercle en « morceaux de tartes » dont la surface est proportionnelle à l'effectif ou la fréquence. Reprenons l'exemple des couleurs et complétons le tableau par le calcul des angles au centre.
| Couleurs | Fréquences fien % | Angle en degré |
| Bleu | 53,85 | 194 |
| Rouge | 15,38 | 55 |
| Jaune | 30,77 | 111 |
| Total | 100 | 360 |
Il ne reste plus qu'à dessiner les « parts de tarte ».