Surface réglée standard - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, et plus précisément en géométrie algébrique, une surface réglée standard est une variété algébrique, qui propose un modèle simple de surface réglée. On obtient ainsi une classification de toutes les surfaces réglées à isomorphisme algébrique près. Fm désigne dans ce langage l'unique surface réglée possédant une courbe géométriquement intègre de self-intersection − m.
Version naïve
Ici, k désigne un corps de caractéristique zéro. On réalise une k-forme de cette surface pour tout m entier, on note Fm le fibré défini de la façon suivante :
On considère deux copies de
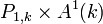
![([x:z],t)\mapsto ([x':z'],t')](https://static.techno-science.net/illustration/Definitions/autres/4/42b93ca9c68430c4d59a5cef82ab3f2d_895f6bf98d5862edf35e0052d40a630e.png)
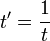
[x:z] désignant un système de coordonnées homogènes de la droite projective P1,k, fibré au-dessus de la droite affine A1(k), dans la première carte.
On note
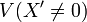
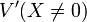
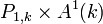
Les deux morphismes
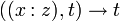
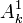
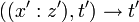
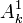
se recollent en un morphisme ρ de Fm sur P1,k qui fait de Fm une surface réglée.
La surface obtenue est appelée surface réglée standard d'indice d'autointersection − m.
Groupes de diviseurs
Pour comprendre cette partie, référez vous à diviseurs ou ici
Quelques courbes tracées sur Fm
On définit d'abord des k-courbes : Co la courbe de trace Z = 0 sur V et Z' = 0 sur V',
Xo la courbe de trace X = 0 sur V et X' = 0 sur V'
Pour tout
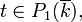
On observe en second lieu qu'il s'agit de courbes géométriquement intègres, dont on peut calculer les intersections.
Intersections des k-courbes
1) les courbes Co,Xo et, pour tout
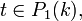
2) De plus Xo.Co = 0,
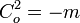
3) Pour tout
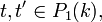
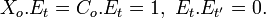
Ces résultat proviennent essentiellement du fait suivant : Le diviseur de la fonction de k(Fm) définie par
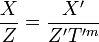
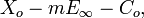
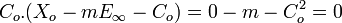
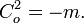
Le groupe de Picard
Définition d'une base des diviseurs
On note f la classe des diviseurs de la fibre
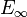
Par commodité, on note h = c0 + mf de sorte que h2 = m ; f2 = 0 ; fh = 1 ;
Une description classique du groupe des diviseurs montre alors que
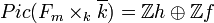
Enfin on calcule sans difficulté la classe canonique K de Fm en explicitant une 2 − forme sur Fm. On obtient K = − 2h + (m − 2)f.
Intérêt de la représentation
Voici une représentation concrète des surfaces réglées standard dans lesquelles le calcul du groupe de Picard s'effectue de façon relativement immédiate.
Pour toutes ces surfaces, il est isomomorphe à
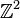
Connaissant la classe des diviseurs (dans le groupe de Picard,) associée à une courbe tracée sur la surface réglée, on peut donc aisément en donner le genre arithmétique d'une courbe.
Un exemple
Si P(T) désigne un polynôme de degré 2m sans facteur multiple, on note P * (T') le polynôme réciproque de P
la courbe R définie par sa trace sur V par l'équation cartésienne
X2 = P(T)Z2 et par l'équation X'2 = P * (T')Z'2 sur la seconde carte
a pour classe de Picard associée : r = 2h et pour genre arithmétique : ga(r) = m − 1
Plus généralement, on peut lire assez facilement sur l'équation cartésienne de la trace d'une courbe dans l'ouvert V, sa classe de Picard, et son genre.

















































