Symétrie (physique) - Définition
La liste des auteurs de cet article est disponible ici.
Symétrie en physique classique
On présente ici les différents contextes de la physique classique où la notion de symétrie est particulièrement importante. On présente la notion d'isotropie, appelée encore symétrie de rotation, ou encore d'homogénéité qui est liée à l'invariance par translation dans l'espace.
Symétrie et conservation
Le théorème de Noether établit que pour toute quantité conservée il existe une symétrie sous-jacente de la théorie.
Aspects mathématiques de la notion de symétrie
Retour sur le théorème de Noether
Point de vue global : groupe de symétrie
Point de vue infinitésimal : algèbre de symétrie
Formalisation générale : groupe et algèbre de Lie
Intégrabilité
L'intégrabilité est la propriété que possèdent certains systèmes d'avoir autant de quantités conservées que de degrés de liberté. Dans ce cas, la donnée de ces constantes du mouvement suffit à déterminer complètement le comportement du système. Le cas le plus simple est celui d'un seul degré de liberté comme un ressort oscillant selon une seule direction ou un pendule oscillant dans un plan. Dans ce cas, si le système est isolé, la seule donnée de l'énergie suffit à connaître toute la dynamique.
Certains systèmes possédant un nombre infini de degrés de liberté possèdent également un nombre infini de quantités conservées. Dans nombre de situations intéressantes cette propriété suffit à déterminer complètement l'ensemble des observables importantes du système. Pour cette raison on dit aussi des modèles qui les décrivent qu'ils sont exactement solubles. En accord avec le théorème de Noether l'algèbre de symétrie de tels systèmes est de dimension infinie.
Exemples de symétries courantes
Symétrie de translation
Appelée aussi invariance sous les translations, cette symétrie dit que les lois physiques (relativité, gravité, électromagnétisme, ...) restent les mêmes en tout point de l'univers.
Symétrie de rotation
Cette symétrie, appelée aussi invariance sous les rotation ou isotropie, désigne la caractéristique topologique d'une théorie ou d'un système physique qui n'est pas transformé par une rotation. L'objet le plus symétrique, sur ce point de vue, est la sphère car, elle reste mathématiquement inchangée par n'importe quelle rotation.
Symétrie en physique quantique
Mécanique quantique
En mécanique quantique, dans laquelle le système est décrit par des états quantiques qui forment un espace mathématique appelé espace de Hilbert, une transformation de symétrie représente le fait de changer ces états quantiques sans pour autant modifier le résultat de la mesure des observables de la théorie.
Le théorème de Wigner montre alors qu'une telle transformation de symétrie doit être représentée par un opérateur possédant certaines propriétés mathématiques précises et agissant sur l'espace de Hilbert.
Si on appelle
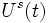
![\left[H(t),U^s(t)\right]+i\frac{\partial U^s(t)}{\partial t}=0](https://static.techno-science.net/illustration/Definitions/autres/c/cf1981230cb71806e5bbc1848faa55be_7a8c5a04affae881bb2d05301ac9ad94.png)
où H(t) est l'opérateur hamiltonien. Dans le cas où l'opérateur de symétrie ne dépend pas explicitement du temps (donc Us(t) = Us) alors cette condition se simplifie en
![\left[H(t),U^s\right]=0](https://static.techno-science.net/illustration/Definitions/autres/f/f0c23911ba208e9cde996efe4b4f12d0_6638219d349ceb6aeec3a6a156d1bc25.png)
Cette relation exprime alors que cette symétrie est associée à une constante du mouvement par rapport au temps.
Dans la représentation de Heisenberg par contre, dans laquelle les états quantiques n'évoluent pas avec le temps, l'opérateur de symétrie prend une autre forme, notée Uh(t) et on peut montrer que la condition d'être une symétrie s'écrit
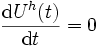
Exemple : le spin
Lorsque le système possède la symétrie
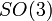
Le théorème de Noether comme point de départ de la théorie quantique des champs
Cas d'une théorie des champs en deux dimensions : la symétrie conforme
La symétrie conforme est la propriété que possèdent certains systèmes de paraître semblables à eux-mêmes en changeant l'échelle d'observation (on dit aussi auto-similaires). En physique statistique on observe une grande classe de tels systèmes au cours d'une transition de phase.
La symétrie conforme peut être réalisée dans des systèmes de dimensions variées mais le cas à deux dimensions est très particulier car le groupe conforme qui est associé à cette symétrie possède alors une dimension infinie. Un aussi grand groupe de symétries impose des contraintes très fortes sur la structure des observables du système et dans nombre de situations la symétrie conforme est suffisante pour connaître exactement toutes les caractéristiques physiques du système.
Les contraintes supplémentaires apportées par la symétrie conforme peut amener des systèmes en apparence différents d'un point de vue microscopique à partager des propriétés macroscopiques communes lors de transitions de phase, on appelle cette propriété universalité.

















































