Théorème d'unicité de Stokes - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le théorème d'unicité de Stokes, dû à George Stokes, trouve des applications en mécanique des fluides.
Énoncé et démonstration
Ce théorème peut s'énoncer de la manière suivante : étant donnée une surface équipotentielle Σ qui renferme en son intérieur toute la matière, le potentiel extérieur à Σ n'est pas modifié lorsqu'on modifie la répartition des masses de telle façon que Σ reste la même surface équipotentielle. En termes plus mathématiques, ce théorème peut aussi s'énoncer comme suit :
Théorème d'unicité de Stokes — Une fonction V harmonique à l'extérieur d'une équipotentielle Σ est déterminée de façon unique par ses valeurs sur Σ.
La démonstration de cette proposition est aisée. En effet, soit un champ de densité qui donne lieu à un potentiel V, et soit Σ une surface fermée régulière (de normale extérieure unitaire
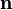
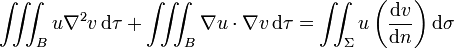
On trouve alors
![\iiint_B \left[V^{*} \nabla^2 V^* + (\nabla V^*)^2\right]\,\mathrm d \tau = \iint_{\Sigma} V^* \left(\frac{\mathrm d V^*}{\mathrm d n}\right) \mathrm d \sigma](https://static.techno-science.net/illustration/Definitions/autres/d/db33978712425f6904ae88b09cc61d93_fbef4f571dea1042f1892ab5bf20ed36.png)
Désignons par CB le complémentaire du volume B intérieur à la surface Σ, autrement dit la région extérieure à Σ. V * étant la différence de deux fonctions harmoniques dans CB est elle-même une fonction harmonique dans CB :
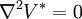
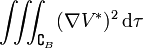
ou encore
![\iiint_{\complement_B} \left[ \left( \frac{\partial V^*}{\partial x_1} \right) ^{2} + \left( \frac{\partial V^*}{\partial x_2} \right)^2 + \left( \frac{\partial V^*}{\partial x_3} \right)^2 \right] \mathrm{d} x_1 \mathrm{d} x_2 \mathrm{d} x_3 = 0](https://static.techno-science.net/illustration/Definitions/autres/7/7dcca02bc79f09dd5b5cdd80a0fff2f9_9daa4773e47b3d2197a769ecc767493c.png)
Cette relation implique nécessairement que
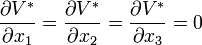
ou encore
Or, V * étant une fonction harmonique, on doit avoir
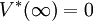
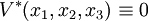
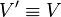
Principe de Dirichlet
D'un point de vue plus mathématique, signalons encore que le théorème de Stokes montre qu'il ne peut y avoir qu'une seule fonction harmonique V qui prend des valeurs données sur une surface-frontière Σ. Il n'établit pas l'existence d'une telle fonction harmonique. L'assertion que pour des valeurs-limites arbitrairement prescrites il existe toujours une fonction harmonique V qui prend sur Σ les valeurs-limites données s'appelle le principe de Dirichlet.
Nous sommes en présence de deux cas distincts : V est harmonique à l'extérieur de Σ et V est harmonique à l'intérieur de Σ. Le principe de Dirichlet a été prouvé dans des situations très générales par des travaux de nombreux mathématiciens, parmi lesquels il convient de mentionner Henri Poincaré et David Hilbert ; la démonstration en est fort difficile. Le problème qui consiste à calculer la fonction harmonique (à l'intérieur ou à l'extérieur de Σ) à partir de ses valeurs-limites sur Σ est le problème de Dirichlet, ou encore le premier problème aux valeurs-limites de la théorie du potentiel. Ce problème se pose notamment en géodésie.