Théorème de Minkowski - Définition

Interprétation géométrique

Exemple de réseau dans R³.

Exemple de convexe traité par le théorème de Minkowski.

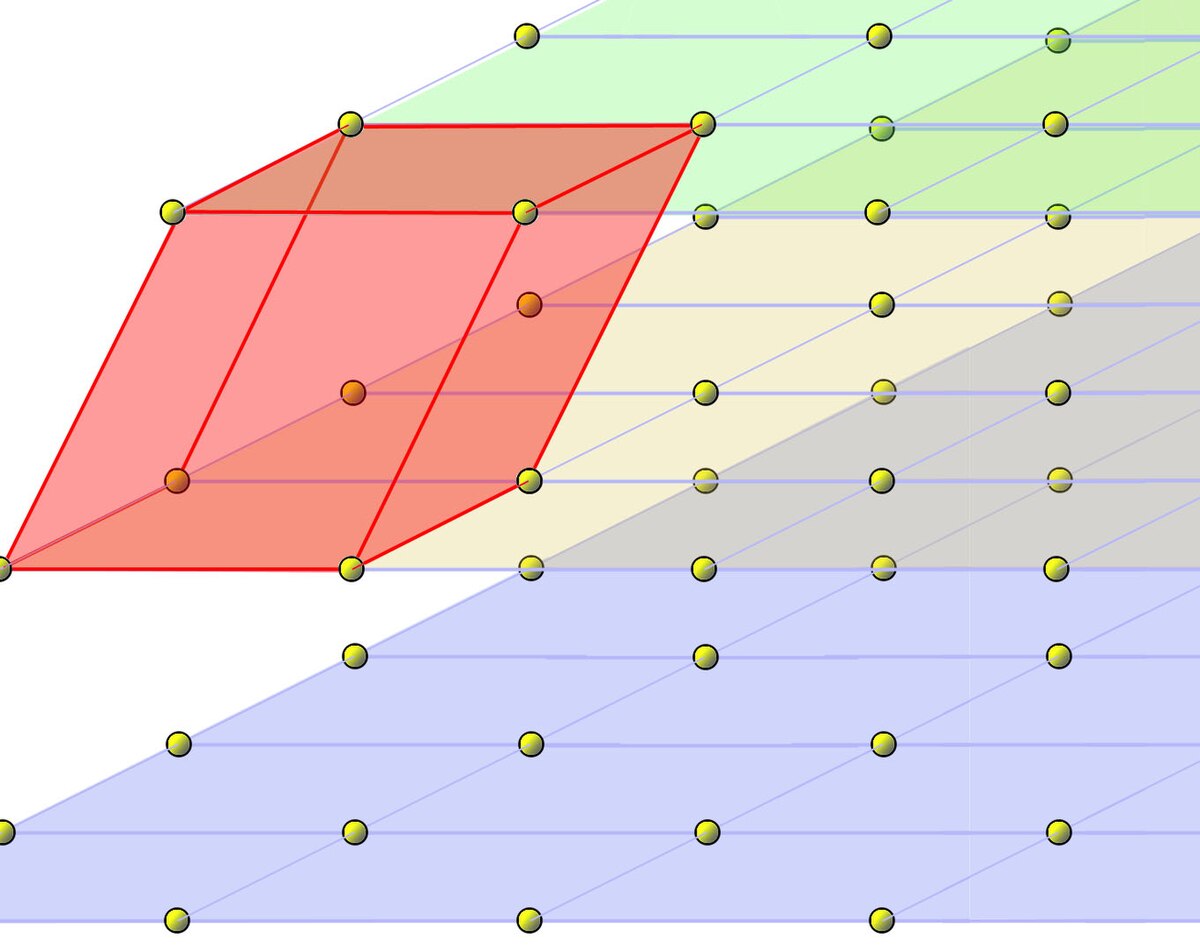
Un réseau est un groupe groupe additif de R^d discret, Une telle structure est nécessairement un Z module admettant une base B. Pour s'en convaincre il suffit d'étudier les propriétés d'un groupe abélien de type fini. Un Z module est un quasi espace vectoriel. Les scalaires sont munis d'une structure d'anneau et non de corps. Par définition d'un réseau, la base est de cardinal d et est aussi une base de R^d en tant qu'espace vectoriel sur R. Le réseau est composé des points dont les coordonnées dans la base B sont entières. On obtient un maillage régulier de l'espace, à l'image de la figure de gauche. Les points du réseau sont représentés par les petites billes. Un exemple de réseau est formé des points à coordonnées entières dans la base canonique de R^d. Le premier énoncé est ainsi un cas particulier du deuxième.

Un domaine fondamental est constitué des points dont les coordonnées dans la base B sont dans l'intervalle [0, 1[, le volume fondamental est le volume du domaine fondamental. Dans l'exemple précédent, il est égal à 1. Il est illustré sur la figure de gauche en rouge. Un domaine fondamental est toujours un parallélépipède.

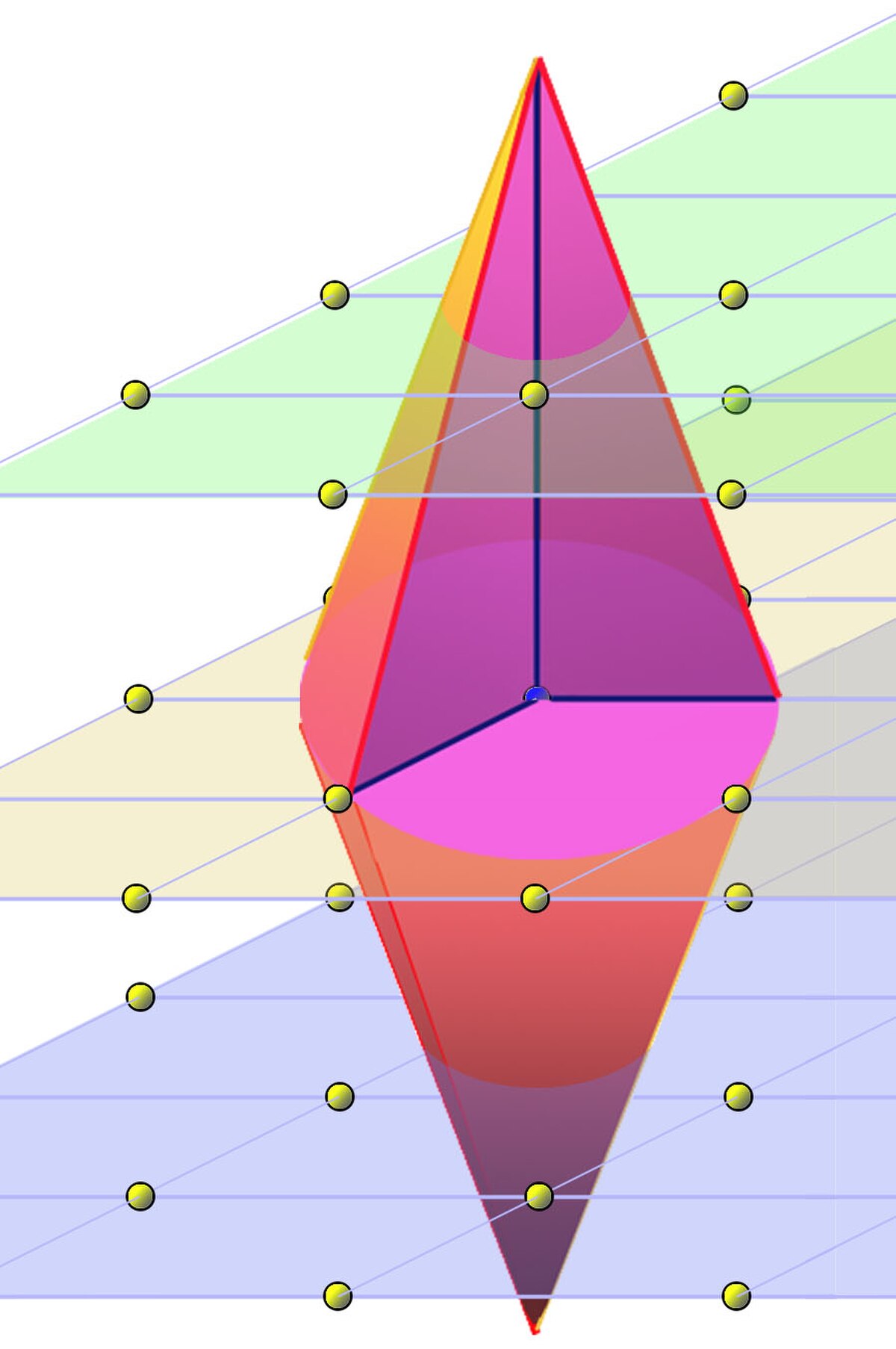
Dire que le convexe C est symétrique par rapport à l'origine signifie que si le vecteur α est élément du convexe, alors -α est aussi élément du convexe. La figure de droite représente un tel ensemble, si le point bleu représente l'origine. Il ne contient aucun autre point du réseau que l'origine, le théorème affirme que son volume est inférieur à 2³ soit 8 fois le volume fondamental. En effet, dans l'exemple d est égal à 3, .

La forme du convexe donné en exemple n'est pas le fruit du hasard, on la trouve en théorie algébrique des nombres. Elle correspond à une boule pour une métrique choisie dans le cas d'un anneau d'entiers algébriques de degré 3 ayant un plongement réel et deux imaginaires (cf groupe des classes d'idéaux). Une démonstration clé utilise le théorème un théorème connexe sur un convexe de cette forme.

Applications

Ce théorème est habituellement utilisé pour démontrer deux résultats importants en théorie algébrique des nombres : le théorème des unités de Dirichlet, et la finitude du groupe des classes.

Une autre application élégante est la démonstration du théorème des quatre carrés de Lagrange.