Théorème du redressement - Définition

Explications

Vocabulaire

Quelques symboles et termes nécessitent une explication. Le premier énoncé utilise le signe * dans une composition d'une fonction f et d'un champ de vecteurs X. Ici f est une application de V dans un ouvert inclus dans Ω. L'application qui à x associe X(f(x)) est bien définie sur X. Comme l'application f est un difféomorphisme, elle admet une différentielle au point x et cette différentielle est inversible. Ce qui assure que la définition suivante est bien cohérente :

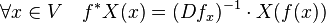
Pour éviter une débauche de parenthèses, ici l'image d'un vecteur v par une application linéaire a est notée a.v.

L'équation différentielle x' = X(x) admet toujours une unique solution s vérifiant s(0) = p. La fonction qui à (t, p) associe α(t, p) définie comme la valeur de l'équation différentielle vérifiant la condition de Cauchy précédente est une fonction continue appelée flot. Si X est de classe C^k, alors le flot est aussi de classe C^k.

Un hyperplan H_a affine, de direction H contenant p₀ est dit transverse à X en p₀ si la somme directe de H et de R.X(p₀) est égal à E. Une section transverse à X est un ouvert S de H tel que l'hyperplan H_a soit transverse à X en tout point p de S. Si H_a est transverse à X en p₀, une section transverse contenant p₀ existe toujours. En effet, la composée de la projection sur R.X(p₀) parallèlement à H du champ X est non nulle en p₀ et est continue. Il existe un ouvert de p₀ sur lequel cette projection est supérieur à un nombre réel strictement positif. L'intersection de ce voisinage et de H_a, est une section transverse à X contenant p₀.

Interprétation

Une boîte à flot permet de contrôler le flux au voisinage d'un point p₀.

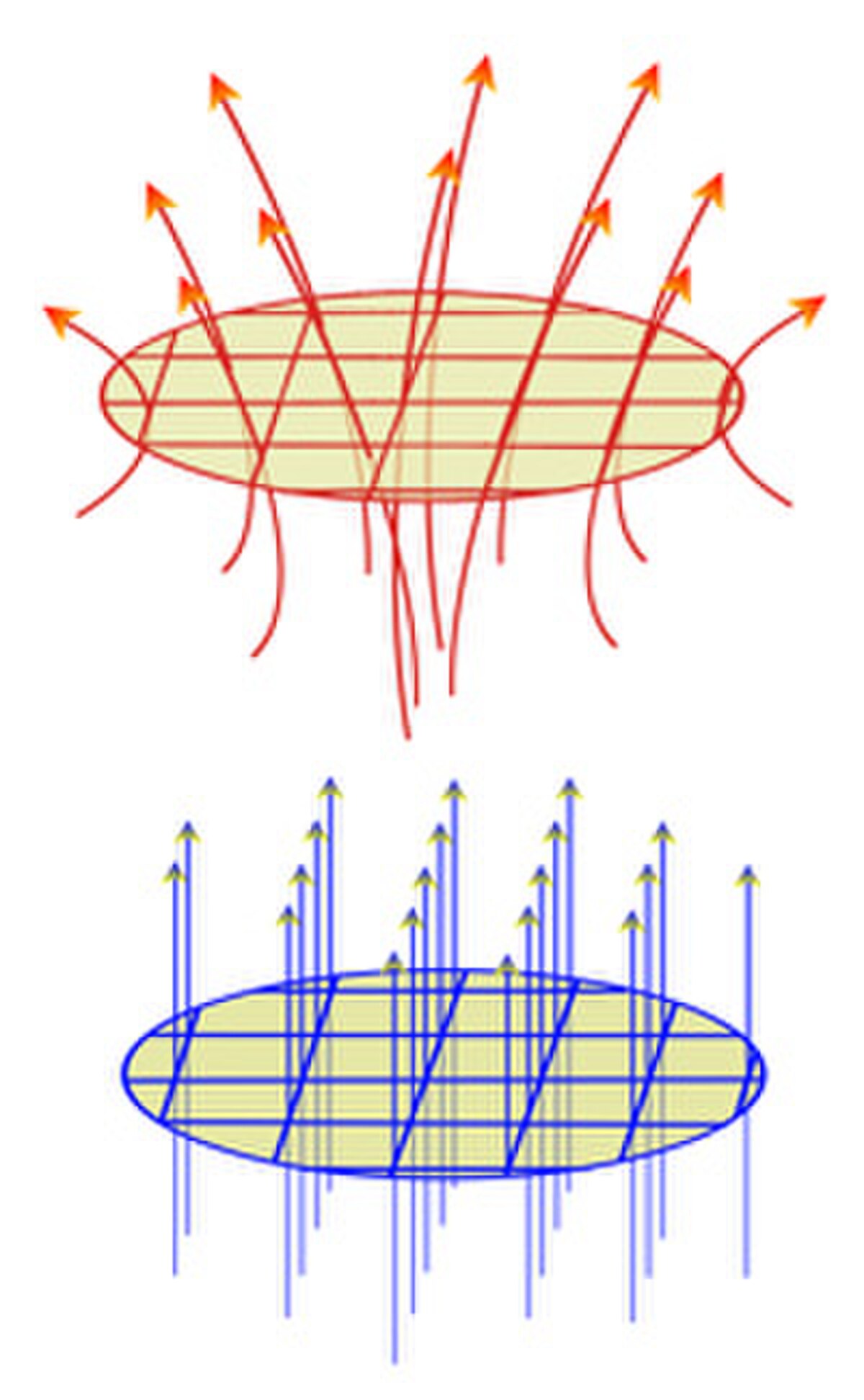
Ce théorème indique que localement et à un difféomorphisme près, on peut toujours considérer un champ de vecteurs comme constant. Le théorème redresse le champ à l'image de la figure de gauche. Un champ de classe C¹ est à l'image de la figure rouge et jaune, il est possible de lui appliquer un difféomorphisme à travers la loi de composition * qui lui donne l'apparence du champ bleu et jaune au dessous.

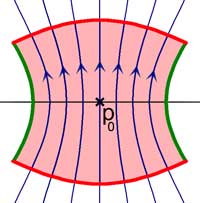
Une autre forme indique la possibilité de construire une boîte à flot. Dans le monde redressé, la boîte à flot ressemble à une boîte de conserve contenant en son milieu le point p₀. La base circulaire correspond à la section et le flot traverse la boite de sa base à son sommet à travers les trajectoires rectilignes uniformes et verticales. Ainsi, le flot ne rentre que par la base et ne sort que par le sommet, la paroi verticale est parallèle au flot et n'est pas traversée par lui. Dans le monde original, la boîte à flot est déformée par le difféomorphisme, mais garde cette propriété, la base reçoit le flot entrant, le sommet le flot sortant et la paroi reste parallèle au flot, à l'image de la figure de droite. Une telle boîte permet un contrôle du flux au voisinage de p₀.

Un exemple d'usage d'une boîte à flot est la démonstration du théorème de Poincaré-Bendixson. Une telle boîte permet le contrôle de la trajectoire aux alentours d'un point bien choisi. A l'aide du théorème de Jordan, elle permet d'établir l'impossibilité d'une configuration chaotique si E est un plan, si l'équation différentielle est autonome dans une zone compacte de Ω invariante par le flot.