Théorie de la réponse linéaire - Définition

Réponse linéaire et relations de réciprocité d'Onsager

La théorie de la réponse linéaire permet de donner une justification microscopique des relations de réciprocité d'Onsager. On obtient en fait une égalité plus générale:

Imχ_lk(ω) = Imχ_kl(ω)

dans le cas où les opérateurs A_l et A_k sont tous les deux invariants par renversement du temps et où le système n'est pas placé dans un champ magnétique. Lorsque le système est placé dans un champ il faut changer le signe du champ magnétique dans le membre de droite de l'égalité. Si les opérateurs A_l ou A_k changent de signe sous le renversement du sens du temps (par exemple si ce sont deux courants), il faut appliquer le même nombre de changements de signe au membre de droite que d'opérateurs non invariants par renversement du sens du temps (dans le cas de deux courants, on doit appliquer deux changements de signe, donc le signe final ne change pas dans le membre de droite).

Perturbations non mécaniques

Dans ce qui précède, on a admis que la fonction de réponse pouvait être obtenue en calculant l'évolution d'un système dont le Hamiltonien dépend explicitement du temps par la théorie de perturbations. Dans ce cas, on parle de perturbations mécaniques.

Cependant, si on veut pouvoir définir des quantités comme la conductivité thermique ou la constante de diffusion, ce cadre est trop restrictif. En effet, un gradient thermique ne peut pas être vu comme une force agissant sur les particules d'un système. On parle alors de perturbations non mécaniques.

Dans le cas du transport thermique, une généralisation de la formule de Kubo a été proposée par J. M. Luttinger en 1964. Cette généralisation est basée sur une hypothèse d'équilibre local.

Règles de somme

Les règles de somme sont des identités satisfaites par les fonctions de réponse de la forme:

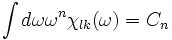
Où C_n est la valeur moyenne d'un certain opérateur dans l'état d'équilibre. Ces règles de somme sont obtenues en intégrant par partie la formule de transformation de Laplace. L'intégration par partie fait apparaître des dérivées de l'opérateur A_l qui peuvent être représentées à l'aide de l'équation du mouvement de Heisenberg. On obtient ainsi: .

Relations de Kramers-Kronig

Le fait que la fonction de corrélation s'annule pour les intervalles de temps négatif est une conséquence de la causalité. En effet, cela signifie qu'au temps t, la réponse du système ne dépend que des valeurs de la perturbation aux temps t' < t. Cette annulation de la fonction de corrélations au temps négatif implique que sa transformée de Laplace est holomorphe dans le demi-plan supérieur. On peut donc utiliser le théorème de Cauchy pour obtenir une expression de la fonction de réponse pour Im(z) > 0 en fonction de sa valeur sur l'axe réel. On obtient:

En faisant et en utilisant les identités sur les distributions, on obtient les relations de Kramers-Kronig:

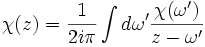
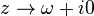
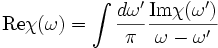
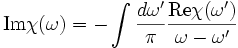
Formalisme de Mori-Zwanzig

Le formalisme de Mori-Zwanzig utilise des opérateurs de projection pour obtenir des expressions des fonctions de réponse inverse. Par exemple, le formalisme de Mori-Zwanzig permet d'obtenir une expression pour la résistivité plutôt que la conductivité.