Théorie de la réponse linéaire - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En physique statistique hors d'équilibre, la théorie de la réponse linéaire permet de définir les susceptibilités et les coefficients de transport d'un système au voisinage de l'équilibre thermique indépendamment des détails du modèle. La théorie de la réponse linéaire a été développée dans les années 1950 par Greene, H. B. Callen, Ryogo Kubo.
Formalisme général
Le Hamiltonien du système
Dans la théorie de la réponse linéaire, on suppose que le système considéré est décrit par un certain Hamiltonien d'équilibre H0, perturbé par un Hamiltonien perturbatif dépendant du temps H1(t), qu'on peut expliciter sous la forme:
| H1(t) = | ∑ | λi(t)Ai |
| i |
ou les λi(t) sont les facteurs perturbatifs et les opérateurs hermitiens Ai sont des observables du système, de sorte que le Hamiltonien total du système est:
| H = H0 + H1(t) = H0 + | ∑ | λi(t)Ai |
| l |
Il en ressort que le formalisme naturel d'un système en réponse linéaire est la représentation d'interaction.
Explicitation de la matrice densité
La matrice densité est affectée par la perturbation du hamiltonien. Pour la matrice densité, l'équation de Schrödinger s'écrit:
|
|
Attention! Ceci n'est pas une équation de Heisenberg et la matrice densité ρ(t) n'est pas un opérateur! (Voir le signe du commutateur pour s'en convaincre!) Si nous baptisons ρ0 la matrice densité du système non perturbé(c’est-à-dire du système à l'équilibre thermique), ρ(t) la matrice densité du système perturbé(c’est-à-dire du système hors équilibre), δρ(t) l'écart de la matrice densité du système perturbé calculé au premier ordre de perturbation, l'équation de la matrice densité se réduit à:
![i\hbar \partial_t\delta\rho(t)= [H_1(t),\rho_0]+ [H_0,\delta\rho(t)]](https://static.techno-science.net/illustration/Definitions/autres/0/06f7611027ea8a2acb1073a530e5094b_c0b597f495006a5a289e76453d8748fb.png)
d'où la solution:
![\delta\rho(t)= {1\over{i\hbar}}\int_{-\infin}^t e^{-i(t-\tau)H_0/\hbar}[H_1(\tau),\rho_0]e^{i(t-\tau)H_0/\hbar} d\tau](https://static.techno-science.net/illustration/Definitions/autres/f/fe7d825b215e590f4fbb15d6716710de_493b0de4fb3b3c653201d8bf4854d75f.png)
ce qui permet d'acceder à ρ(t)
calcul des observables et des fonctions de réponse
En calculant au premier ordre de la théorie des perturbations on obtient la matrice densité ρ(t) du système. Cette matrice peut être utilisée pour extraire les moyennes thermiques et quantiques des observables:
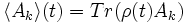
En dernier ressort, en introduisant la fonction de réponse retardée χkl(t) les observables du système sont données par:
|
|
Où on identifie la fonction de réponse χkl(t) par:
|
|
où θ est la fonction de Heaviside (qui traduit ici le principe de causalité),
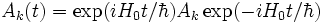
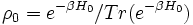
La définition de la fonction de réponse est due à Ryogo Kubo (1956).
Comme la fonction de réponse χkl(t) s'annule pour t < 0 (à cause du principe de causalité), on peut définir sa transformée de Laplace imaginaire (nommée encore Fourier unilatérale), qui est égale dans ce cas précis à sa transformée de Fourier simple:
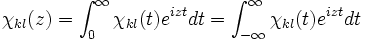
qui est donc une fonction holomorphe pour Im(z) > 0 d'après les propriétés de la transformation de Laplace.
Première application: résistivité électrique
L'intérêt de la théorie de la réponse linéaire vient de ce qu'aucune hypothèse n'est nécessaire sur le Hamiltonien H0 pour définir la fonction de réponse. Cela permet par exemple de définir la conductivité en considérant:
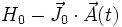
où
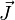
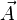
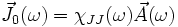
En tenant compte des équations de Maxwell, cette équation permet de montrer que la conductivité est:
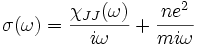
Le second terme est une contribution diamagnétique qui vient de ce que le courant est
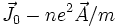
Le calcul de la conductivité est donc réduit au calcul de la fonction de réponse χJJ. Ce calcul peut être effectué soit par des méthodes numériques comme la méthode Monte-Carlo quantique, ou la méthode de Lanczos ou bien par des méthodes analytiques comme la sommation de diagrammes de Feynman.
Autre application: relaxation magnétique
De la même façon, on peut définir avec la théorie de la réponse linéaire d'autres grandeurs physiques comme la constante diélectrique ou la susceptibilité magnétique. La susceptibilité magnétique est en particulier utile dans l'étude de la résonance paramagnétique électronique.
Dans le cadre de la théorie de la réponse linéaire, il est aussi possible d'étudier les processus de relaxation en calculant la réponse à une perturbation de la forme:
λ(t) = λ0exp(εt)θ( − t)
et en prenant la limite
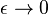
Ainsi, la théorie de la réponse linéaire permet de définir le temps de relaxation 1 / T1 résultant du couplage hyperfin entre les spins nucléaires et les spins électroniques sans faire d'hypothèse a priori sur le modèle qui décrit les spins électroniques.
Enfin, la théorie de la réponse linéaire permet grâce au théorème de fluctuation-dissipation de définir les fonctions de réponse en termes des fonctions de corrélation symétriques:
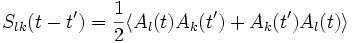
![i\hbar \partial_t\rho(t)= [H(t),\rho(t)]](https://static.techno-science.net/illustration/Definitions/autres/2/24f35469c224d377bb6d7f99deec5878_aa101c760f92770ce057cdb5dd31a5f7.png)
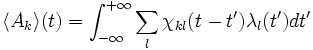
![\chi_{kl}(t-t')=\frac{i}{\hbar} \theta(t-t') \langle [A_k(t),A_l(t')]\rangle](https://static.techno-science.net/illustration/Definitions/autres/9/916254841bf5173decfe37fa9a123d37_6f6ae45b6a2576954781bb32bdfdc5f9.png)

















































