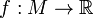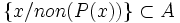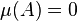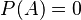Ensemble négligeable - Définition

En théorie de la mesure, un ensemble négligeable ou un ensemble de mesure nulle est une partie d'un ensemble mesuré dont la définition dépend de la mesure que l'on utilise ou plutot de sa classe d'équivalence. À un niveau élémentaire, il est possible d'aborder la notion d'ensemble négligeable pour un certain nombre d'espaces (dont la droite réelle) sans avoir à introduire une mesure. Historiquement, la notion d'ensemble négligeable est antérieure.

• Une partie mesurable d'un ensemble mesurable , mesuré avec la mesure , est dite de mesure nulle lorsque .
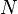
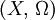
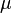
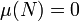
• Une partie N de X est dite négligeable lorsqu'elle est incluse dans une partie de mesure nulle.

L'ensemble des parties négligeables d'un ensemble mesuré (X,μ) a les propriétés suivantes :

• Tout sous-ensemble mesurable d'une partie négligeable a une mesure nulle, conséquence de la monotomie des mesures.
• Tout sous-ensemble d'une partie négligeable est négligeable.
• Toute union dénombrable d'ensembles (mesurables) de mesure nulle est mesurable et de mesure nulle, conséquence de la sous-additivité des mesures.
• Toute union dénombrable d'ensembles négligeables est négligeable.

A priori, la définition de partie négligeable parait plus forte, car autorise des ensembles non mesurables. Toutefois, il est loisible de compléter la tribu Ω en une tribu Ω' incluant les ensembles négligeables non mesurables, et sur laquelle se prolonge la mesure μ. Il est à remarquer que cette complétion dépend de la définition d'ensembles négligeables. On parle alors de mesure complète ; pour une mesure complète, tout ensemble négligeable est mesurable et donc de mesure nulle.

Éléments historiques

Ensembles négligeables pour la mesure de Lebesgue

Exemples

Dans les espaces , la mesure généralement utilisée est la mesure de Lebesgue, unique mesure à proportionnalité près invariante par les isométries. Pour cette mesure, tout singleton a une mesure nulle. Donc, en utilisant la deuxième propriété énoncée ci-dessus, on voit sans difficulté que tout sous-ensemble dénombrable de est négligeable.

Ainsi, si on note la mesure de Lebesgue sur alors .

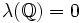
Nature des ensembles de mesure de Lebesgue nulle

Contrairement à ce que l'on pourrait croire intuitivement, les parties de qui sont de mesure de Lebesgue nulle ne sont pas forcément dénombrables. En effet, l'exemple le plus classique est la réalisation triadique de l'ensemble de Cantor : cet ensemble est un borélien de mesure de Lebesgue nulle mais il n'est pas dénombrable (car il est équipotent à ). Un autre ensemble remarquable de mesure nulle est l'ensemble de Besicovitch : il contient une droite dans toutes les directions. Il peut être construit de plusieurs façons, notamment comme dual de l'ensemble de Cantor "quatre coins".

Presque tout

Une propriété est dite vérifiée par presque tout un ensemble ou presque tous les éléments d'un ensmble si elle est vérifiée par un ensemble vérifiant une des propriétés suivantes:

En théorie des ensembles

Si Y est le sous-ensemble de points x d'un ensemble infini X ne vérifient pas un prédicat P(x), alors on dit que P est vérifiée pour presque tous les éléments de X si le cardinal de Y est strictement inférieur au cardinal de X.

• Presque tous les nombres réels sont des irrationnels. En effet, il existe une infinité dénombrable de nombres rationnels et une infinité ayant la puissance du continu de nombres réels (voir argument de la diagonale de Cantor).

Une partie A de est dite asymptotiquement dense si :

.

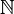
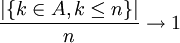
• Presque tous les entiers sont non premiers. En effet, le densité de nombres premiers inférieurs à un entier n est équivalente à 1/ln(n) quand n tend vers l'infini.

Le concept de " presque partout "

Définition

Ce concept d'ensemble négligeable permet notamment de définir le concept de " presque partout ". En effet, si est une mesure sur un espace mesurable , une proposition dépendant d'une variable est dite vraie μ(dx)-presque partout s'il existe un ensemble mesurable A appartenant à tel que :

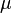
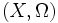
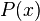
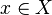
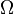
Une propriété est dite vraie presque partout si l'ensemble des points où elle est fausse est de mesure nulle. Ainsi, une fonction sera égale à une fonction μ-presque partout si l'ensemble .

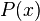
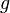
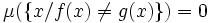
Dans un ensemble ayant la puissance du continu, un ensemble dénombrable est de mesure nulle. C'est ce résultat qui permet d'affirmer que la fonction qui à un réel lui associe 1 si le réel est rationnel, 0 s'il est irrationnel, est nulle presque partout.

L'ensemble de Cantor est un exemple de sous-semble indénombrable de [0,1] mais de mesure nulle. Presque tous les réels entre 0 et 1 sont hors de l'ensemble de Cantor.

Exemple

• Si est une fonction d'un espace mesuré à valeurs positives telle que est intégrable au sens de Lebesgue , alors :

si et seulement si µ-presque partout.

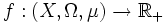
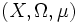
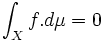
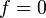
" Presque sûrement "

En probabilités, on préfère en général parler d'une propriété vraie presque sûrement, au lieu d'utiliser l'expression " presque partout ". Une propriété est vraie presque sûrement lorsqu'elle est vérifiée dans un ensemble dont la probabilité est égale à 1. La probabilité étant une mesure et l'espace mesurable ayant une probabilité de 1, c'est bien un cas particulier de la situation précédente.

Dans l'espace probabilisé (ensemble Ω, d'une tribu sur Ω et mesure P sur cette σ-algèbre telle que P(Ω) = 1), la propriété R est vraie presque sûrement s'il existe un ensemble mesurable A appartenant à tel que :

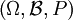
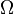
Ce qui est équivalent à dire que P(Ω\A)=1, par propriété des probabilités.

La notion de propriété vérifiée presque sûrement entraîne celle de convergence presque sûre en convergence de variables aléatoires.

converge presque sûrement vers ssi . La convergence presque sûre implique les autres propriétés de convergences usuelles en théorie des probabilités (convergence en probabilités et convergence en loi). En ce sens, elle est la plus "forte" des lois de convergence.

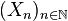
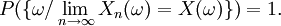
L'expression presque tout intervient couramment dans différents domaines des mathématiques. Il peut avoir un sens probabiliste, topologique ou ensembliste. En général, le contexte précise le sens de l'expression.

En topologie

Dans un espace de Baire, presque tous les points vérifient une propriété lorsque l'ensemble des points la vérifiant contient l'intersection dénombrable d'ouverts denses. Par le théorème de Baire, cette intersection est non vide et dense.

• Presque tous les réels sont des irrationnels.
• Presque toutes les fonctions continues sont non dérivables.
• Presque tous les points de sont des valeurs régulières d'une fonction différentiable où M est un segment de où n'importe quelle variété compacte.