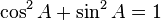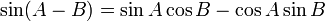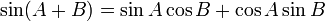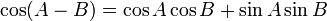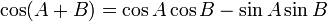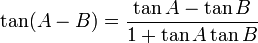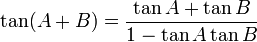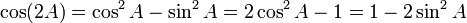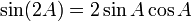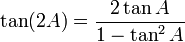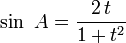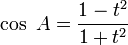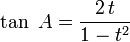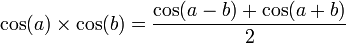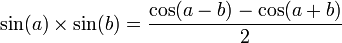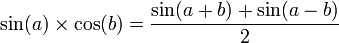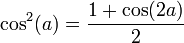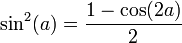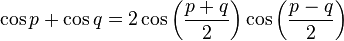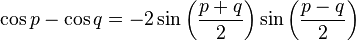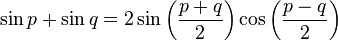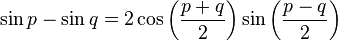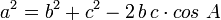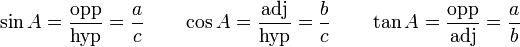Trigonométrie - Définition

Formules de trigonométrie

Identité fondamentale

Quel que soit l'angle A, on a (d'après le théorème de Pythagore):

Formules d'addition et de différence

Formules de l'arc moitié

Ces formules sont importantes à retenir car elles interviennent dans de très nombreux problèmes. En posant : , on a alors :

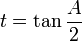
Formules de développement et de factorisation (Formules de Simpson)

Développement

Factorisation

Théorème d'Al-Kashi ou Loi des cosinus

Cette formule a une importance particulière en triangulation et a servi à l'origine en astronomie (voir Théorème d'Al-Kashi pour plus de détails). On doit au mathématicien Ghiyath al-Kashi, de l'école de Samarcande, de mettre le théorème sous une forme utilisable pour la triangulation au cours du XV^e siècle.

Résoudre un triangle

C'est, étant donné un côté et deux angles adjacents, ou un angle et deux côtés adjacents, ou à la rigueur deux côtés b et c et l'angle B, trouver le triangle correspondant, c'est-à-dire, a, b, c, A, B, C (et vérifier une des règles non appliquée dans le processus). On résout ce genre de problème à l'aide des formules précédentes (plus la formule de projection évidente a = b.cosC +c.cosB).

Exemple : Sur l'axe Ox, OB = 1 et OC = 1.5 . OBM = 60° et OCM = 30° Trouver M  :

On résout ainsi : faire l'épure ; M se trouve en (x= 0.75 ; y = 0.45) environ . Raisonner : triangle BMC : B = 120°, C = 30° donc M = 30° ; donc triangle isocèle en B : BM = 0.5 ; puis CM = 2.(0.5).cos C = sqrt(3)/2. Soit H la projection de M sur l'axe : HM = y et angle HMB = 30°. Il en résulte que y = sqrt(3)/4 = 0,433 et x = 1-(0,5)/2 = 0,75 . La distance OM = sqrt(3)/2 = MC, et azimut de M = 30°, angle OMB = 90°.

Il est rare du point de vue cadastral que les cas soient aussi simples.

En général on demande 4 à 6 ChS (chiffres significatifs) : les calculettes ont considérablement réduit le travail assez fastidieux de "réduction des triangles". Rappelons que la mesure du degré du méridien terrestre de Paris s'est effectué de la sorte entre Malvoisine et Montlhéry par l'abbé Picard, dans le milieu du XVII^e siècle.

La surface S du triangle se calcule par la formule des sinus ou la formule d'Héron (d'Alexandrie) qui s'en déduit : S² = p(p − a)(p − b)(p − c).

Article détaillé : Résolution d'un triangle

Trigonométrie

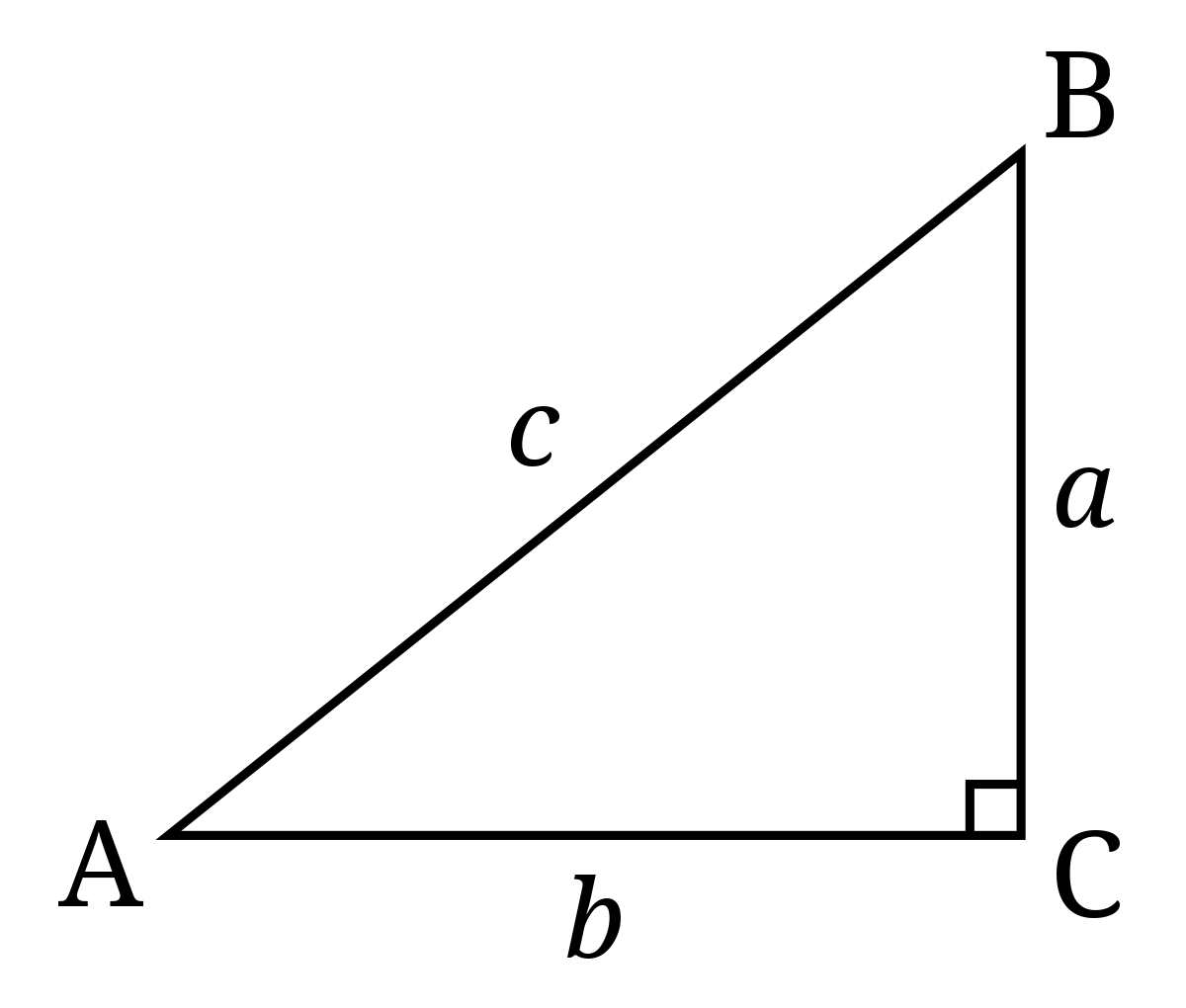
Une définition possible des fonctions trigonométriques est d'utiliser les triangles rectangles, c’est-à-dire les triangles qui possèdent un angle droit (90° (degrés) ou π/2 radians).

Et parce que la somme des angles d'un triangle fait 180° (ou π radians), l'angle le plus grand dans un tel triangle est l'angle droit. Le côté le plus long dans un triangle rectangle, c’est-à-dire le côté opposé à l'angle le plus grand (l'angle droit), s'appelle l'hypoténuse.

Dans la figure à droite, l'angle forme l'angle droit. Le côté AB l'hypoténuse.

Les fonctions trigonométriques se définissent ainsi, avec l'angle  :

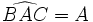
Avec opp pour côté opposé, adj pour côté adjacent et hyp pour hypoténuse.

Ce sont les fonctions trigonométriques les plus importantes et il en existe beaucoup d'autres. Elles ont été définies pour les angles entre 0° et 90° (soit entre 0 et π/2 radians). En utilisant le cercle unité, on peut étendre cette définition.