Entropie des trous noirs - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
L'entropie des trous noirs est une notion issue de l'étude des trous noirs dans le cadre de la relativité générale et de la théorie quantique des champs, en relation avec la thermodynamique. Depuis les années 1970, il a été montré par les physiciens Stephen Hawking et Jacob Bekenstein que les trous noirs possédaient, tout comme les objets ordinaires une entropie, c'est-à-dire une mesure de la quantité d'information qu'ils renferment.
Contexte historique
Le concept d'entropie des trous noirs est né suite à un article de Stephen Hawking qui s'interrogeait sur des aspects énergétiques liés à la collision de deux trous noirs. Si l'on considère deux trous noir de masses M et M', on peut associer une énergie à ce système qui vaut, d'après la célèbre formule E=mc2, (M + M')c2, où c est la vitesse de la lumière. Si l'on imagine que ces deux trous noirs entrent en collision, le produit de la collision sera un trou noir. La conservation de l'énergie implique que l'énergie totale du système soit la même que précédemment, cependant, lors de leur collision, les deux trous noirs vont vraisemblablement rayonner une quantité non négligeable d'énergie sous forme d'ondes gravitationnelles. L'étude de Hawking avait pour but de déterminer quel « rendement » optimal l'on pouvait tirer d'un tel événement, c'est-à-dire quelle quantité maximale d'énergie pouvait être extraite des deux trous noirs sous forme d'ondes gravitationnelles. Le résultat trouvé par Hawking fut surprenant et très général : quelles que soient les masses, les charges électriques et les moment cinétiques des deux trous noirs, la quantité maximale d'énergie qu'ils pouvaient rayonner était telle que la surface du trou noir final devait être supérieure où égale à la somme des deux surfaces des trous noirs. Un tel résultat présentait une analogie frappante avec le second principe de la thermodynamique, qui stipule que l'entropie d'un système ne peut que croître au cours du temps. Il était donc tentant d'associer à un trou noir une entropie proportionnelle à sa surface, mais la thermodynamique indique qu'un système physique auquel on associe une entropie doit également posséder une certaine température. De plus, un objet porté à une température non nulle émet un certain rayonnement électromagnétique. À l'inverse, un trou noir est un objet qui par définition n'émet aucune forme de matière ou de rayonnement. Il semblait donc y avoir impossibilité de pouvoir associer de quelque manière que ce soit une entropie aux trous noirs.
Peu après, le physicien Jacob Bekenstein étudia la variation des paramètres décrivant un trou noir lors de l'absorption par celui-ci d'une particule élémentaire. Il montra que si l'on suppose la particule strictement ponctuelle, alors pour certaines trajectoires de celle-ci, la surface du trou noir pouvait rester constante. Cependant dès que l'on tenait compte du fait que toute particule élémentaire se voit assigner une certaine extension spatiale par la mécanique quantique (voir longueur d'onde de Compton), alors la surface d'un trou noir augmentait nécessairement lors de l'absorption de la particule, et ce d'une quantité proportionnelle à une fraction de la surface de Planck. En assignant heuristiquement un bit d'information à une particule élémentaire, il devenait tentant d'affirmer que la surface d'un trou noir était une mesure de la quantité d'information absorbée par celui-ci, le nombre de bits d'information étant proportionnel au rapport de la surface du trou noir à la surface de Planck, ce qui correspond là encore à une définition de l'entropie en physique statistique.
Enfin, en parallèle à ces travaux s'est développée ce qui s'est finalement appelé la thermodynamique des trous noirs, c'est-à-dire un ensemble d'analogies frappantes entre des propriétés bien connues des systèmes thermodynamiques et les paramètres décrivant les trous noirs. En particulier, une des formulations de la thermodynamique indique que la variation dUde l'énergie interne s'exprime sous la forme d'une variation d'entropie dS sous la forme
- dU = TdS + ...,
où T représente la température du système, et où les points de suspension représentent d'autres termes éventuels qui dépendent du système considéré. Si l'on considère le trou noir le plus simple qui soit, un trou noir de Schwarzschild, alors la relation entre la masse M et la surface A de ce trou noir peut s'écrire
-
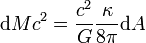
où κ est une quantité appelée gravité de surface, qui est une mesure de l'intensité du champ gravitationnel au voisinage du trou noir, et G la constante de gravitation. Le membre de gauche de cette équation représente une variation d'énergie (toujours par la formule E=mc²), qu'il est tentant d'identifier à la variation d'énergie interne en thermodynamique ordinaire, et par analogie, il est tentant d'identifier la surface du trou noir à une forme d'entropie. Cependant, là encore, rien de précis concernant la signification de la température associée au trou noir apparaît.
La solution à ces interrogations est venue en 1974 quand Stephen Hawking réussit à démontrer qu'en raison d'effets de mécanique quantique, les trous noirs rayonnaient. La forme de ce rayonnement est exactement celle d'un corps noir, c'est-à-dire d'un objet à l'équilibre thermique. De plus, Hawking calcula la température de ce rayonnement, qui se trouvait proportionnelle à la gravité de surface, comme suggéré par l'analogie thermodynamique déjà mentionnée. Ainsi, connaissant la valeur de la température, Hawking put proposer que les trous noirs possédaient une entropie, s'exprimant en termes de leur surface A par la formule
-
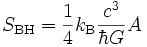
où kB est la constante de Boltzmann et

La formule ci-dessus est connue sous le nom de formule de Bekenstein-Hawking. Avant sa découverte du rayonnement qui porte son nom, Hawking s'était montré très sceptique quant à la possibilité suggérée par Bekenstein que la notion d'entropie des trous noirs puisse avoir un sens.

















































