Surjection - Définition

Une fonction est dite surjective ou est une surjection si pour tout y dans l'ensemble d'arrivée Y, il existe au moins un élément x de la source X tel que f(x) = y. On dit alors que tout élément y de Y admet au moins un antécédent x (par f).

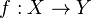
De façon équivalente, on dit que f est surjective si l'image directe est égale à l'ensemble d'arrivée Y, avec Df l'ensemble de définition de f.

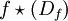
Quand X et Y sont tous les deux égaux à la droite réelle , alors une fonction surjective a un graphe qui intersecte toute droite horizontale.

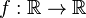
Si une surjection est aussi une injection, alors on l'appelle une bijection.

Définition formelle

Soit f une application de E dans F. f est dite surjective si et seulement si

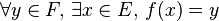
Exemple concret

Prenons le cas d'une station de vacances où un groupe de touristes doit être logé dans un hôtel. Chaque façon de répartir ces touristes dans les chambres de l'hôtel peut être représentée par une application de l'ensemble des touristes vers l'ensemble des chambres (à chaque touriste est associée une chambre).

• Les touristes souhaitent que l'application soit injective, c'est-à-dire que chacun d'entre eux ait une chambre individuelle. Cela n'est possible que si le nombre de touristes ne dépasse pas le nombre de chambres.
• L'hôtelier souhaite que l'application soit surjective, c'est-à-dire que chaque chambre soit occupée. Cela n'est possible que s'il y a au moins autant de touristes que de chambres.
• Ces desiderata ne sont compatibles que si le nombre de touristes est égal au nombre de chambres. Dans ce cas, il sera possible de répartir les touristes de telle sorte qu'il y en ait un seul par chambre, et que toutes les chambres soient occupées : l'application sera alors à la fois injective et surjective ; on dira qu'elle est bijective.

Exemples et contre-exemples

Fonctions sur les réels:

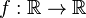
f(x) = x²

n'est pas surjective, car il n'y a pas de x tel que f(x) = -4, par exemple. En revanche, si on change la définition de f en donnant son ensemble d'arrivée comme étant R+, alors elle le devient.

Considérons la fonction définie par f(x) = 2x + 1. Cette fonction est surjective, puisque pour tout réel arbitraire y, nous pouvons trouver des solutions de l'équation y = 2x + 1 d'inconnue x; une solution est x = (y − 1)/2.

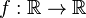
En revanche, la fonction définie par g(x) = (cos x)² n'est pas surjective, parce que (par exemple) il n'existe pas de réel x tel que (cos x)² = -1.

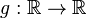
D'autre part, si nous définissons la fonction par la même relation que g, mais avec un ensemble d'arrivée qui a été restreint à l'ensemble des nombres réels compris entre 0 et 1, alors la fonction h est surjective. Cela s'explique par le fait que, pour tout réel arbitraire y de l'intervalle [0, 1], nous pouvons trouver des solutions de l'équation y = (cos x)² d'inconnue x qui sont par exemple x = Arccos(√y) ou x = Arccos(−√y).

Propriétés

• Une fonction f: X → Y est surjective si et seulement si il existe une fonction g: Y → X telle que f ? g soit égale à l'application identique sur Y. (cette proposition est équivalente à l'axiome du choix.)
• Une fonction est bijective si et seulement si elle est à la fois surjective et injective.
• Si f ? g est surjective, alors f est surjective.
• si f et g sont toutes les deux surjectives, alors f ? g est surjective.
• f: X → Y est surjective si et seulement si, pour toutes fonctions données g,h:Y → Z, lorsque g ? f = h ? f, alors g = h. En d'autres termes, les fonctions surjectives sont précisément les épimorphismes dans les catégories d'ensembles.
• Si f: X → Y est surjective et B est un sous-ensemble de Y, alors f(f ⁻¹(B)) = B. Ainsi, B peut retrouver à partir de l'image directe de f ⁻¹(B).
• Toute fonction h: X → Z peut être décomposée comme h = g ? f pour une surjection f et une injection g convenables. Cette décomposition est unique à un isomorphisme près, et f peut être considérée comme fonction prenant les même valeurs que h mais avec son ensemble d'arrivée restreint à l'image de h, h(X), qui est seulement un sous-ensemble de l'ensemble d'arrivée Z de h.
• Si f: X → Y est une fonction surjective, alors X a au moins autant d'éléments que Y, au sens des cardinaux. (cette proposition est aussi équivalente à l'axiome du choix.)