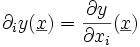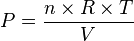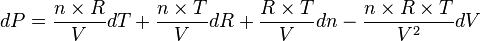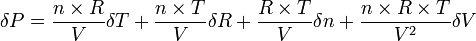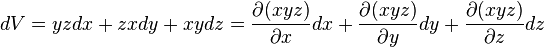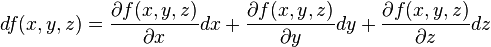Propagation des erreurs - Définition

Une mesure est toujours entachée d'erreur. Lorsqu'une valeur mesurée est utilisée dans une formule, il faut savoir estimer l'erreur induite sur le résultat de la formule. On parle de propagation d'erreur.

Approches pragmatiques

Report des extrêmes dans le calcul

La première solution consiste à effectuer les calculs avec les extrêmes de l'intervalle d'erreur. Si la mesure a pour valeur

a ± Δa

alors la " valeur réelle " est supposée être dans l'intervalle [a-Δa;a+Δa]. On calcule donc ici

y₁ = ƒ(a-Δa)

y₂ = ƒ(a+Δa)

et, selon l'ordre de y₁ et de y₂, on prend [y₁;y₂] ou [y₂;y₁] comme intervalle d'erreur.

Cette méthode n'est valable que si la loi est monotone (c'est-à-dire croissante ou décroissante) sur l'intervalle [a-Δa;a+Δa].

Estimation à partir de la dérivée

Une manière simple, utilisée fréquemment en physique, consiste à utiliser un développement limité du premier ordre, c'est-à-dire à remplacer la loi ƒ par sa " tangente " pour estimer l'erreur. On estime ainsi l'erreur avec une loi uniforme (linéaire) et simple.

On a  :

ƒ(x) = ƒ(a) + ƒ '(a)·(x-a) + o(x)

où o(x) est une fonction qui " tend vite " vers 0. Si l'on remplace x par a + Δa, on a alors

ƒ(a + Δa) = ƒ(a) + ƒ '(a)·Δa + o(a + Δa)

On peut donc estimer

Δy ≈ ƒ '(a) · Δa

Cette erreur est sous-estimée si l'on a une loi convexe.

Approche mathématique

Notations

• x une variable aléatoire,
• E(x) ou <x> l'espérance mathématique de x,
• V(x) la variance de x.
• est la dérivée partielle de la fonction y par rapport à la i ^e variable.

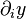
par exemple, si x est un vecteur (x₁, x₂,…, x_n), alors

Formules

Une fonction de variables aléatoires

est elle-même une variable aléatoire. Si les erreurs sont petites, la variance du développement limité de y au premier ordre autour des valeurs moyennes μ des x est une bonne estimation de la variance de y :

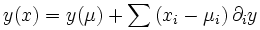
On néglige les termes d'ordre supérieur dans l'expansion, il vient :

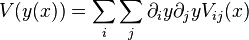
Si les x sont indépendantes

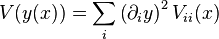
Applications

Mesure d'une résistance

Une application pratique est la mesure expérimentale d'une résistance R à partir de la chute de tension U entre ses bornes et du courant I. La résistance est décrite par la loi d'Ohm.

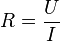
Nous avons

et

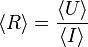
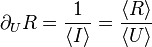
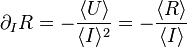
Il vient

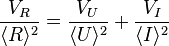
Dans ce cas simple, l'erreur relative sur R correspond à la moyenne géométrique des erreurs relatives sur U et I.

Utilisation des différentielles totales exactes

Une loi physique s'exprime par une relation algébrique entre un cerain nombre de grandeurs mesurables :

• P : pression du gaz
• V : volume occupé par le gaz
• n : quantité de gaz en moles (1 mole = 6,022·10²³ molécules)
• R : constante des gaz parfaits = 8,314 J·K^-1·mol^-1
• T : température absolue du gaz, en kelvin

La pression en fonction de n, R, T et V s'exprime par

écrivons sa différentielle :

Si l'on " remplace " des variations élémentaires de variables dx par les erreurs sur les variables δx, on obtient :

qui donne l'erreur absolue sur P déduite du calcul de P à partir de la connaissance des erreurs sur T, R, n et V.

Autres exemples simples :

• le calcul de la surface d'un rectangle.

S = Ll et S + dS = (L + dL)(l + dl) = Ll + Ldl + ldL + dldL

peut s'écrire

dS = ((L + dL)(l + dl) − Ll) = Ldl + ldL + dLdl

que l'on approxime par

dS = Ldl + ldL

• le calcul d'un volume V = x·y·z

V(x + dx,y + dy,z + dz) = (x + dx)(y + dy)(z + dz) = xyz + dxyz + xdyz + xydz + xdydz + ydxdz + zdxdy + dxdydz

peut s'écrire

dV = yzdx + zxdy + xydz + dxdydz

que l'on approxime par dV = yzdx + zxdy + xydz

noter que

rappel:

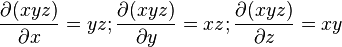
• et plus généralement pour le calcul de la variation d'une fonction ƒ(x,y,z).

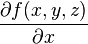
si est la dérivée partielle par rapport à x