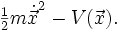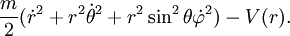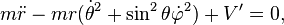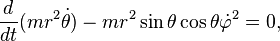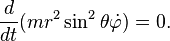Action (physique) - Définition
En physique théorique, l’action est une grandeur physique scalaire ayant pour dimension le produit d'une énergie par un temps.
Par exemple, le moment cinétique est une action.
Principe de moindre action
Énoncé
L'importance de l'action en physique est due à l'existence d'un principe très général, appelé principe de moindre action : le trajet effectivement suivi par un objet entre deux points donnés est celui qui conduit à une valeur stationnaire de l’action. Lorsque les points sont proches, cet extremum de l'action est un minimum, d'où le nom donné au principe.
Commentaires
Par exemple, en mécanique, au lieu de penser accélération sous l’effet de forces, on raisonne en terme de chemin d’action stationnaire.
Ce principe de moindre action s’est avéré simple, puissant et général à la fois en mécanique classique où il est strictement équivalent aux lois de Newton et en mécanique quantique ou relativiste et en électromagnétisme où sa généralisation a été très fructueuse .
Beaucoup de problèmes de physique peuvent être résolus en partant de ce principe :
- que ce soit pour trouver le trajet du maître nageur pour atteindre le plus rapidement une personne en train de se noyer ou pour trouver le parcours de la lumière ou le trajet dans un champ gravitationnel d’un point à un autre .
- que se soit pour établir les équations de Maxwell ou les bases de la mécanique quantique dans la formulation de Feynman en intégrale de chemin.
Les symétries d’une situation physique peuvent être mieux traitées, par exemple en utilisant le théorème de Noether qui établit qu’à toute symétrie continue correspond une loi de conservation.
D’abord formulé par Pierre Louis Moreau de Maupertuis, puis développé par Euler et Leibniz (Pierre de Fermat avait déjà établi un principe de moindre temps pour le trajet de la lumière), le principe de moindre action avait conduit à la formulation Lagrangienne et Hamiltonienne de la mécanique classique.
Ce principe est un des plus importants principes de base de la physique.
Formalisation
Un lagrangien
![\mathcal{L}[\varphi_i]](https://static.techno-science.net/illustration/Definitions/autres/b/b9c3f5e4b34fb0ba13145ec0678fb4d3_0d96029bf6d1d17aca907479493ef72f.png)
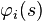
Les équations du mouvement s’obtiennent selon le principe d’action stationnaire en écrivant que :
|
|
où l’action est :
|
|
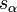
Les équations du mouvement obtenues ainsi sont identiques aux équations d’Euler Lagrange, et sont appelées un système dynamique Lagrangien
Les exemples de systemes dynamiques Lagrangiens vont du Modèle standard aux équations de Newton à des problèmes de mathèmatiques pures tels que les équations géodésiques
Un exemple de mécanique classique
La mécanique Lagrangienne est une reformulation de la mécanique classique; le Lagrangien est :
l’énergie cinétique – l’énergie potentielle
Alors l’équation de Euler-Lagrange est

Où les dérivées par rapport au temps sont écrites avec des points situés au-dessus de ce qui doit être dérivé
L’on voit immédiatement que ce n’est autre que si on considère que l’ equation
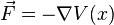
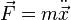
Une autre approche nous donnerait
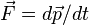
En coordonnées sphériques : r, θ, φ le Lagrangien s’écrit :
Et les équations d’ Euler-Lagrange :
Dans ce cas le paramètre
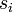
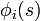
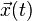
voir aussi
- Principe de moindre action
- Mécanique lagrangienne
- Théorème de Noether
- Mécanique hamiltonienne
- Action d'Einstein-Hilbert
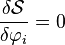
![\mathcal{S}[\varphi_i] = \int{\mathcal{L}[\varphi_i(s)]{}\,d^ns},](https://static.techno-science.net/illustration/Definitions/autres/6/6d1ddad9e9382dec25e2d70071bb51e5_68b4e8d30c0281cf71504c9b8043e195.png)