Compas (géométrie) - Définition
Un compas est un instrument de construction géométrique qui sert à comparer et à reporter des distances. Le verbe latin compassare signifiait " mesurer avec ses pas ".
Un compas est composé de deux éléments articulés en un point.
Les compas sont classifiés en fonction de leurs caractéristique de conception ou par leurs usages.
Classification par conception
Type de pointe
Un compas comporte systématiquement une pointe représentant le centre du cercle. L’autre pointe comporte soit un crayon soit une autre pointe, le compas est dit alors à " pointe sèche ". Le crayon permet de tracer des cercles ou des arc de cercle. Les compas à pointe sèche sont utilisés soit pour marquer par une légère rayure un cercle ou arc de cercle dans un matériau ou pour reporter une longueur. Le compas à pointe sèche est généralement utilisé par les usineurs, les charpentiers, les ébénistes ou les tailleurs de pierre etc pour mesurer ou reporter des dimensions.
| Compas à crayon. Ce compas comporte une rallonge. | Compas porte crayon. Ce compas permet d’adapter divers crayons. Il est ici équipé d’un stylo à encre de dessinateur. | Compas à pointe sèche. |
|---|---|---|
Compas à charnière
C’est le compas le plus simple. Il est constitué de deux bras articulés autour d’une charnière. Il est parfois équipé d’un secteur permettant de le bloquer par une vis dans une position donnée. En fonction de la dimension du secteur, il peut être appelé compas 1/4 de cercle.
| Compas à charnière simple en fer forgé. XVIIIe siècle | Compas à secteur |
|---|---|
|
|
Compas à ressort
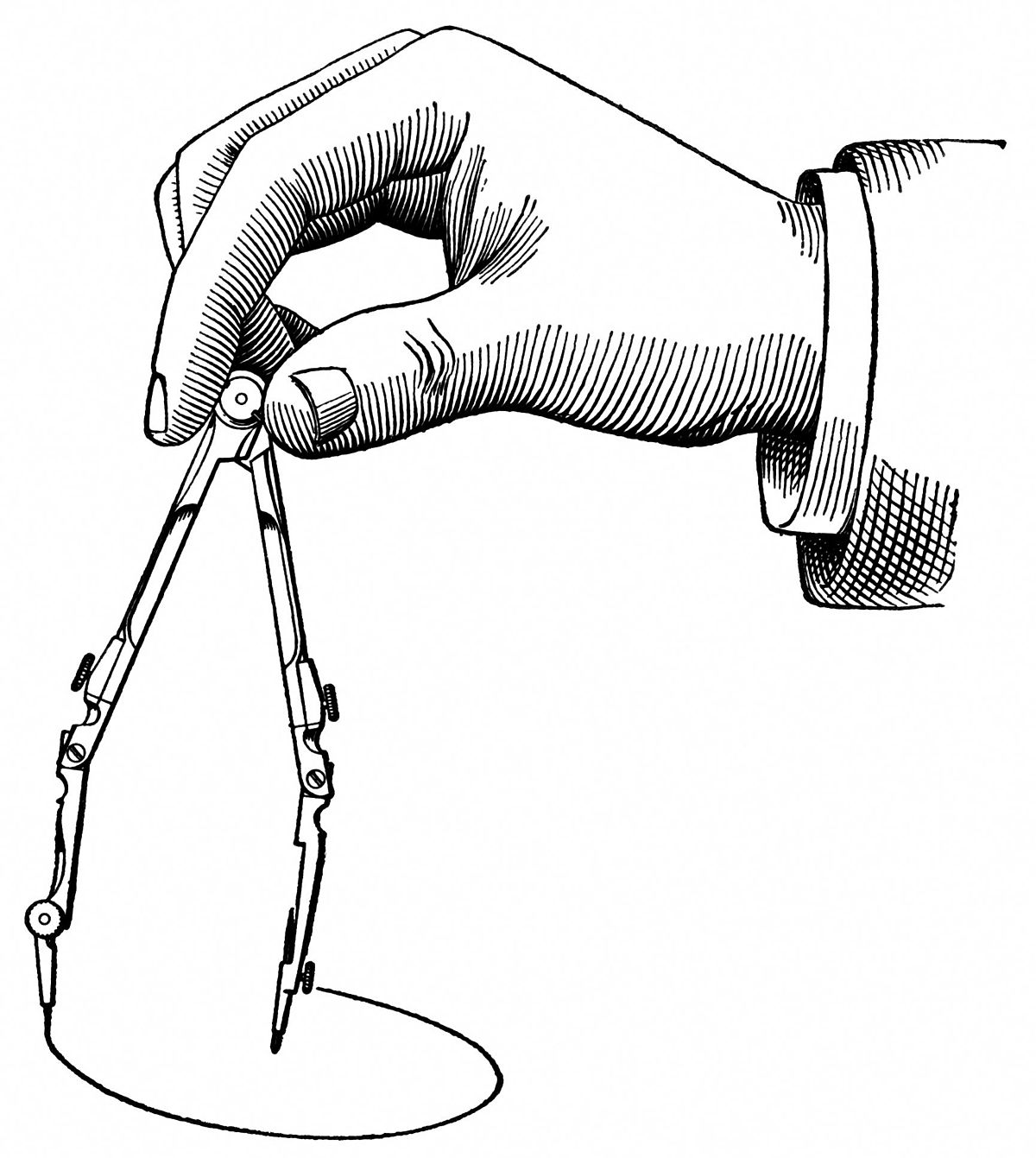
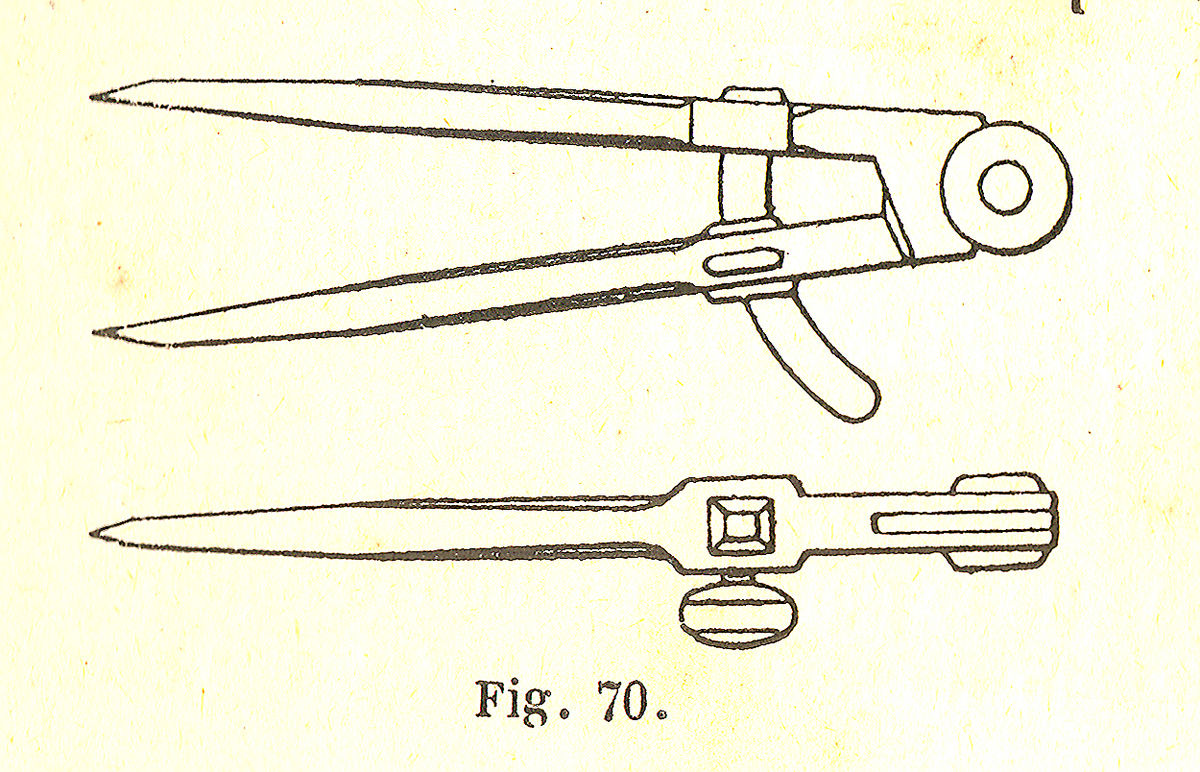
L’articulation du compas est équipée d’un ressort qui écarte les deux bras. Le compas est réglé à l’aide d’une vis et d’une molette qui permet de le bloquer dans une position donnée. La précision est meilleure que pour les compas à articulation. On l'appelle aussi compas à balustre.
| Compas à ressort moderne à crayon | Compas à ressort (représentation du XIXe siècle) |
|---|---|
|
|
Classification par usage
Le compas droit
C’est la forme la plus simple et la plus classique de compas. Les deux branches sont droites.
| Compas droit à charnière | Compas droit à ressort et à pointe sèche |
|---|---|
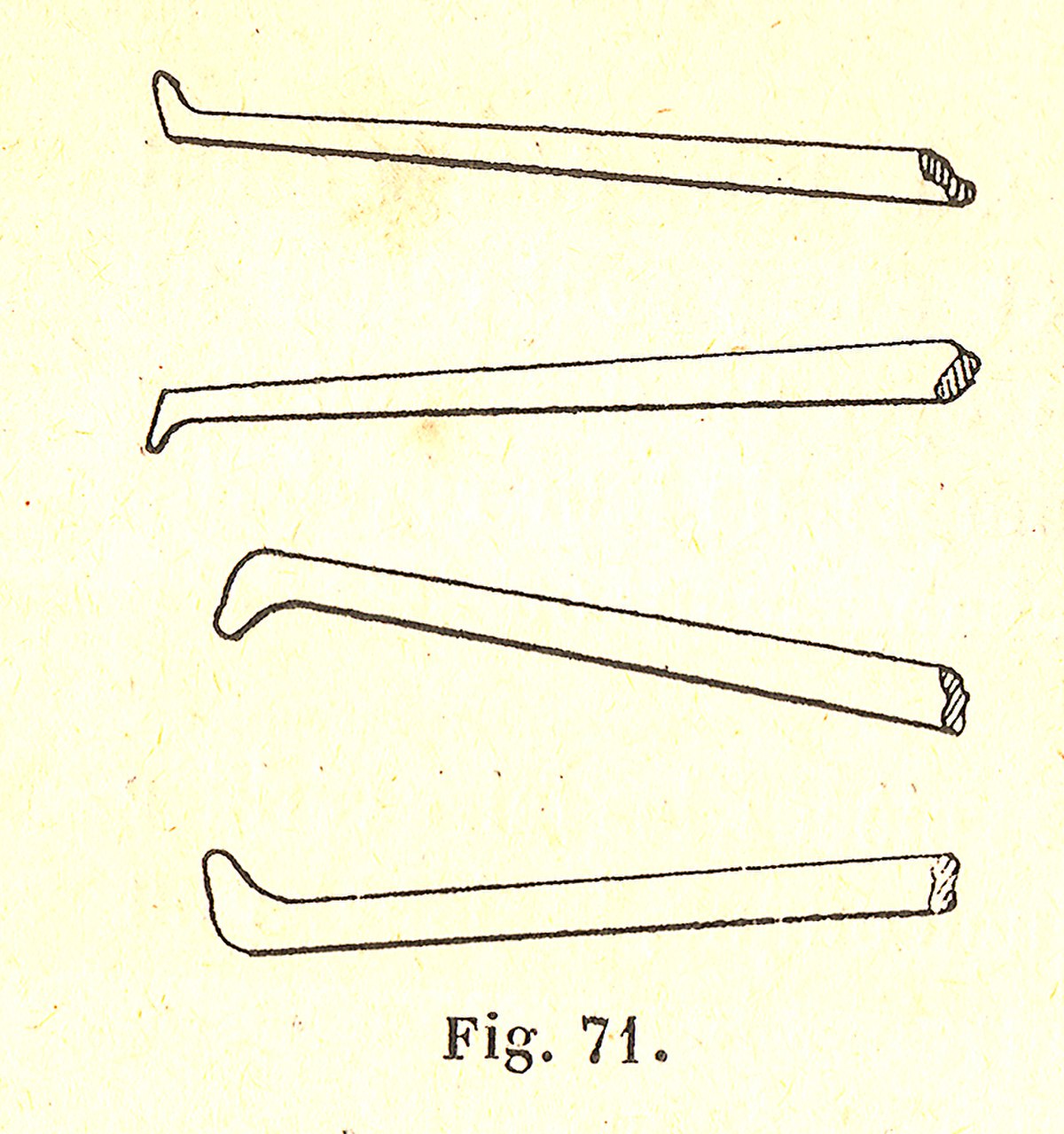
Compas d’épaisseur
Le Compas d'épaisseur est un outil de traçage qui permet de relever une cote, pour transférer des mesures ou contrôler des épaisseurs. Ses deux bras ont une forme caractéristique qui évite d’être gêné quand l’opérateur effectue la mesure.
| Compas d’épaisseur à ressort | Compas d’épaisseur à secteur |
|---|---|
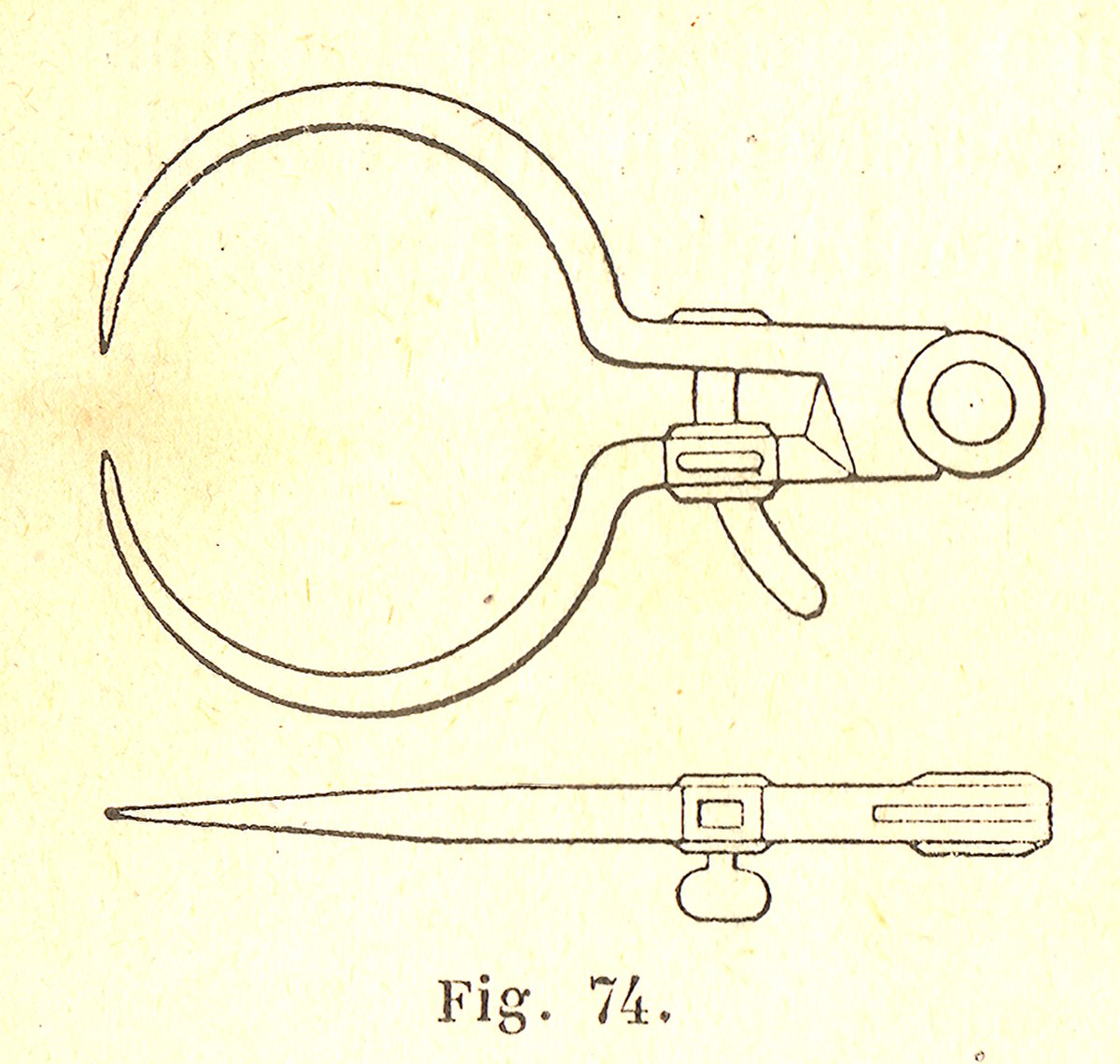
Compas d’intérieur
nommé aussi maître à danser
Le compas d’intérieur a un usage similaire au compas d’épaisseur. Il permet de mesurer ou de reporter la dimension d’un diamètre intérieur comme un alésage.
| Compas d’intérieur à ressort | détail de l'extrémité |
|---|---|
Compas à verge
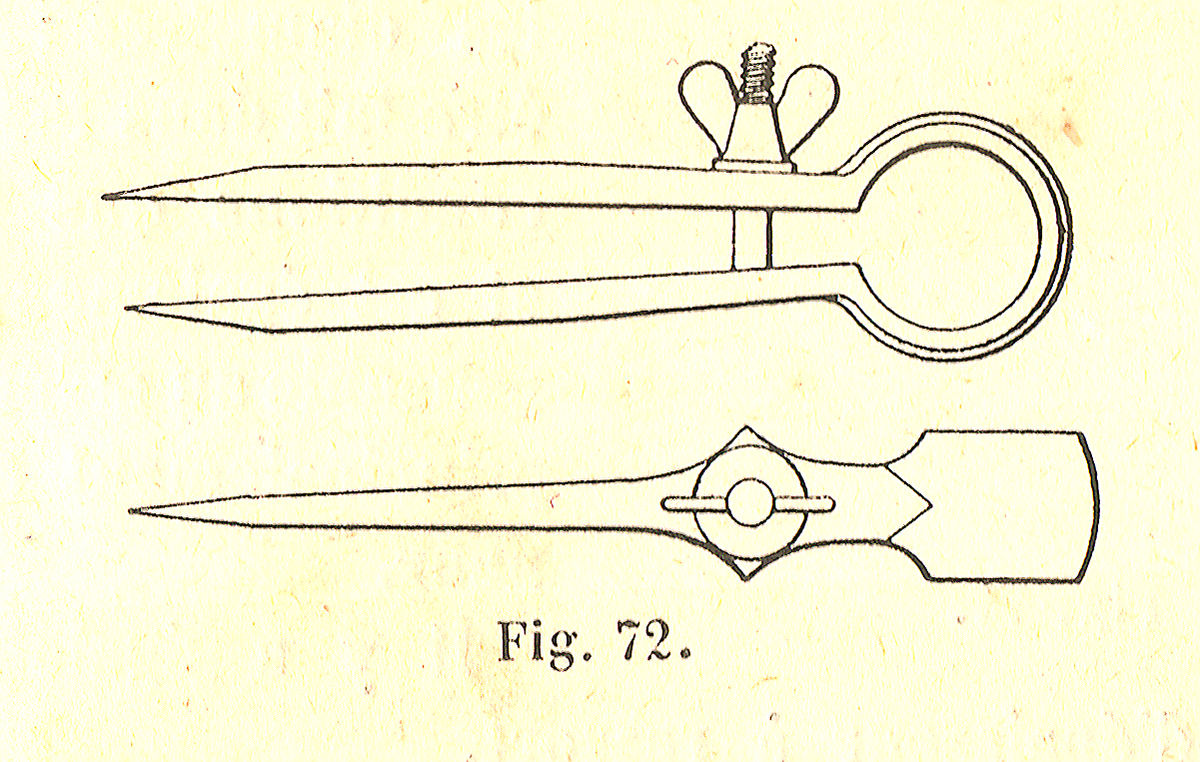
Le compas à verge est une sorte de compas composé de deux coulisseaux positionnables sur une bande (verge) et portant chacun une pointe sèche, un porte mine, un tire-ligne, ou similaire. Son usage est identique à celui d'un compas de géométrie classique, mais adapté aux grandes dimensions: il est en fait limité par la longueur de la verge.
| Compas à verge | Représentation du XIXe siècle |
|---|---|
Compas de transfert
Le compas de transfert est un outil utilisé pour transférer les contours d'une forme sur une autre forme.
Sans compas?
En géométrie le compas sert à reporter des longueurs dans n'importe quelle direction, d'où le traçage de cercles, la construction d'angles droits, du milieu, de la médiatrice. On pourrait se demander: est-il possible de faire de la géométrie sans compas?
- La réponse est oui! La géométrie sans compas, avec juste la règle non-graduée s'appelle la géométrie projective et a donné lieu à des théorèmes remarquables comme le théorème de Pascal, le théorème de Pappus, le théorème de Desargues, le théorème d'Hessenberg.