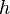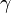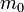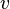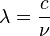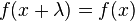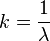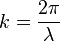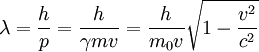Longueur d'onde - Définition
La longueur d'onde d'une onde électromagnétique périodique est la distance que parcourt la lumière dans le vide pendant le temps qui sépare deux crêtes successives de cette onde électromagnétique. On la dénote communément par la lettre grecque λ (lambda).
où :
- λ = longueur d'onde de l'onde
- c = vitesse de la lumière (3×108 m/s)
- ν = fréquence de l'onde
Pour aller plus loin...
La longueur d'onde est la distance séparant deux crêtes successives d'une onde périodique. On la dénote communément par la lettre grecque λ (lambda). Mathématiquement, on peut la définir ainsi : si l'onde peut être représentée par une fonction périodique f qui prend comme argument la distance x, alors la longueur d'onde est le plus petit λ > 0 tel que pour tout x, on ait:
Par analogie avec la notion mathématique homonyme, on la dénomme aussi parfois improprement période. En physique, la période est l'équivalent temporel de la longueur d'onde : la période est le temps minimal qui s'écoule entre deux répétitions identiques de l'onde en un même point. Pour une onde sinusoïdale, la longueur d'onde est la distance entre deux pics de même signe successifs :
L'axe x représente les distances parcourues, et y est la valeur à un instant donné d'une quantité qui varie (par exemple la pression de l'air pour une onde sonore ou l'intensité du champ électrique ou magnétique d'une onde lumineuse).
La longueur d'onde est proportionnelle à la période, et donc inversement proportionnelle à la fréquence, le nombre de sommets de même signe qui traversent un point en une durée d'une seconde. La longueur d'onde est égale à la vitesse de l'onde divisée par la fréquence de passage. Lorsque l'on est dans le cas d'une onde électromagnétique se propageant dans le vide, cette vitesse est la vitesse de la lumière c dans le vide, et la relation s'écrit
où :
- λ = longueur d'onde de l'onde
- c = vitesse de la lumière (3×108 m/s)
- ν = fréquence de l'onde
Pour les ondes radio, cette formule se calcule facilement : longueur d'onde (en mètres) = 300 / fréquence (en Mégahertz)
Le nombre d'onde est l'inverse de la longueur d'onde:
c'est le nombre de cycles (d'" ondes ") que l'on a dans un mètre. Le nombre d'onde est également parfois défini par
pour simplifier les expressions.
Exemple de longueur d'onde
| Longueur d'onde | Domaine | Commentaire |
|---|---|---|
| > 10 cm | radio | (150 kHz - 3 GHz) |
| de 1 mm à 10 cm | micro-onde et radar |
(10 cm - +- 1cm, 3 - 300 GHz) |
| de 1 µm à 500 µm | infrarouge norme nf/en 1836 | |
| de 400 nm à 700 nm | lumière visible | rouge (620-700 nm) orange (592-620 nm) jaune (578-592 nm) vert (500-578 nm) bleu (446-500 nm) violet (400-446 nm) |
| de 10 nm à 400 nm de 10-8 m à 10-7 m |
ultraviolet |
(400 - 280 nm) |
| de 10-11 m à 10-8 m | rayon X | |
| de 10-14 m à 10-12 m | rayon γ |
Longueur d'onde de Broglie
Louis de Broglie a découvert que toutes les particules physiques dotées d'une quantité de mouvement ont une longueur d'onde, nommée longueur d'onde de Broglie (voir l'article Mécanique ondulatoire). Pour une particule relativiste, la longueur d'onde de Broglie est donnée par
où 
est la constante de Planck, 
le facteur de Lorentz, 
la masse de la particule au repos, 
la vitesse, et 
la vitesse de la lumière dans le vide.