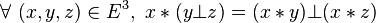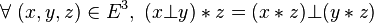Loi de composition interne - Définition
L’algèbre est la branche des mathématiques qui s’intéresse aux ensembles et aux opérations qui peuvent s’y effectuer. Elle recherche les conséquences générales qui découlent des propriétés de ces opérations, indépendamment de la nature précise des ensembles et des opérations en cause. Parmi les opérations étudiées, les lois de composition interne occupent une place privilégiée.
Présentation
On nomme loi de composition interne dans un ensemble une opération qui prend deux éléments de l’ensemble pour donner un résultat dans ce même ensemble. Ainsi, l’addition ou la multiplication sont des lois de composition interne dans tout ensemble dont le résultat de l'addition ou de la multiplication sont un élément.
Pour que l’opération considérée soit effectivement une loi de composition interne, il faut qu’elle ait un sens quels que soient les deux éléments de l’ensemble choisis (on dit formellement que l’opération doit être définie partout). Ainsi :
- la division n’est pas une loi de composition interne dans

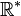
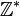
- la soustraction peut être ou non une loi de composition interne selon l’ensemble de nombres considéré :
- s’il s’agit de l’ensemble des nombres usuels, dits entiers naturels { 0, 1, 2, 3,... }, ce n’en est pas une, puisque " 3 - 5 ", par exemple, n’a pas pour résultat l’un de ces nombres usuels.
- si au contraire, on choisit l’ensemble des entiers relatifs, qui en plus des entiers naturels, contient les entiers négatifs { -1, -2, -3,... }, alors la soustraction est bien une loi de composition interne.
Exemple
Dans l’ensemble des entiers relatifs, l’addition est une loi de composition interne ayant entre autres les propriétés suivantes, qui seront définies plus formellement dans la seconde partie de l’article :
- zéro est élément neutre pour cette loi : l’ajouter à n’importe quel nombre redonne ce nombre : par exemple, 5 + 0 = 5 , et 0 + 8 = 8 ;
- pour tout entier, il existe un autre nombre, son opposé (le terme général est élément symétrique), tel qu’ajouté au premier, il redonne l’élément neutre, zéro. L’opposé se note comme l’entier initial changé de signe. Ainsi : 3 + (-3) = 0 ;
- on peut échanger les deux éléments autour du signe " + " : 3 + 5 = 5 + 3 = 8 . On dit que l’opération est commutative ;
- on peut grouper les éléments comme on le souhaite quand on en ajoute plus de deux : 3 + 5 + 4 peut se calculer de deux manières :
- en calculant d’abord 3 + 5 = 8 puis en ajoutant 4 au résultat,
- ou en calculant 5 + 4 = 9 avant de calculer 3 + 9 .
- Ces deux méthodes mènent au même résultat, ce que l’on note : (3 + 5) + 4 = 3 + (5 + 4) . On dit que l’opération est associative.
Ces quatre propriétés, existence d’un élément neutre, existence de symétriques, commutativité, associativité, peuvent se retrouver pour d’autres ensembles et d’autres lois. Ainsi, on peut étudier l’ensemble des translations (c’est-à-dire les déplacements en ligne droite : par exemple, se déplacer de 3 mètres vers la gauche et de 2 mètres vers le haut), et une loi de composition interne sur cet ensemble, la composition : la composition de deux translations consistant simplement à faire le premier déplacement, puis le second. On retrouve pour la composition les mêmes propriétés que pour l’addition :
- le neutre est la translation nulle, consistant à ne pas se déplacer ;
- le symétrique d’une translation consiste à faire le même déplacement dans l’autre sens (3 mètres à droite et 2 mètres vers le bas pour l’exemple précédent) : si on fait successivement les deux, c’est comme si on faisait le déplacement nul ;
- on peut faire les déplacements dans l’ordre qu’on veut, on retrouve la commutativité et l’associativité.
L’ensemble des entiers relatifs avec l’addition, et l’ensemble des translations avec la composition ont ces propriétés simples en commun. Un ensemble et une loi qui possèdent ces quatre propriétés particulières s’appelle en algèbre un groupe abélien. L’algèbre s’attache ensuite à rechercher d’autres propriétés plus complexes qui découlent de ces quatre premières. Ces nouvelles propriétés seront alors valables aussi bien pour l’ensemble des entiers relatifs que pour celui des translations, et pour tout autre ensemble et tout autre loi de composition interne ayant la structure d’un groupe abélien, sans qu’il soit nécessaire de le redémontrer pour chacun.
Définition formelle
On appelle loi de composition interne sur un ensemble E toute application

Un ensemble E muni d’une loi de composition interne


Quelques exemples triviaux, pour un ensemble E non vide :
- les applications constantes : si c appartient à E :

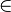

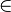
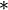
- l’application sélectionnant le terme de gauche :

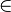

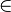
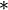
- l’application sélectionnant le terme de droite :

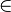

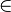
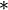
Éléments particuliers
Carrés et dérivés
Dans un magma ( E,

- un élément

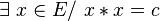
- En sens inverse, tout élément x a un carré unique, noté habituellement " x 2 ".
- un élément

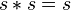
- En d’autres termes, cet élément est son propre carré.
- un élément
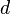
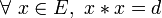
- En d’autres termes, d est le carré de tous les éléments de E. Tout élément dévolutif est idempotent. En effet, il est carré de tout élément de E donc en particulier, il est son propre carré
Neutres et dérivés
- un élément

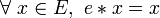
- un élément

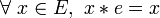
- un élément

- Tout élément neutre, même unilatère (c’est-à-dire soit à gauche, soit à droite, mais pas les deux), est idempotent.
- un élément


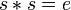
- L’élément neutre est nécessairement involutif.
- Le seul élément involutif et idempotent est l'élément neutre.
Absorbants et dérivés
- un élément

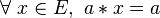
- un élément

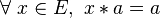
- un élément

- Tout élément absorbant, même unilatère, est idempotent.
- un élément


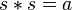
- L’élément absorbant est nécessairement nilpotent...
Centre d'une structure
- un élément

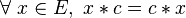
- Les éléments neutre et absorbant bilatères sont commutatifs.
- On appelle centre de E, et on note Z ( E ), l’ensemble des éléments commutatifs de E.
Réguliers et dérivés
- un élément

- un élément

- un élément

- un élément

- un élément

- un élément

- un élément

- un élément



- Un diviseur de zéro à gauche est irrégulier à gauche;
- un élément



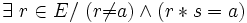
- Un diviseur de zéro à droite est irrégulier à droite;
Paires d'éléments
Des paires d’éléments peuvent aussi présenter des propriétés particulières :
- deux éléments



- deux éléments permutables


- - s’il existe un élément neutre

- - et si :
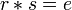
- deux éléments permutables


- - s’il existe un élément absorbant

- - si aucun des deux éléments n’est égal à

- - et si :
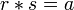
- Les diviseurs de zéro sont irréguliers. Les éléments nilpotents autres que l’élément absorbant sont des diviseurs de zéro.
Exemple: pour les entiers relatifs, 0 est neutre pour l’addition, absorbant pour la multiplication, et neutre à droite pour la soustraction.
Propriétés
Certaines propriétés des lois de composition interne, particulièrement intéressantes, ont reçu un nom. Soit un magma ( E,


Existence d’éléments remarquables
-


-
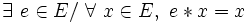
- Une loi peut présenter plusieurs éléments neutres à gauche, à condition qu’elle ne présente pas d’élément neutre à droite;
-


-
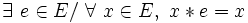
- Une loi peut présenter plusieurs éléments neutres à droite, à condition qu’elle ne présente pas d’élément neutre à gauche;
-


-
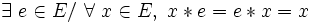
- Une loi est unifère si et seulement si elle est unifère à gauche et unifère à droite;
- L’élément neutre d’une loi unifère est unique;
-


-
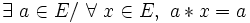
- Une loi peut présenter plusieurs éléments absorbants à gauche, à condition qu’elle ne présente pas d’élément absorbant à droite;
-


-
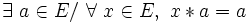
- Une loi peut présenter plusieurs éléments absorbants à droite, à condition qu’elle ne présente pas d’élément absorbant à gauche;
-


- Une loi est absorbante si et seulement si elle est absorbante à gauche et absorbante à droite;
- L’élément absorbant d’une loi absorbante est unique;
-

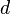
-
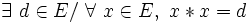
- L’élément dévolutif d’une loi dévolutive est unique;
-

-
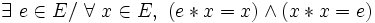
- Une loi est involutive à gauche si et seulement si elle est unifère à gauche et dévolutive, et l’élément neutre à gauche est l’élément dévolutif.
-

-
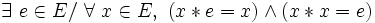
- Une loi est involutive à droite si et seulement si elle est unifère à droite et dévolutive, et l’élément neutre à droite est l’élément dévolutif.
-

-
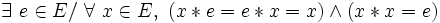
- Une loi est involutive si et seulement si elle est unifère et dévolutive, et l’élément neutre est l’élément dévolutif.
-

-
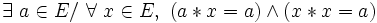
- Une loi est nilpotente à gauche si et seulement si elle est absorbante à gauche et dévolutive, et l’élément absorbant à gauche est l’élément dévolutif.
-

-
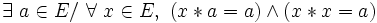
- Une loi est nilpotente à droite si et seulement si elle est absorbante à droite et dévolutive, et l’élément absorbant à droite est l’élément dévolutif.
-

-
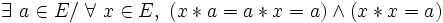
- Une loi est nilpotente si et seulement si elle est absorbante et dévolutive, et l’élément absorbant est l’élément dévolutif.
-

-

Régularité et propriétés liées
-

-

-

-
![\forall\ ( x , y , z ) \in E^3 ,\ [\ ( x * y = x * z ) \or ( y * x = z * x )\ ] \Rightarrow ( y = z ) \,](https://static.techno-science.net/illustration/Definitions/autres/9/9ed02e073a2234a03f483f19f7b9393d_2aa1c88204a0005b8938db3cbbe5e928.png)
- Une loi est régulière si et seulement si elle est régulière à gauche et régulière à droite;
- On peut noter que si


-

-



-
![\forall\ ( a , b ) \in E^2 , [\ \exists\ x \in E /\ ( a * x = b ) \wedge [\ \forall\ z \in E ,\ ( a * z = b ) \Rightarrow ( z = x ) ] ] \,](https://static.techno-science.net/illustration/Definitions/autres/4/46c4653a7e1f760acbec44a4fc774edf_964428e6a66da291b3468bdfe111335b.png)
-
- Cette propriété est plus forte que la régularité : toute loi symogène est nécessairement régulière;
Associativité et propriétés analogues
-

-
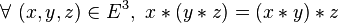
- On peut noter que l’associativité d’une loi permet de se passer des parenthèses quand on répète la loi; on peut noter aussi que la plupart des lois intéressantes sont associatives (exemples : l’addition, la multiplication, la composition des correspondances,...).
-

-
![\forall\ ( x , y ) \in E^2 ,\ [\ x * ( x * y ) = ( x * x ) * y \ ] \wedge [\ ( x * y ) * y = x * ( y * y )\ ] \,](https://static.techno-science.net/illustration/Definitions/autres/4/431b392eef9f32a1027086554df87af5_101eeccbb363294087783992fe6f9036.png)
- Cette propriété est moins forte que l'associativité, puisqu’une loi associative est nécessairement alternative.
-

-
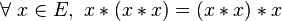
- Cette propriété est moins forte que l’alternativité, puisqu’une loi alternative est nécessairement associative des puissances.
- Quand cette propriété est vérifiée, il est possible d’introduire la notion de puissance d’un élément (d’où le nom de la propriété) :
- - la puissance n-ième d’un élément x, notée habituellement " x n ", est égale au résultat de la composition de x selon




- - si, de plus, la loi

- - la puissance n-ième d’un élément x, notée habituellement " x n ", est égale au résultat de la composition de x selon
-

-
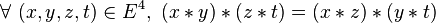
- Cette propriété est appelée permutativité car elle permet de permuter les termes moyens dans les expressions du type ci-dessus.
- Cette propriété est moins forte que l’associativité, car une loi associative et commutative est nécessairement permutative; notons toutefois qu’une loi associative, mais non-commutative, n’est pas nécessairement permutative, et qu’une loi permutative, même commutative, n’est pas nécessairement associative.
- (Exemples de lois permutatives non associatives : la soustraction dans

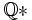
-

-
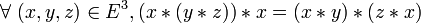
- Cette propriété est moins forte que l’associativité, puisqu'une loi associative est nécessairement neutroactive.
Autres propriétés
-

-

-
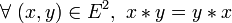
- Les lois commutatives sont notées par " + ", "
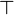


- Les notions de permutativité et de commutativité sont des notions différentes: il existe des lois permutatives et non commutatives (comme la soustraction dans

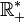
La liste de propriétés ci-dessus n’est pas exhaustive. Toutefois, nous n’en indiquerons ici qu’une autre : dans des structures algébriques comportant plusieurs lois, certaines de ces lois ont des propriétés relatives à d’autres lois. La plus importantes de ces lois relatives est la distributivité.
- Une loi


Cette propriété se décompose en deux parties :
- - distributivité à gauche :
-
- - distributivité à droite :
-
Remarque : si dans la situation ci-dessus la loi


Inversibilité
Cette propriété importante mérite un paragraphe séparé. Nous nous placerons dans un magma ( E,


- un élément

-
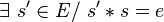
- s' est alors appelé élément symétrique à gauche de s;
- un élément

-
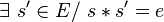
- s' est alors appelé élément symétrique à droite de s;
- un élément

- s' est alors appelé élément symétrique de s;
- la loi

- la loi

- la loi

Si la loi

Exemples :
- 2 n'est pas symétrisable pour l'addition dans les entiers naturels;
- 2 est symétrisable, de symétrique -2, pour l’addition dans les entiers relatifs;
- 2 n’est pas inversible pour le produit dans les entiers relatifs;
- 2 est inversible, d’inverse

Remarque :
- Lorsque la loi est notée additivement, le symétrique est plutôt appelé opposé, et quand la loi est notée multiplicativement le symétrique est plutôt appelé inverse.
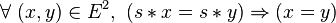
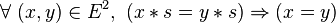
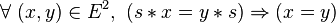
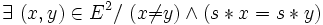
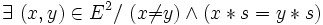
![\exists\ a \in E /\ \forall\ x \in E ,\ ( x * a = a * x = a ) \wedge [\ \forall\ y \in E ,\ ( x * y = a ) \Rightarrow ( x = a \vee y = a ) \ ] \,](https://static.techno-science.net/illustration/Definitions/autres/e/e2373a9510ceaa7a95db98de50d91851_b6a1e979e9bb61c03f0e8d08591203e7.png)
![\exists\ e \in E /\ \forall\ x \in E ,\ ( x * e = e * x = x ) \wedge [\ \forall\ y \in E ,\ ( x * y = e ) \Rightarrow ( x = e \vee y = e ) \ ] \,](https://static.techno-science.net/illustration/Definitions/autres/e/ecdc516f051508706d8a912500259f4f_e9bc99ef86519b2daa37d97fa2882fc8.png)
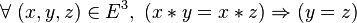
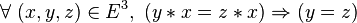
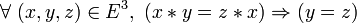
![\wedge [\ \exists\ y \in E /\ ( y * a = b ) \wedge [\ \forall\ z \in E ,\ ( z * a = b ) \Rightarrow ( z = y )\ ] ] \,](https://static.techno-science.net/illustration/Definitions/autres/6/6dd3b8f08f572a8ba62cd5ea8fbfa3f7_811d410a4b55bf66bbd5c4423ee295af.png)
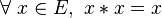
![\forall\ ( x , y , z , t ) \in E^4 ,\ ( x \bot y ) * ( z \bot t ) = [ ( x * z ) \bot ( x * t ) ]\ \bot\ [ ( y * z ) \bot (y * t ) ] \,](https://static.techno-science.net/illustration/Definitions/autres/4/4f1a20433cfa3a425732ea0050a34e16_9f495b81e666d823077727b1750bf0a7.png)