Bouteille de Klein - Définition
En mathématiques, la bouteille de Klein est une surface fermée, sans bord et non orientable, c'est-à-dire une surface pour laquelle on ne peut pas définir un " intérieur " et un " extérieur ". La bouteille de Klein a été décrite pour la première fois en 1882 par le mathématicien allemand Felix Klein. Elle est étroitement liée au ruban de Möbius et à des plongements du plan projectif réel tels que la surface de Boy.
C'est un des exemples les plus simples de variété abstraite, car c'est une surface qui ne peut être représentée convenablement dans l'espace à trois dimensions
Construction
La bouteille de Klein n'est pas réalisable dans
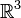
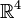
Voici un plan de montage dans
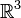
|
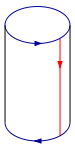
|
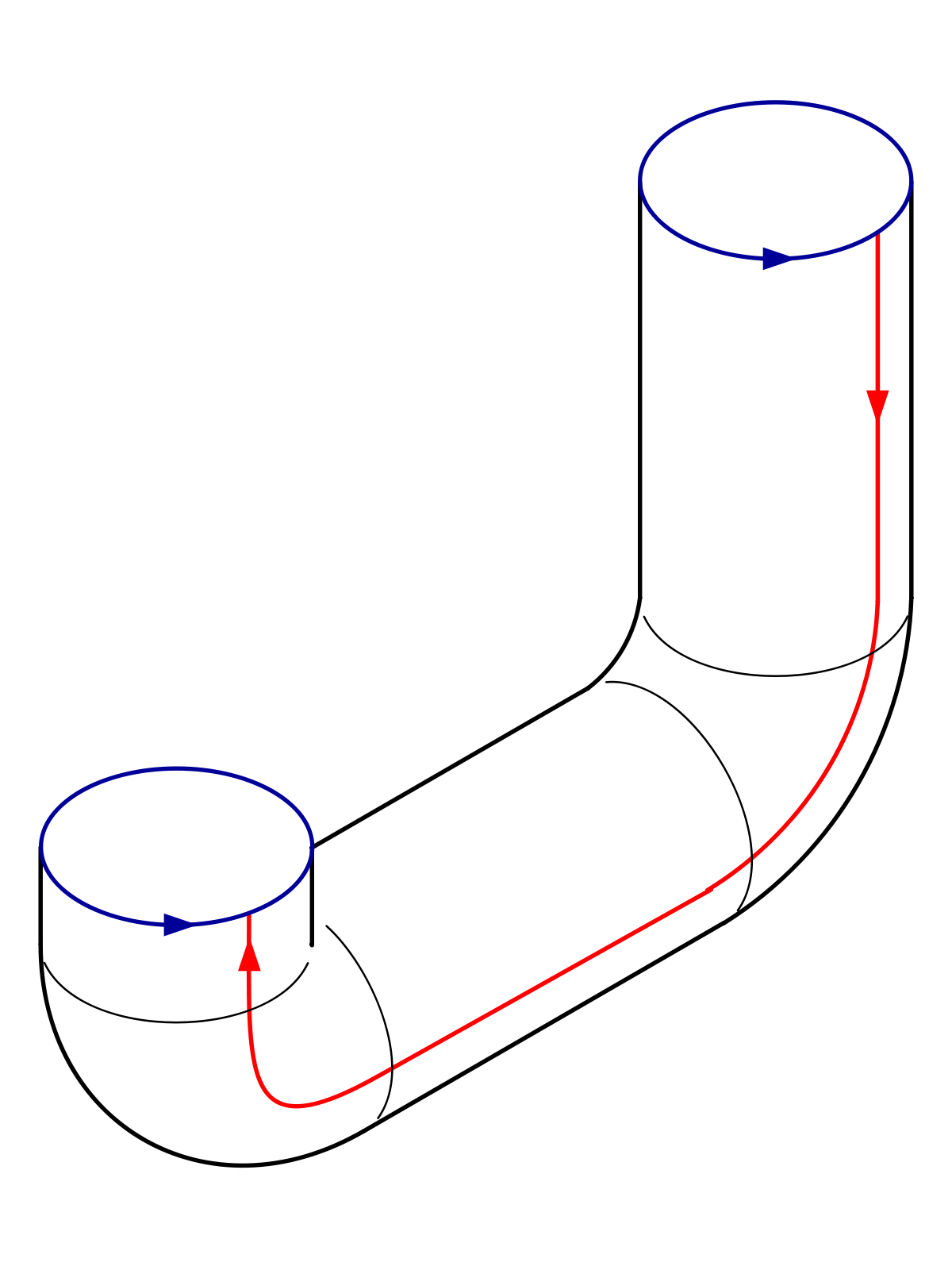
|
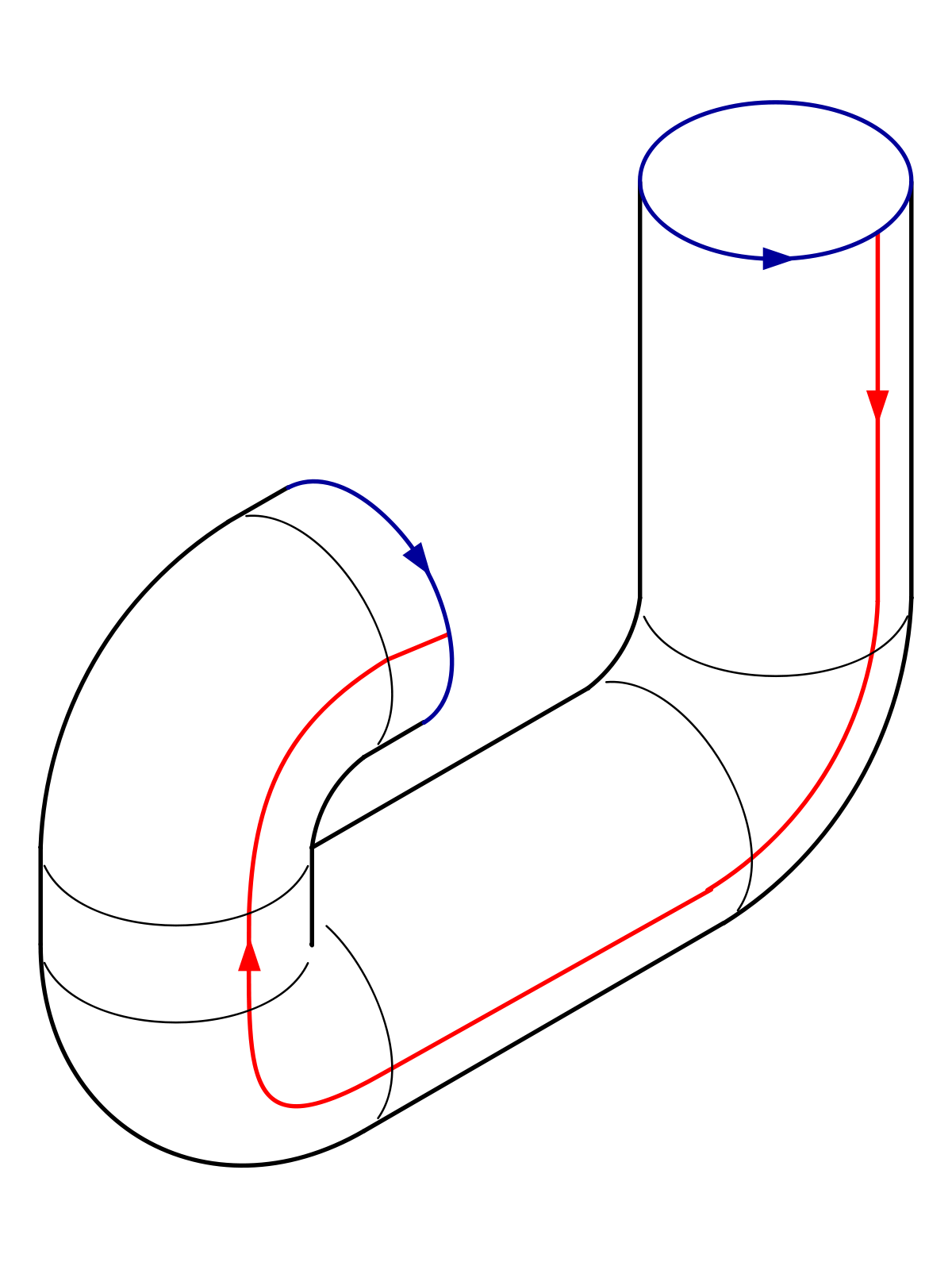
|
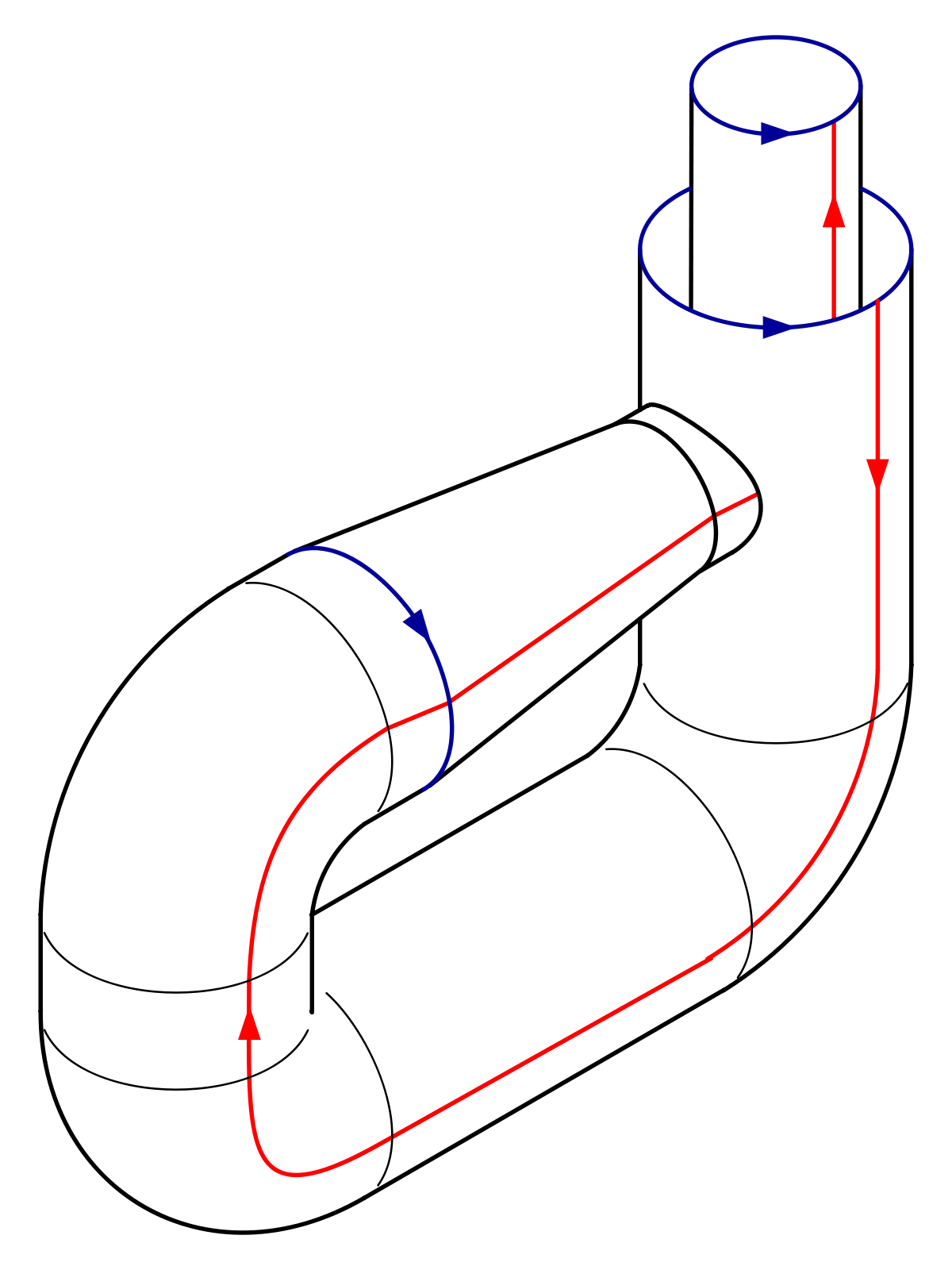
|
|
Construction alternative
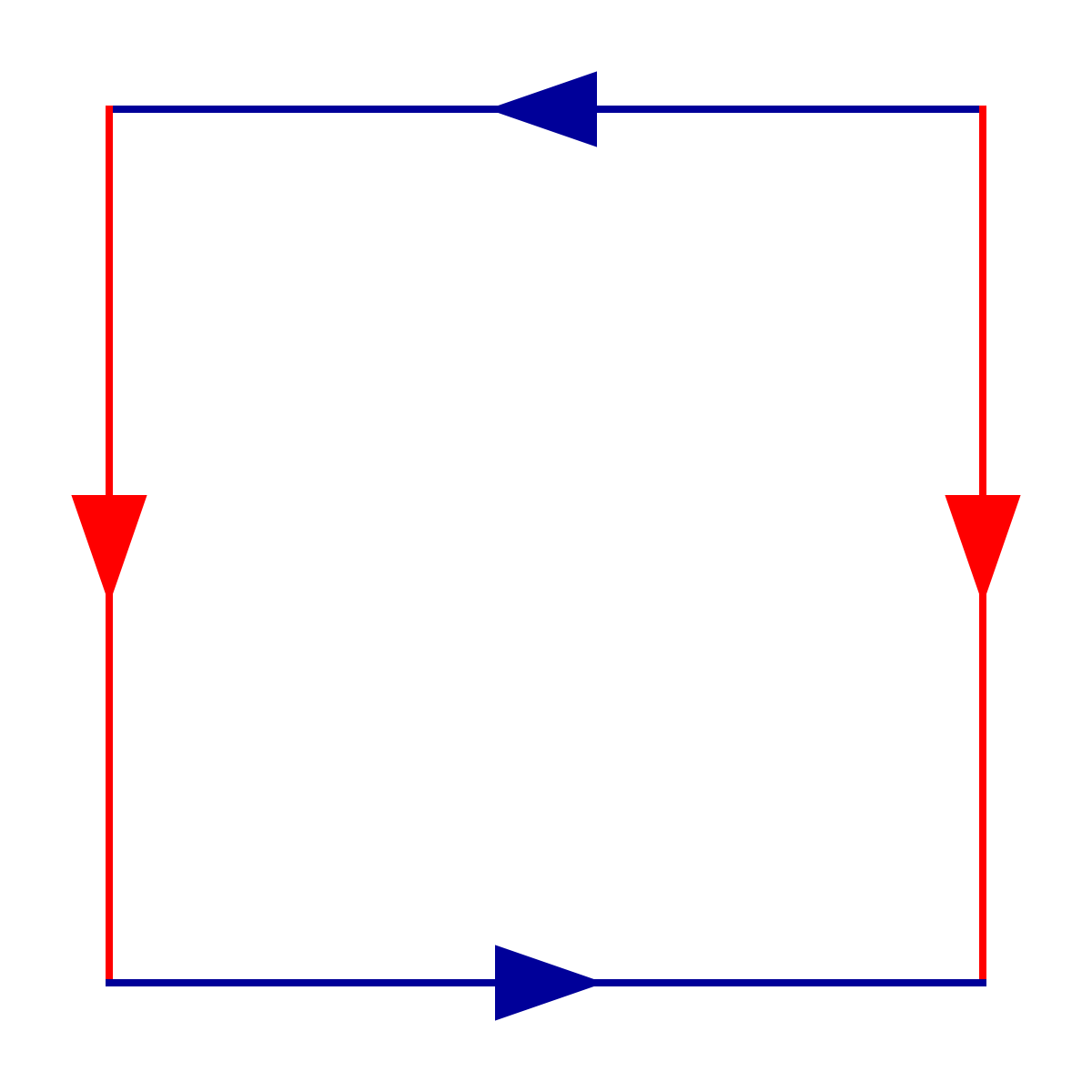
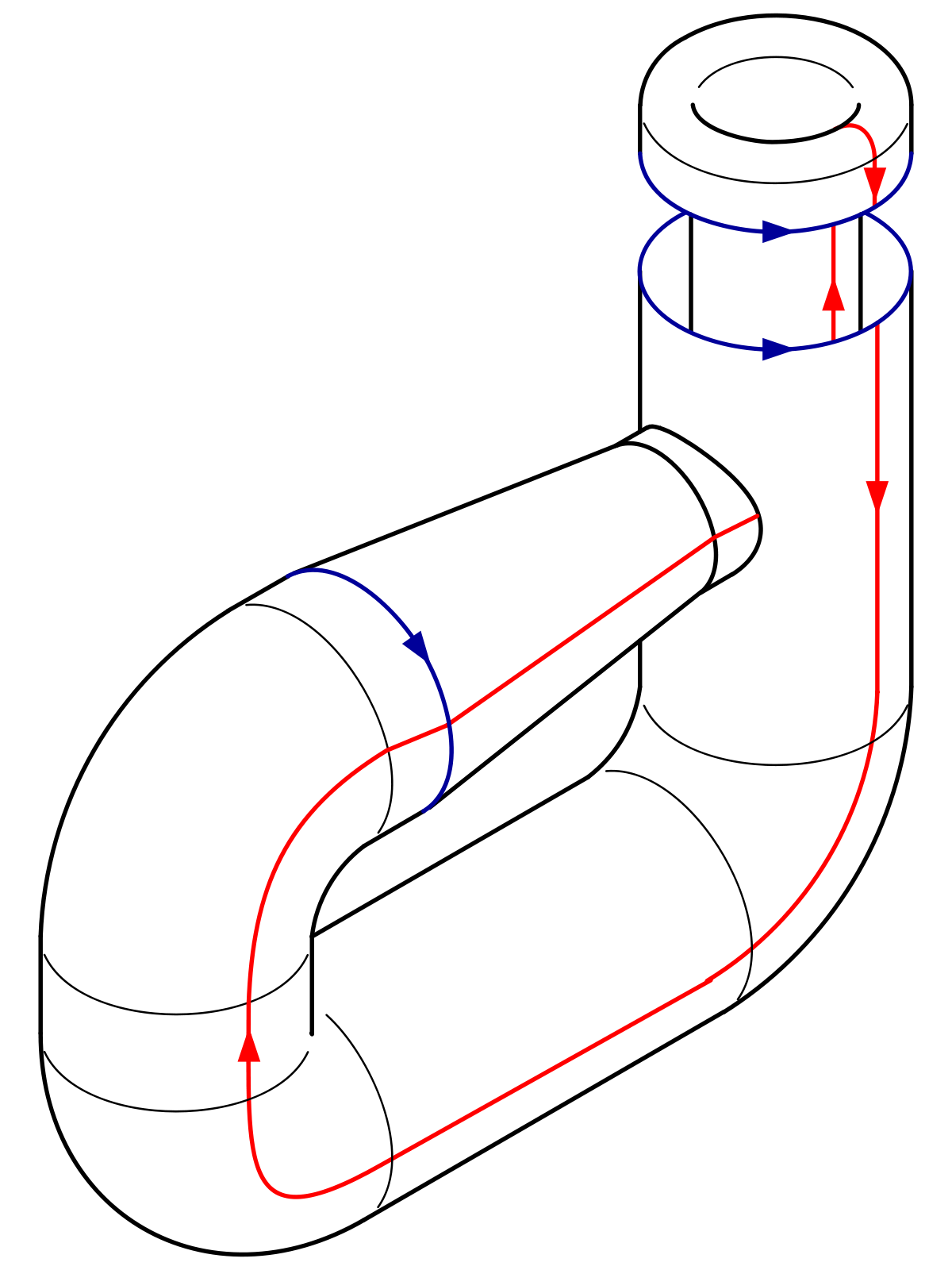
La bouteille de Klein peut aussi être obtenue par recollement de deux anneaux de Möbius le long de leurs bords. On peut imaginer le plan de montage comme suit :

|
On se donne deux exemplaires d'un tel carré, et on obtient deux exemplaires de ruban de Möbius en faisant cette fois d'abord l'identification suivant les flèches bleues. Chacun de ces rubans a alors un seul bord : les côtés verticaux rouges qui ont été connectés suite à l'identification précédente ; recoller les deux rubans suivant leurs bords peut alors être considéré comme équivalent à recoller le bord droit du second carré, au bord gauche du premier, et vice-versa. On voit aisément qu'on retrouve alors bien le cylindre :

|
mais avec l'identification des bords bleus déjà effectuée, c'est-à-dire la bouteille de Klein.
Il est peut-être plus facile de voir qu'une bouteille de Klein coupée en deux dans le sens de la hauteur fournit bien deux rubans de Möbius.
Visualisation

Il est possible de comprendre la structure de la bouteille de Klein à partir de la représentation fournie dans cet article, et au prix d'un effort mental moins important que ce que l'on pourrait croire.
Imaginons un individu vivant dans un monde plat, à 2 dimensions. On essaye alors d'expliquer à l'individu ce qu'est un nœud. Pour cela, on lui dessine un nœud sur le plan : il ne voit qu'une courbe qui s'auto-intersecte. On lui explique alors que ce ne sont pas des points d'intersections qu'il voit, mais que la courbe passe " dessus " et " dessous ". Notre individu est interloqué : vivant dans un monde plat, il ne comprend pas ce qu'est le dessus ni ce qu'est le dessous. Il lui manque une dimension (le haut et le bas) pour pouvoir visualiser le nœud.
Nous rencontrons le même problème lorsque nous essayons de visualiser la bouteille de Klein, puisque nous voyons une surface qui s'auto-intersecte. Néanmoins, si nous raisonnons avec une quatrième dimension, il suffit d'imaginer qu'à cet endroit, la bouteille passe " dessus " et " dessous " au sens de cette quatrième dimension, et donc ne s'auto-intersecte pas.
On peut en quelque sorte considérer que la bouteille de Klein est une surface qui fait un " nœud ". En tant que surface (objet à 2 dimensions), il lui faut 4 dimensions pour faire un nœud, de même que pour une courbe (objet à une dimension) il faut 3 dimensions pour faire un nœud.
Musée du quai Branly
Dans le musée du quai Branly, l'image de la bouteille de Klein est explicitement citée dans un panneau pour expliquer la vision de la sexualité dans les civilisations dites primitives. L'homme parfait est perçu comme un individu dont les parties reproductives se confondent avec l'intérieur de la bouche si bien que cet homme n'a ni intérieur ni extérieur. Pour appuyer le discours, le visiteur peut remarquer la présence de la bouteille de Klein produite en verre comme ci-dessus au milieu de statuettes primitives.
Propriétés
- La bouteille de Klein est la somme connexe de deux espaces projectifs réels.
- En la coupant en deux par rapport à un plan de symétrie, on obtient deux fois un ruban de Möbius.
- Sa caractéristique d'Euler-Poincaré est nulle.
- Ses nombres de Betti non nuls sont b0 = 1 et b1 = 1.
- Son nombre chromatique est 6.
- Sa constante de Powershmit-Gradski vaut
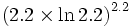
Anecdote
Le nom de la surface, " bouteille de Klein ", provient en fait d'une erreur de traduction de l'expression allemande Kleinsche Fläche (" surface de Klein "). Il y a eu en effet une confusion entre Fläche (" surface ") et Flasche (" bouteille "). Cependant, le terme fautif s'est imposé, y compris en allemand, où l'on utilise maintenant le terme Kleinsche Flasche (" bouteille de Klein "). Il faut dire que l'immersion de la surface de Klein dans
La bouteille de Klein fait l'objet d'un chapitre (XII) dans "la potière jalouse" de Claude Lévi-Strauss (édition Plon 1985): interprétations psychanalitiques et champ sémantique des orifices corporels

















































