Connexité simple - Définition
En topologie, la notion de simple connexité raffine celle de connexité : là où un espace connexe est simplement " d'un seul tenant ", un espace simplement connexe est de plus sans " trou " ni " poignée ".
On formalise cela en disant que tout lacet tracé dans un espace simplement connexe doit pouvoir être réduit continûment (c'est-à-dire par homotopie) à un point.
Définition
Si

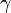

Intuitivement, on peut tirer sur le lacet pour le rétrécir jusqu'à ce qu'il ne forme plus qu'un point, il n'y a pas d'obstacle (c'est-à-dire de trou).
On parle aussi de parties simplement connexes ; une partie d'un espace topologique est dite simplement connexe si, munie de la topologie induite, elle constitue un espace topologique simplement connexe.
Formulations équivalentes :
- On note
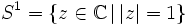
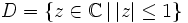

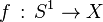
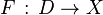
-
- Autrement dit tout plongement d'un cercle dans


- Autrement dit tout plongement d'un cercle dans
- Un espace topologique connexe par arcs est simplement connexe si et seulement si tout couple
![p, \, q : [0,1] \rightarrow X \,\!](https://static.techno-science.net/illustration/Definitions/autres/3/3d66f3a06ad3a5bd58baf0427b19fad6_8180ff433c39731bacb2e4f43e019275.png)

- Un espace topologique connexe par arcs est simplement connexe si et seulement si son groupe fondamental est trivial, c'est-à-dire réduit à l'élément neutre.
Etude d'un cas concret
La droite réelle
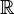
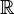
![\gamma \, : \, [0,1] \rightarrow \R \,\!](https://static.techno-science.net/illustration/Definitions/autres/8/833d327c7abcea22678e18fdcca066b0_3f79c0d48051f0f996ea92b551e3f4f7.png)
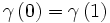
![(\gamma_\alpha )_{\alpha \in [0,1]}\,](https://static.techno-science.net/illustration/Definitions/autres/6/6afd0ef45bb7914fb33d338b249167da_2773196a14084cb5ab0cb562bff116a9.png)
La fonction
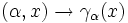
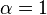
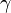
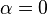
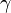
Dans le cas d'un intervalle il suffit de remarquer que:
Et donc tout lacet de la famille est bien définie dans l'intervalle. Nous avons donc démontré que tout lacet simple de
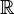
Exemples
Sont simplement connexes :
- le plan complexe
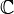
- le disque
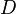
- toute partie convexe ou étoilée d'un espace vectoriel normé ;
- la sphère
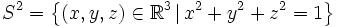
- une assiette, un verre, une fourchette.
Ne sont pas simplement connexes :
-
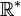
- l'ensemble
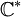
- le cercle
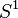
- le tore
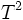
- le ruban de Möbius et la bouteille de Klein ;
- une tasse, une passoire, un fouet de cuisine.
Propriétés
- Théorème : Tout revêtement d'un espace simplement connexe est un revêtement trivial.
- Théorème : Tout revêtement simplement connexe d'un espace est un revêtement universel.
- Propriété de relèvement des homotopies. Toute application f continue d'un espace simplement connexe X dans la base B d'un revêtement
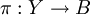
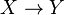
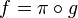
(à compléter)
Généralisations
Espace localement simplement connexes (par arcs)
Un espace est localement simplement connexe tout point admet une base de voisinages simplement connexes. Les espaces localement contractiles sont localement simplement connexes.
Espaces semi-localement simplement connexes (par arcs)
Un espace est dit semi-localement simplement connexe (par arcs) si tout point admet un voisinage U où tout lacet, contenu dans U, peut être déformée en un point dans X.
![\forall \alpha \in [0,1] \quad \forall x \in [0,1] \quad \gamma_\alpha (x) = \gamma(0)+\alpha (\gamma (x)- \gamma (0))\;](https://static.techno-science.net/illustration/Definitions/autres/a/a09783656bbdb431011b81672898b1df_8c7b82d9c29666b63b986e1f3cfdead4.png)
![\forall \alpha \in [0,1] \quad \forall x \in [0,1] \quad \gamma_\alpha (x) \in [\gamma(0),\gamma (x)]\;](https://static.techno-science.net/illustration/Definitions/autres/a/a477e21ae1db893c10fbe8606388caaf_600bcf4f29d4b205eb1b52e49caab376.png)

















































