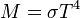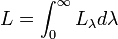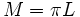Loi de Stefan-Boltzmann - Définition
En physique, la loi de Stefan-Boltzmann[1] établit que la puissance totale rayonnée par unité de surface dans le demi-espace libre du corps noir (exitance[2] énergétique du corps noir) s'exprime par la formule :
où σ est la constante de Stefan-Boltzmann (aussi appelée constante de Stefan).
Loi de Planck
La loi de Stefan se déduit de la loi de Planck, qui permet de déterminer la luminance énergétique totale :
La luminance dans une direction donnée étant par ailleurs pondérée par le cosinus de l'angle par rapport à la normale à la surface émettrice (loi de Lambert), l'exitance énergétique du corps noir est ainsi égale à :
Démonstration
On part de l'expression de la densité spectrale émise par un corps noir (Loi de Planck). On travaille en terme de pulsation. Si u est l'énergie interne par unité de volume (
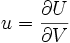
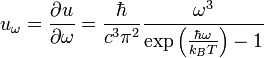
Note : si on veut travailler en longueur d'onde, on peut écrire que
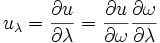
En effet,
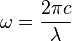
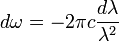
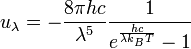
Dans la suite de l'article, on ne travaillera que en pulsation, sachant que tous les calculs peuvent être effectués en utilisant
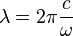
On cherche maintenant à exprimer la puissance surfacique totale (pour toutes les pulsations) émise par un Corps noir. On montre que si
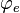
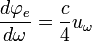
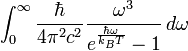
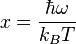
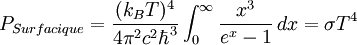
avec
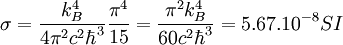
Histoire
La loi de Stefan-Boltzmann a été découverte expérimentalement par Jo?ef Stefan (1835-1893) en 1879, et ses fondations théoriques ont été posées dans le cadre de la thermodynamique par Ludwig Boltzmann (1844-1906), en 1884.
Cette loi est la seule loi physique qui porte le nom d'un physicien slovène.
Stefan publia cette loi le 20 mars dans l'article (allemand) Über die Beziehung zwischen der Wärmestrahlung und der Temperatur (Sur les relations entre radiation thermique et température) dans le Bulletins from the sessions de l'Académie des sciences de Vienne.
Température du Soleil
Grâce à cette loi, Stefan détermina également la température de la surface du Soleil. Il apprend, des données de Charles Soret (1854–1904), que le flux énergétique du Soleil est 29 fois plus grand que celui d'une lamelle de métal chauffée. Soret avait placé une lamelle circulaire devant son appareil de mesure, à une distance telle qu'elle apparaissait sous le même angle que le Soleil. Il avait estimé la température de la lamelle entre 1900 °C et 2000 °C.
Stefan suppose que le tiers du flux énergétique du Soleil est absorbé par l'atmosphère terrestre[3], ainsi il corrige ce rapport du facteur 3/2 : 29 × 3/2 = 43,5. Stefan retient la valeur moyenne des mesures de température de 1950°C, ce qui correspond à une température absolue de 2223 K.
L'application de sa loi conduit à une température du Soleil égale à 43,50,25=2,568 fois la température de la lamelle ; ainsi Stefan obtient une valeur de 5709 K (la valeur est actuellement de 5780 K). Ce fut la première estimation sérieuse de la température du Soleil : les valeurs précédemment avancées variaient entre 1800 °C à 13 000 000 °C.
Rayon des étoiles
Avec la loi de Stefan-Boltzmann, les astronomes peuvent aisément calculer les rayons des étoiles: En effet, la luminosité L d'une étoile s'écrit:
- L = 4πσR2T4
où, L est la luminosité, σ est la constante de Stefan-Boltzmann (ou constante de Stefan), R le rayon de l'étoile, et T sa température. La loi est également respectée dans la thermodynamique des trous noirs pour la radiation de Hawking.
Notes
- ↑ ou de Stefan.
- ↑ Appellation recommandée par la Commission internationale de l'éclairage (anciennement émittance énergétique).
- ↑ La mesure précise de l'absorption atmosphérique ne fut pas réalisée avant 1888 et 1904.