Thermodynamique des trous noirs - Définition

Introduction

La thermodynamique des trous noirs est la branche de l'étude des trous noirs qui s'est développée à la suite de la découverte d'une analogie profonde entre certaines propriétés des trous noirs et les lois de la thermodynamique au début des années 1970. Cette analogie est ensuite devenue pertinente grâce à la découverte par Stephen Hawking du phénomène d'évaporation des trous noirs (1975), démontrant qu'un trou noir n'est pas un objet complètement sombre, mais émet un très faible rayonnement thermique.

L'analogie entre trous noirs et thermodynamique

L'étude des trous noirs indique que ces objets sont décrits par seulement trois paramètres (voir Théorème de calvitie): la masse M, la charge électrique Q et le moment cinétique L. En l'absence de moment cinétique, un trou noir est parfaitement sphérique, mais s'il possède un moment cinétique, il prend une forme légèrement aplatie. Ainsi, le paramètre pertinent décrivant la structure d'un trou noir n'est pas son rayon, mais sa surface (c'est-à-dire la surface de l'horizon des événements qui caractérise le trou noir). Il existe donc une relation liant l'aire d'un trou noir A aux trois paramètres mentionnés.

Il est ainsi possible de calculer de combien varie l'aire d'un trou noir auquel on injecte une petite quantité non nulle soit de matière δM, soit de moment cinétique δL et/ou de charge électrique δQ.

,

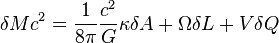
G étant la constante de gravitation, c la vitesse de la lumière, et où les quantités V, Ω et κ s'identifient respectivement au potentiel électrique au voisinage de la surface du trou noir, à sa vitesse angulaire de rotation (déduite de son moment cinétique et de sa masse), et ce que l'on appelle sa gravité de surface, qui mesure à quelle vitesse le champ gravitationnel du trou noir devient infini en son voisinage.

D'après la célèbre formule E=mc², le membre de gauche de cette équation s'identifie à une variation d'énergie. Les termes ΩδL et VδQ s'identifient eux à une variation d'énergie cinétique de rotation et d'énergie potentielle électrique. C'est là une situation extrêmement semblable à ce que l'on retrouve en thermodynamique, où l'on montre qu'une partie de la variation d'énergie interne d'un système est relié au travail des forces extérieure du système. Ainsi, dans la formule bien connue de la thermodynamique,

dU = δQ + δW,

le terme dU ressemble fort au terme δMc² de l'équation des trous noirs, et le terme δW correspond à ΩδL + VδQ quand on considère un système possédant une charge électrique et un moment cinétique. Pour que l'analogie entre trous noir et thermodynamique présente un sens physique, il faut donc supposer que le terme puisse s'identifier au terme δQ qui correspond à la quantité de chaleur fournie au système, selon la formule habituelle reliant celle-ci à la température et à son entropie. Pour cela, il faut entre autres identifier la surface d'un trou noir à une entropie.

Une première étape fut franchie par Stephen Hawking qui démontra que lors de la fusion de deux trous noirs, la surface du trou noir résultant était toujours plus grande que la somme des surfaces des deux trous noirs initiaux. Peu après, en 1974, Hawking mit en évidence le phénomène d'évaporation des trous noirs, où il montra qu'un trou noir rayonnait avec une température proportionnelle à sa gravité de surface. Ainsi, l'identification du terme au terme δQ était-elle complète.