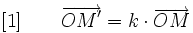Homothétie - Définition
Une homothétie est une transformation géométrique, c'est-à-dire une règle qui associe à chaque point d’un espace un point de ce même espace. On dit aussi que c'est une application mathématique de l'espace sur lui-même.
Le terme, dû au mathématicien français Michel Chasles, est composé des deux éléments d'origine grecque, le préfixe homo- pour " semblable " et thesis pour " position ". Il traduit la correspondance entre deux figures de même forme et de même orientation. Ainsi, deux poupées russes regardant dans la même direction peuvent être vues comme homothétiques.
Dans la suite nous traitons des homothéties du plan, mais les propriétés énoncées restent vraies dans l'espace.
Géométrie du point
Définition
Soient O un point du plan P et k un réel non nul, on appelle homothétie de centre O et de rapport k la transformation qui à tout point M associe le point M' défini par :
Valeurs particulières de k
- pour k = 1
- Chaque point étant invariant, l'homothétie est la transformation identique.
- pour k = -1
- L'homothétie de rapport -1 est la symétrie centrale de centre O.
Propriétés
Propriété vectorielle
Si par l'homothétie h de centre O et de rapport k, A a pour image A ' et B a pour image B ' alors :
-
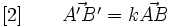
Elle permet de construire l'image de tout point connaissant le centre O de l'homothétie et l'image A' d'un point A.
L'image du point B est le point d'intersection de la droite (OB) et de la droite parallèle à (AB) passant par A'.
Cette égalité caractérise les homothéties : soit f une transformation. On appelle M' l'image de M. S'il existe un réel k, différent de 1, tel que, pour tout point A et tout point B,
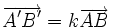
Démonstratin de la propriété 1 : Par l'homothétie h de centre O et de rapport k, h(A)=A', h(B)=B' donc
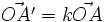
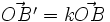
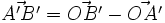
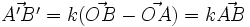
Démonstration de la propriété caractéristique : si f vérifie
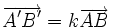
-
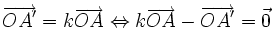
Cette même propriété appliquée alors aux point O et M et à leurs images O et M' donne
-
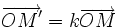
qui est la définition d'un homothétie de cetnre O et de rapport k
Homothétie et trapèze
Si ABCD est un trapèze tel que
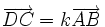

Invariance
- L'homothétie conserve les angles orientés. En particulier elle conserve aussi le parallélisme et l'orthogonalité.
- L'image d'une droite est une droite.
- L'image d'un cercle est un cercle.
- Une homothétie de rapport k,
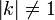
- Si, en général, les homothéties ne conservent pas les distances, elles conservent les proportions. Ce sont donc des similitudes. Comme, de plus, elles conservent les angles orientés, elles font partie des similitudes directes.
Composition
La composée de deux homothéties de centre O et de rapports k et k' est une homothétie de centre O et de rapport kk'. L'ensemble des homothéties de centre O est donc un groupe commutatif isomorphe à R*.
La composée hO' o hO de deux homothéties de centres différents O et O' et de rapports k et k' est
- une translation de vecteur
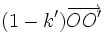
- une homothétie de rapport kk' et de centre O" barycentre des points (O , kk'- k') et (O' , k'-1) si kk' est différent de 1.
La composée t o h d'une homothétie de centre O et de rapport k et d'une translation de vecteur

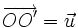
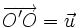
Ces propriétés font de l'ensemble des homothéties-translations est un groupe non commutatif.
Géométrie vectorielle
Dans un espace vectoriel V sur un corps K, on appelle homothétie de rapport k (k non nul) , l'application qui, à tout vecteur


C'est un cas particulier d'application linéaire. Dans une homothétie, il n'existe qu'une seule valeur propre : k et tous les vecteurs sont des vecteurs propres. La matrice d'une homothétie dans un espace vectoriel de dimension n est k*In où In est la matrice Identité.