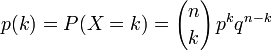Loi binomiale - Définition
En mathématiques, une loi binomiale de paramètres n et p correspond au modèle suivant :
On renouvelle n fois de manière indépendante une épreuve de Bernoulli de paramètre p (expérience aléatoire à deux issues possibles, généralement dénommées respectivement " succès " et " échec ", la probabilité d'un succès étant p, celle d'un échec étant q = 1 − p). On compte alors le nombre de succès obtenus à l'issue des n épreuves et on appelle X la variable aléatoire correspondant à ce nombre de succès.
L'univers
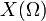
La variable aléatoire suit une loi de probabilité définie par :
En France, le premier terme du membre de droite est noté
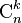
Les symboles
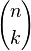
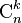
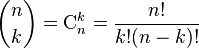
Cette loi de probabilité s'appelle la loi binomiale de paramètre (n ; p) et se note B(n ; p).
Calcul de p(k)
Une épreuve de Bernoulli conduit à la création d'un univers Ω = {S ; E}.
n épreuves de Bernoulli indépendantes conduisent à la création d'un univers Ωn constitué de n-uplets d'éléments de Ω, sur lequel peut se définir une probabilité produit. La probabilité de l'éventualité (S, S, ..., S, E, E, ..., E) avec k succès et n - k échecs a donc pour valeur pkqn-k.
Plus généralement, tout n-uplet formé de k succès et de n-k échecs aura pour probabilité pkqn-k quel que soit l'ordre d'apparition des S et des E.
L'évènement " X = k " est formé de tous les n-uplets comportant k succès et n - k échecs. La combinatoire permet de déterminer le nombre de n-uplets de ce type : il y en a autant que de parties à k éléments d'un ensemble à n éléments ; or chaque partie correspond à une façon de placer les k succès parmi les n places du n-uplet. Il y a donc
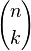
Donc
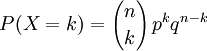
Espérance, variance, écart type
X est la somme de n variables aléatoires indépendantes suivant toutes la (même) loi de Bernoulli de paramètre p, prenant la valeur 1 en cas de succès (probabilité p) et 0 en cas d'échec (probabilité (1-p)) ; ces variables aléatoires ont pour espérance p et pour variance p(1-p).
- E(X) est donc la somme des espérances, soit np
- V(X) est la somme des variances, soit np(1-p)
-
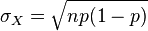
Convergence
Pour de grandes valeurs de n, le calcul de
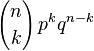
- Lorsque n tend vers l'infini et que p tend vers 0 avec np = a, la loi binomiale converge vers une loi de Poisson de paramètre a. En pratique, on remplace la loi binomiale par une loi de Poisson dès que n > 30 et np < 5.
- Lorsque n tend vers l'infini et que p et q sont de même ordre de grandeur, la loi binomiale converge vers une loi normale d'espérance np et de variance npq. En pratique, on remplace une loi binomiale par une loi normale dès que n > 30, np > 5 et nq > 5
Supposons que p(k) admette un extremum pour
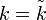
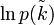
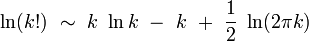
Il vient :
![\ln p(k) \ \sim \ n \ \ln n \ - \ n \ + \ \frac{1}{2} \ \ln ( 2 \pi n) \ - \ \left[ \ k \ \ln k \ - \ k \ + \ \frac{1}{2} \ \ln ( 2 \pi k) \ \right]](https://static.techno-science.net/illustration/Definitions/autres/9/947c75fb3fc52ebe75676aab0ef2ce81_a1d56d1b15654eb4a4046deb22b3242c.png)
![\ - \ \left[ \ (n-k) \ \ln (n-k) \ - \ (n-k) \ + \ \frac{1}{2} \ \ln ( 2 \pi (n-k) \, ) \, \right] \ + \ k \ln p \ - \ (n-k) \ln (1-p)](https://static.techno-science.net/illustration/Definitions/autres/e/edad49e47e13c7dc60017381401422b3_e8ae1e0290cc2b1e4469f5f92381f36c.png)
La dérivée par rapport à k donne :
![\frac{d~}{dk} \ln p(k) \ \sim \ \ln \left[ \, \frac{(n-k) \ p}{k \ (1 - p)} \, \right] \ + \ O \left( \frac{1}{k} \right)](https://static.techno-science.net/illustration/Definitions/autres/6/654ed8bcdeb5544d4f033529dc1ea92a_16dac8de587ceeb8d7e2761440bd9ec5.png)
Pour annuler cette dérivée, il faut que l'argument du logarithme soit égale à un. On obtient alors la valeur de k qui rend le logarithme extremum :
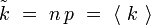
La valeur la plus probable est donc la valeur moyenne. La dérivée seconde vaut par ailleurs :
![\frac{d^2~}{dk^2} \ln p(k) \ \sim \ - \ \left[ \, \frac{1}{n-k} \ + \ \frac{1}{k} \, \right] \ + \ O \left( \frac{1}{k^2} \right)](https://static.techno-science.net/illustration/Definitions/autres/e/e00678b5c870f04ecc2697d6e35730c4_9607ed463cd75366bd2e0ec95fa1949b.png)
Calculée en
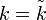
![\frac{d^2~}{dk^2} \ln p(\tilde{k}) \ \sim \ - \ \left[ \, \frac{1}{np(1-p)} \, \right] \ = \ - \ \frac{1}{\sigma^2}](https://static.techno-science.net/illustration/Definitions/autres/d/d219dc5afa044a884df04dea3bf2add8_2304bb2d4cc462314c3d47f295735677.png)
On peut donc écrire le développement limité au second ordre suivant :
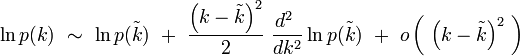
qui s'écrit compte-tenu de ce qui précède :
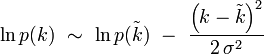
soit en prenant l'exponentielle :
![p(k) \ \sim \ p(\tilde{k}) \ \exp \ \left[ - \ \frac{\left( k - \tilde{k} \right)^2}{2 \, \sigma^2} \ \right]](https://static.techno-science.net/illustration/Definitions/autres/d/d2d4b67d617bc558f50c4e8cfefa8c03_0ddb1130f006a81cb1c4d0fa47f2a9f0.png)
On détermine la constante
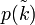
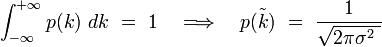
d'où la distribution gaussienne :
![p(k) \ = \ \frac{1}{\sqrt{2 \pi \sigma^2 \ }} \ \exp \ \left[ - \ \frac{\left( k - \langle \ k \ \rangle \, \right)^2}{2 \, \sigma^2} \ \right]](https://static.techno-science.net/illustration/Definitions/autres/a/af25d49973129a7512ec90450721f597_959a5b1350378a57098b5dac6e328f5e.png)
Loi des grands nombres
La loi binomiale, son espérance et sa variance, ainsi que l'inégalité de Bienaymé-Tchebychev permettent de démontrer une version simple de la loi des grands nombres.