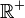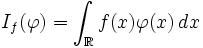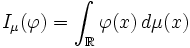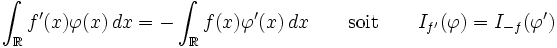Distribution (analyse mathématique) - Définition
En analyse mathématique, une distribution (également appelée fonction généralisée) est un objet qui généralise la notion de fonction et de mesure. La théorie des distributions étend la notion de dérivée à toutes les fonctions localement intégrables et au-delà, et est utilisée pour formuler des solutions à certaines équations aux dérivées partielles. Elles sont importantes en physique et en ingénierie où beaucoup de problèmes discontinus conduisent naturellement à des équations différentielles dont les solutions sont des distributions plutôt que des fonctions ordinaires.
La théorie des distributions fut formalisée par le mathématicien français Laurent Schwartz et lui valut la médaille Fields en 1950. Son introduction utilise des notions d'algèbre linéaire et de topologie centrées autour de l'idée de dualité.
La distribution de Dirac est un exemple intéressant de distribution car elle n'est pas une fonction au sens strict du terme, mais peut être représentée de façon informelle par une fonction dégénérée qui serait nulle sur tout son domaine de définition sauf en 0 et dont l'intégrale vaudrait 1. Un tel objet mathématique est utile en physique ou bien en traitement du signal mais aucune fonction ordinaire n'a ces propriétés.
Idée de base
On évalue habituellement une fonction en calculant sa valeur en un point. Toutefois cette méthode fait jouer un rôle considérable aux irrégularités (discontinuités par exemple) de la fonction. L'idée sous-jacente à la théorie des distributions est qu'il existe un meilleur procédé d'évaluation : calculer une moyenne des valeurs de la fonction dans un domaine de plus en plus resserré autour du point d'étude. En envisageant des moyennes pondérées, on est donc conduit à examiner des expressions de la forme
dans laquelle la fonction à évaluer
L'intégrale


D'une manière plus générale, si μ est une mesure sur les réels et

est un nombre réel qui dépend de façon linéaire et continue de

Les distributions peuvent être multipliées par un nombre réel quelconque et additionnées entre elles. L'ensemble des distributions forme ainsi un espace vectoriel réel. Il n'est pas possible de définir en général le produit de deux distributions en tant que généralisation du produit ponctuel de deux fonctions, mais les distributions peuvent être multipliées par des fonctions indéfiniment dérivables.
Théorie des distributions
Espace des fonctions test
Soit Ω un espace topologique. L'espace des fonctions test
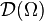
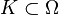
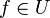
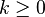
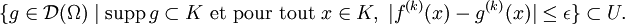
Muni de cette topologie,
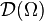
Exemple de fonction test :
Pour
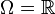
La fonction


![[-1,1]\,](https://static.techno-science.net/illustration/Definitions/autres/5/581a26dec23e9f937a02a278e20fc9c3_1bd6d8bf4f5c00e5b9985cbab7076182.png)
Distributions
Définition
Une distribution est une forme linéaire continue sur
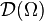
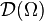
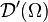
Notation
Si T est une distribution et

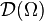
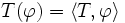
Exemple
Dans


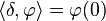
Dérivation des distributions
Pour définir la dérivée d'une distribution, voyons d'abord le cas d'une fonction différentiable et intégrable

Comme la fonction

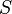
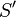

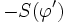
Par exemple la dérivée au sens des distributions de la fonction caractéristique de