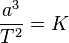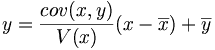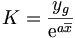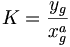Série statistique à deux variables - Définition
Cet article fait partie de la série Mathématiques élémentaires |
| Algèbre |
| Analyse |
| Arithmétique |
| Géométrie |
| Logique |
| Probabilité |
| Statistique |
Il arrive fréquemment que l'on observe conjointement deux caractères statistiques pour déterminer s'il existe une corrélation entre les deux (âge et taille des enfants entre 0 et 20 ans, prix du m² et année, allongement du ressort et force appliquée, etc.)
Traitement des données
Pour chaque individu, on relève la valeur de deux caractères x et y. On obtient alors une liste de couples de nombres (xi;yi) que l'on peut présenter sous forme d'un tableau.
Exemple 1: moyenne de l'année et note à l'examen pour un échantillon de 24 personnes .
| Note de l'année | 8 | 9 | 7 | 15 | 12 | 12 | 10 | 8 |
| Note à l'examen | 7 | 9 | 4 | 17 | 13 | 15 | 9 | 13 |
| Note de l'année | 11 | 11 | 7 | 8 | 11 | 11 | 12 | 12 |
| Note à l'examen | 14 | 9 | 11 | 10 | 9 | 12 | 17 | 12 |
| Note de l'année | 7 | 9 | 9 | 5 | 9 | 5 | 10 | 4 |
| Note à l'examen | 8 | 15 | 12 | 7 | 14 | 12 | 11 | 7 |
Exemple 2: Masse appliquée (en gramme) et longueur du ressort (en cm).
| Masse en grammes | 7 | 10 | 18 | 20 | 5 | 24 | 12 | 3 |
| Longueur en cm | 8.5 | 9 | 10.5 | 11 | 8 | 11.8 | 9.4 | 7.5 |
Caractéristiques numériques
On peut étudier séparément chaque caractère statistique et calculer leur moyenne
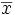

On aura besoin de définir des quantités qui font intervenir conjointement les deux caractères:
- la covariance cov(x,y) =
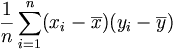
- le coefficient de corrélation linéaire r =
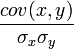
Représentation graphique
Chaque couple de réels (xi,yi) définit un point Mi de coordonnées (xi,yi). L'ensemble de ces points s'appelle un nuage de points. Il arrive que deux points aient les mêmes coordonnées, ils seront alors représentés par un point dont la surface sera deux fois celle des autres.
On peut aussi placer le point moyen. C'est le point G dont les coordonnées sont

Le nuage de points est un bon indicateur pour vérifier une corrélation entre les caractères x et y. Si les points sont sous la forme d'un nuage, il est fort à parier que les phénomènes ne sont pas corrélés. S'ils semblent dessiner une courbe, on cherchera à déterminer la nature de la courbe en procédant à un ajustement.
Exemple 1: Nuage de points donnant la note à l'examen en fonction de la moyenne de l'année.

L'observation du nuage de points laisse supposer qu'il n'existe pas de corrélation nette entre les notes de l'année et les notes à l'examen. Le calcul du coefficient de corrélation donne pour résultat 0,6 trop faible pour conclure à une corrélation. On peut toutefois observer qu'une grande partie du nuage est situé au-dessus de la droite d'équation y = x ce qui laisse penser que les élèves se sont mieux sortis de l'examen que du contrôle continu.
Exemple 2: Nuage de points donnant la longueur du ressort en fonction de la masse appliquée.

Les points semblent alignés. On va donc tenter un ajustement affine.
Ajustement
Ajustement affine
Si les points semblent alignés, on détermine la droite d'ajustement grâce à une régression linéaire.
La droite d'ajustement a pour équation:
Elle passe par le point moyen G.
Cet ajustement est considéré comme valide si le coefficient de corrélation linéaire r est en valeur absolue supérieur à

Exemple du ressort
La droite de régression a pour équation y = 0,2x + 7 et le coefficient de corrélation est pratiquement égal à 1. On peut donc affirmer sans trop d'erreur que l'allongement du ressort est proportionnel à la masse appliquée (lois de déformation élastique). Le fait que les points ne soient pas exactement alignés provient des erreurs ou imprécisions des mesures.

Ajustement exponentiel
Si les points semblent dessiner une exponentielle, il n'est pas adéquat de tenter un ajustement affine. Pour vérifier la corrélation exponentielle, il est bon de tracer un nouveau nuage de point de coordonnées (xi,zi = ln(yi)), ou bien de tracer le nuage de points dans un repère semi-logarithmique. Si les points semblent alignés, on peut tenter un ajustement affine de zi en fonction de xi.
Si la droite d'ajustement a pour équation z = ax + b, cela signifie que ln(y) = ax+b. Il existe donc une relation exponentielle entre y et x:
Les formules de régression linéaire donnent
- pour a.
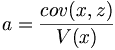
- pour K.
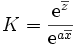
Et si on appelle yg, la moyenne géométrique des yi, on remarque que
La courbe passe alors par le point

Exemple 3: Evolution de l'actif net d'une mutuelle de 1988 à 1997 (d'après bac Nouvelle Calédonie décembre 2000).
| année depuis 1900 : xi | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 |
| Actif net en milliards d'Euros: yi | 5,89 | 6,77 | 7,87 | 9,11 | 10,56 | 12,27 | 13,92 | 15,72 | 17,91 | 22,13 |
| zi = ln(yi) | 1,7733 | 1,9125 | 2,0631 | 2,2094 | 2,358 | 2,5072 | 2,6333 | 2,7549 | 2,8854 | 3,0969 |
Le tracé du nuage de points montre plutôt le dessin d'une fonction exponentielle. Le soupçon est confirmé par le tracé du nuage de points de coordonnées (xi;zi) qui donne des points presque alignés.
L'ajustement affine de z en fonction de x conduit à l'équation z = 0,143x - 10,813 avec un coefficient de corrélation voisin de 1.
On peut donc affirmer que l'évolution de l'actif semble être une fonction exponentielle de l'année:
- y = e0,143x − 10,813

Tracé du nuage et de l'ajustement exponentiel
Ajustement sous forme de puissance
Il est possible aussi que la relation soit sous forme de puissance. Le phénomène est difficile à voir sur le nuage de point. Si on soupçonne une corrélation du type puissance, on trace le nuage des points de coordonnées (ti = ln(xi),zi = ln(yi)), ou bien on trace le nuage de points de coordonnées (xi,yi) dans un repère log-log. Si les points paraissent alignés on tente une régression linéaire de zi en fonction de ti.
Si la droite d'ajustement a pour équation z = at + b, cela signifie que ln(y) = aln(x)+b. Il existe donc une relation en puissance entre y et x:
Les formules de régression linéaire donnent
- pour a.
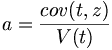
- pour K.
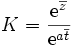
Et si on appelle yg, la moyenne géométrique des yi et xg, la moyenne géométrique des xi on remarque que
La courbe passe alors par le point Mg(xg,yg)
Exemple: Étude de la période de certaines planètes en fonction du demi-grand axe de leur trajectoire.
| Planète | demi grand axe a en 109 m | période T en 106s | ln(a) | ln(T) |
| Mercure | 57,9 | 7,59 | 4,059 | 2,025 |
| Venus | 108,2 | 19,36 | 4,684 | 2,863 |
| Terre | 149,6 | 31,47 | 5,008 | 3,449 |
| Mars | 227,9 | 59,19 | 5,429 | 4,081 |
| Jupiter | 778,3 | 373,32 | 6,657 | 5,992 |
Une représentation du nuage de points dans un repère log-log présente des points presque alignés.
Un ajustement linéaire de ln(T) en fonction de ln(a) conduit à l'équation :
- ln(T) = 1,5ln(a) - 4,062
avec un coefficient de corrélation linéaire très proche de 1.
Ce qui conduit à la relation suivante:
-
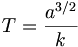
-