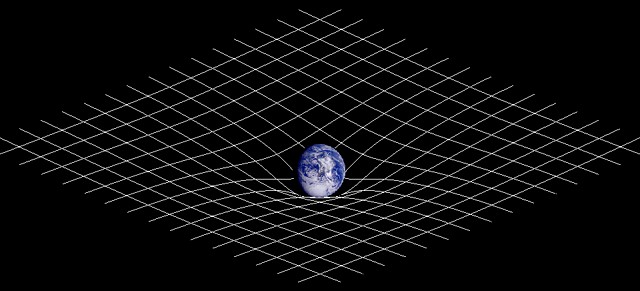
La relativité: principes fondamentaux
Publié par Publication le 20/09/2009 à 14:04
Pouvant inclure des liens partenaires
Pouvant inclure des liens partenaires
303
La Relativité
1 - Introduction
Ce dossier nous est proposé par Bongo1981, que vous pouvez retrouver sur le forum Techno-Science.net. Il présente les bases et les principes de la Relativité.
Lorsque nous parlons de physique moderne, de scientifiques, de génies, tout le monde évoque Albert Einstein. Quand nous questionnons les gens sur les travaux d'Einstein, tout le monde répond en coeur: E=mc², la théorie de la relativité, la bombe atomique.
Mais au fait ? Que veulent dire tous ces termes ? Pourquoi Einstein est-il considéré comme l'un des plus grands physiciens de tous les temps ? Nous allons tenter dans ce dossier de présenter le principe de relativité, ses conséquences profondes sur les théories de la physique classique, les limites de la physique classique, et les observations qui ont conduit Einstein, guidé par son sens physique, son intuition déconcertante, à bouleverser nos concepts de l'espace et du temps pour révolutionner toute la physique bien établie de la fin du XIX ème siècle, qui sont la cinématique, la dynamique, ainsi que la théorie de la gravitation de Newton, si solidement confirmées par l'expérience, et si profondément ancrées dans nos intuitions de tous les jours.
Certaines parties seront assez techniques, mais rassurez-vous, aucune connaissance préalable n'est requise, et les conclusions sont toujours rappelées pour interpréter les équations.
Introduction
Lorsque nous parlons de physique moderne, de scientifiques, de génies, tout le monde évoque Albert Einstein. Quand nous questionnons les gens sur les travaux d'Einstein, tout le monde répond en coeur: E=mc², la théorie de la relativité, la bombe atomique.
Mais au fait ? Que veulent dire tous ces termes ? Pourquoi Einstein est-il considéré comme l'un des plus grands physiciens de tous les temps ? Nous allons tenter dans ce dossier de présenter le principe de relativité, ses conséquences profondes sur les théories de la physique classique, les limites de la physique classique, et les observations qui ont conduit Einstein, guidé par son sens physique, son intuition déconcertante, à bouleverser nos concepts de l'espace et du temps pour révolutionner toute la physique bien établie de la fin du XIX ème siècle, qui sont la cinématique, la dynamique, ainsi que la théorie de la gravitation de Newton, si solidement confirmées par l'expérience, et si profondément ancrées dans nos intuitions de tous les jours.
Certaines parties seront assez techniques, mais rassurez-vous, aucune connaissance préalable n'est requise, et les conclusions sont toujours rappelées pour interpréter les équations.
2 - Relativité Galiléenne

Galiléo Galiléi 1564-1642
Dans cette partie nous allons appréhender le principe de relativité par des exemples de la vie courante. Le principe de relativité a été formalisé par Galilée en 1632 (ou Galiléo Galiléi 1564 - 1642), physicien italien. C'est seulement à partir de ce moment, que la physique s'est séparée de la philosophie, et est devenue une discipline, à part entière, à caractère expérimental, comme nous la connaissons aujourd'hui.
Principe
Le principe de relativité affirme que les lois de la physique restent identiques dans tout référentiel galiléen.
Définition et exemples de référentiels
Tout d'abord qu'est-ce qu'un référentiel ? C'est une référence (souvent attachée à un corps, imaginaire ou existant) par rapport à laquelle l'on décrit un phénomène. En effet, pour observer un phénomène, il faut un observateur, qui est lui-même attaché à un référentiel.Par exemple nous pouvons observer le mouvement de la valve d'une bicylette:
- par rapport au cycliste, la trajectoire est un cercle
- par rapport à la terre ferme, la trajectoire est courbe (des sortes de grands arcs de cercle qui ne reviennent pas en arrière, que les mathématiciens appellent cycloïdes)
Référentiel Galiléen
Un référentiel galiléen est un référentiel où lorsqu'aucune force n'est appliquée à un mobile, celui-ci est soit au repos soit en translation rectiligne uniforme, ce qui veut dire que le mobile se déplace en ligne droite à vitesse constante.Exemple de la vie courante

© Alstom
Qui a déjà voyagé en train, et s'est déjà demandé, lorsque le train arrive en gare, ou part de la gare, et croise un autre train, à vitesse constante, dans la nuit, sans référence extérieure, si c'était son propre train qui était au repos, ou bien l'autre train ?
Puisque le train voyage en ligne droite, et à vitesse constante, nous ne ressentons rien, seulement notre corps appuyé vers le bas contre le siège.
Il est naturellement plus facile de marcher dans le train, lorsque celui-ci est en ligne droite, à vitesse constante, à 450 km/h par rapport au sol, que lorsque le train effectue un virage, ou effectue un freinage appuyé.
Ceci veut dire qu'il est impossible de savoir si l'on est en mouvement ou non par n'importe quelle expérience physique. En d'autres termes, il n'y a pas d'état de repos absolu.
Mécanique classique
Nous constatons tous les jours que la nature respecte le principe de relativité, c'est pourquoi les lois écrites par les physiciens doivent respecter ce principe. Cela se traduit mathématiquement par certaines contraintes.
Par exemple lorsque l'on observe un phénomène physique dans le référentiel R, par exemple les paramètres telles que la masse m, l'accélération a, et la force F, nous savons depuis Newton que cette relation est vérifiée:
F = m a
Dans le référentiel R' nous observerons les mêmes paramètres, avec des valeurs primées: m', a', et F'. Dans le référentiel R' nous devons avoir:
F' = m' a'
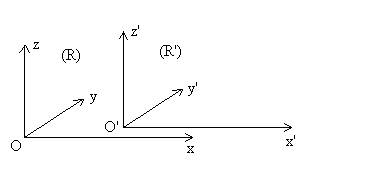
Référentiels en translation rectiligne uniforme
Le principe de relativité se traduit par des transformations mathématiques des coordonnées:
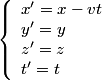
Ceci traduit deux référentiels en mouvement rectiligne uniforme (v est une constante) dans la direction Ox. Ces transformations permettent de connaître les coordonnées d'un mobile dans un référentiel R, connaissant ses coordonnées dans le référentiel R' par exemple.
Pour la formulation mathématique, nous savons que la masse reste invariante quand on change de référentiel: m=m', ainsi que la force F=F'.
En dérivant 2 fois par rapport au temps l'expression de x', nous obtenons: d²x'/dt² = d²x/dt² (l'on obtient bien a'=a).
Problèmes

James Clerk Maxwell 1831 - 1879
Les équations de Maxwell, formulées en 1864, décrivent les lois de l'électromagnétisme. Ces lois prédisent l'existence d'ondes électromagnétiques voyageant à la vitesse c. Or nous voyons tout de suite le problème: les ondes électromagnétiques se propagent à la célérité c, mais par rapport à quoi donc ? Dans quel référentiel doit-on mesurer cette vitesse précise ? La théorie ne le précise pas.
Les physiciens ont supposé qu'il existait une substance remplissant tout l'espace: l'éther, ayant des propriétés étranges. Ils se sont proposés de mettre en évidence cette substance, en démontrant qu'il existe un vent d'éther, puisque la terre se déplace dans l'espace, et donc l'éther représenterait le repos absolu, contredisant le principe de relativité de Galilée.
Description de l'expérience de Michelson Morley
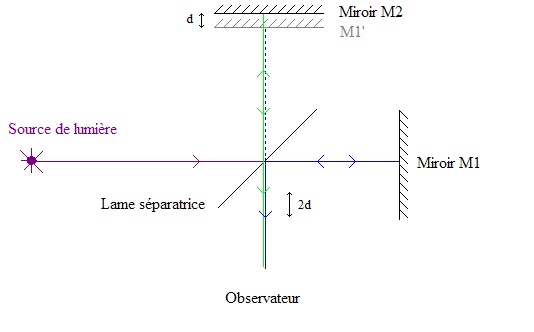
Expérience de Michelson Morley 1887
L'expérience de Michelson Morley exploite la nature ondulatoire de la lumière. En effet, celui-ci est formé de deux bras orthogonaux l'un par rapport à l'autre. Au milieu se situe une lame semi réfléchissante séparant un faisceau de lumière émis par la source, celui-ci se divise en deux, parcourant les deux bras deux fois (une fois en sens aller, se réfléchissant sur le miroir situé aux extrémités des deux bras et une fois en sens retour, puis les deux faisceaux se reconvergent à nouveau sur un écran). Nous pouvons régler la longueur des bras grâce à des vis micrométriques, permettant de former une figure d'interférence.
Nous pouvons régler la longueur des bras afin que le chemin optique soit strictement identique (qui est un tout petit peu différent de la longueur des bras), obtenant les teintes de Newton.
Nous voulons mettre en évidence le mouvement de la terre dans l'éther, c'est pourquoi l'interféromètre réglé convenablement 6 mois auparavant ne doit plus être réglé correctement 6 mois après puisque la terre a une vitesse différente (elle est de l'autre côté du soleil).
Résultat négatif de l'expérience
L'expérience de Michelson-Morley a démontré qu'il n'existait pas de vent d'éther, alors les physiciens ont échafaudé d'autres théories, comme quoi l'éther était partiellement entraîné par la terre, (mais vite contredite par l'aberration de la lumière), ou que dans le mouvement par rapport à l'éther, les longueurs et le temps étaient affectés... (contraction et dilatation de Lorentz).L'arrivée d'un inconnu: Einstein

Albert Einstein 1879 - 1955
La solution fut apportée par un illustre inconnu, un ingénieur de 3ème catégorie du bureau des brevets de Berne: Albert Einstein. Selon ses professeurs (Hermann Minkowski par exemple, qui jouera un rôle important dans le formalisme de la relativité restreinte), c'était un chien fainéant, et il n'arriverait à rien dans la vie.
3 - Relativité Restreinte
Conséquences sur la mécanique classique, et l'Espace-temps
Indépendance de la célérité de la lumière par rapport à n'importe quel référentiel
Selon Einstein, les équations de Maxwell ne précisent pas par rapport à quel référentiel les ondes électromagnétiques se propagent, tout simplement par ce qu'il n'y a pas besoin de le préciser, les ondes électromagnétiques se propagent à la célérité c par rapport à n'importe quel référentiel. Ceci est totalement contre intuitif, et stupéfiant.En effet, dans la vie de tous les jours, lorsque quelqu'un marche à 5km/h sur un tapis roulant à 3km/h, et dans le même sens, tout le monde s'attend à le voir à 8km/h par rapport au sol. Donc pour la lumière, qui a une célérité dans le vide de 300 000 km/s, si celle-ci est transportée par un avion volant vers nous à 1km/s (ça fait tout de même un avion très rapide, de l'ordre de mach 3, le Blackbird SR-71 devrait faire l'affaire), nous nous attendrions à voir la lumière un peu plus rapide: 300 001 km/s (mais ce n'est pas le cas, la vitesse de la lumière reste la même).
Postulats de la Relativité Restreinte
Einstein sait que cela va à l'encontre de toute la mécanique classique, qui a connu énormément de succès expérimentaux depuis 300 ans, depuis les travaux de l'illustre Sir Isaac Newton. Par ailleurs avec cette assertion, Einstein sait qu'il bouleverse nos conceptions d'espace et de temps.Selon Einstein, dans son article éblouissant de 1905, modestement intitulé "Sur l'électrodynamique des corps en mouvement", le principe de relativité restreinte est basé sur deux postulats:
- les lois de la physique sont les mêmes dans tous les référentiels galiléens
- la vitesse de la lumière est la même dans tous les référentiels.
Les transformations de Lorentz
Cela aboutit aux transformations de Lorentz, qui permettent de passer d'un référentiel galiléen à un autre, ces transformations remplacent les transformations de Galilée, valables à faible vitesse: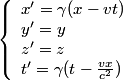
où:
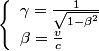
Il s'agit donc maintenant de reformuler les équations de la mécanique classique pour respecter l'invariance relativiste.
Changement de référentiel vu comme une rotation de l'espace-temps
L'on peut voir les transformations de Lorentz comme une rotation dans l'espace-temps non euclidien (Minkowskien)où:
Nous pouvons définir une autre grandeur: la rapidité phi reliée à la vitesse.
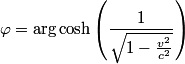
En d'autres termes, lorsque deux référentiels sont en translation rectiligne uniforme, ceux-ci voient des phénomènes tournés d'un certain angle dans l'espace-temps. Donc quand nous changeons de référentiel, c'est comme si nous tournions tout l'espace-temps d'un certain angle (ceci aura de l'importance plus tard, quand nous parlerons d'invariance de jauge globale, et locale).
Chaque grandeur en mécanique se voit attribuée une composante temporelle: quadrivitesse, quadrivecteur énergie-impulsion etc...
Un quadrivecteur se transforme d'une manière particulière dans un changement de référentiel (il est tourné).
Formulation mathématique:
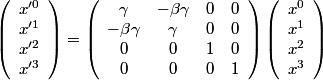
Il faut donc reformuler les lois de la mécanique classique en des lois faisant intervenir des quadrivecteurs, pour avoir des lois invariantes par transformation de Lorentz.
Quadrivecteur Vitesse
La vitesse est le quotient d'une coordonnée par le temps, qui n'est pas un quadrivecteur (lorsque l'on change de référentiel, celui-ci ne se change pas avec les transformations de Lorentz).Il existe un invariant qui a la dimension d'une longueur:
L'on peut définir une quantité qui a la dimension d'un temps:
On peut définir la quadrivitesse de la façon suivante:
ex: formulation tensorielle des équations de Maxwell.
A faible vitesse, nous devons nous assurer que les lois ainsi trouvées se réduisent en première approximation à l'analogue de la loi en mécanique classique.
4 - Dilatation des durées, Contraction des longueurs, Paradoxes
Relativité de la simultanéité
Soit deux évènements simultanés dans R (x1,t) (x2,t), ces évènements correspondent aux évènements (x'1,t'1) (x'2,t'2) dans le référentiel R' . D'après les transformations de Lorentz l'on a:
Donc deux évènements simultanés dans R ne sont pas simultanés dans R'.
Dans un train, deux évènements peuvent être vus simultanés, alors qu'ils ne le sont pas vu du quai !
Imaginons qu'un train circule sur une voie, au milieu de ce train, il y a une lampe, à l'avant de la rame l'observateur Paul, et à l'arrière Pierre. Les deux conviennent d'actionner le bouton de la radio dès qu'ils voient le signal lumineux porté par l'ampoule. Le train arrive en gare sans ralentir, et l'ampoule s'allume, à ce moment, des signaux lumineux sont émis vers l'avant et vers l'arrière, et parcourt la même distance pour atteindre Pierre et Paul simultanément pour un observateur dans le train. Pierre et Paul actionne bien le signal de la radio simultanément.
Que voit-on sur le quai ? L'ampoule s'allume et émet de la lumière vers l'avant et vers l'arrière à la vitesse de la lumière. Comme l'avant fuit la lumière, et que l'arrière va à l'encontre du signal, l'observateur du quai voit la lumière arriver en premier à l'arrière de la rame, puis ensuite la lumière arrive à l'avant. Pour l'observateur resté à quai, Pierre actionne d'abord le signal, puis ensuite c'est le tour de Paul.
En relativité restreinte, il y a relativité de la simultanéité.
Contraction des longueurs
D'après les transformations de Lorentz, une règle de longueur L dans un référentiel n'aura pas la même longueur vu dans un référentiel en mouvement. En effet, il suffit de considérer l'évènement: (x1,t) (x2,t) dans R (x1 étant l'extrémité gauche de la règle et x2 l'extrémité droite par exemple). Dans R', étant donné que la simultanéité est relative, la longueur de la règle sera différente, elle sera plus courte.
A-t-on des observations physiques du phénomène de contraction relativiste des longueurs ?
Effectivement, tous les jours, notre atmosphère est bombardée par des rayons cosmiques, ceux-ci génèrent des particules instables: les muons, qui ont une durée de vie faible: 1e-6 seconde soit 1 millième de millème de seconde. S'ils voyageaient à la vitesse de la lumière, ils auraient le temps de parcourir 300 mètres, or, ils sont créés à 20 km d'altitude.
Comment se fait-il qu'ils arrivent jusqu'à la surface de la terre ? Dans le référentiel des muons, c'est très simple, étant donné que la terre voyage quasiment à la vitesse de la lumière par rapport à eux, notre atmosphère, qui a une épaisseur de 20 km, semble moins épaisse à cause de la contraction relativiste des longueurs. Pour eux, l'atmosphère a l'air de faire quelques mètres, ou quelques centimètres.
Dilatation des durées
Toujours d'après les transformations de Lorentz, les horloges ne battent pas à la même vitesse vu de deux référentiels en mouvement.
Revenons sur la même expérience: celle de la création des muons à haute altitude. Selon l'interprétation vue de la terre, les muons subissent une dilatation relativiste des durées, ils semblent vivre plus longtemps c'est pourquoi ils peuvent atteindre la surface de la terre.
Les deux explications sont correctes et équivalentes. Ce sont des descriptions quantitatives strictement équivalentes, mais de points de vu différents dans des référentiels différents.
Paradoxes
Puisque la relativité restreinte bouleverse nos conceptions familières de l'espace et du temps, des raisonnements pas assez rigoureux peuvent nous conduire à des situations bizarres, non familières, voire fausses.
Paradoxe des jumeaux de Langevin
C'est une expérience de pensée imaginée par Albert Einstein, et dont les calculs détaillés ont été faits par Paul Langevin (physicien français). Dans cette expérience, l'on prend deux jumeaux: Franck et Fred. Franck reste sur terre, tandis que Fred part pour une planète extra solaire située à 10 années lumière, dans une capsule spéciale, puis revient. Le voyage se fait le plus confortablement possible, avec une phase où le vaisseau acquiert sa vitesse nominale, puis reste à cette vitesse pendant la majeure partie du temps. A son retour, il s'est écoulé 21 ans, Franck a vieillit de 21 ans, mais pour Fred, il ne s'est écoulé qu'une année.Ici la différence d'âge heurte le sens commun, mais en appliquant les calculs de relativité avec précaution nous tombons sur le même résultat.
La théorie de la relativité nous dit que les phénomènes sont identiques dans tous les référentiels, or, pour Fred, celui-ci est au repos, mais c'est Franck qui voyage, donc le temps doit s'écouler plus lentement dans le référentiel de Franck vu par Fred. Franck fait exactement le même raisonnement et en déduit la même chose. Comme d'après la relativité, tous les référentiels sont identiques, ils devraient avoir le même âge, or ce n'est pas du tout le cas, comment est-ce possible ?
Tout simplement parce que la relativité restreinte s'applique aux référentiels non accélérés, et que Fred, par le fait d'aller et revenir doit obligatoirement accélérer, c'est ce qui est à l'origine de la dissymétrie.
Confirmation expérimentale
L'équation la plus célèbre du monde
E=mc² est l'équation la plus célèbre du monde, mais quelle en est sa signification ? Et comment l'a-t-on établi ?L'équation fait intervenir les termes E d'énergie (en Joule), et m de masse (en kg), multipliée par la vitesse de la lumière au carré (en m/s). Cela veut dire que la masse est proportionnelle à l'énergie, ce qui veut dire que l'un peut se convertir en l'autre et vice versa.
En raison du facteur énorme que représente c² (environ 9e16 m²/s²), un kilogramme de matière renferme une quantité énorme d'énergie: près de 9 petajoules (PJ).
En relativité restreinte, la vitesse que l'on définit comme le rapport entre la distance et le temps n'est pas un quadrivecteur. Le quadrivecteur suivant permet d'avoir une vitesse relativiste:
De même que la quantité de mouvement classique, nous pouvons définir la quantité de mouvement relativiste (produit de la masse et de la quadrivitesse), obtenant le quadrivecteur énergie-impulsion.
A faible vitesse nous retrouvons bien la quantité de mouvement galiléenne. Quelle est la signification de la composante temporelle ? Faisons l'approximation des faibles vitesses et faisons un développement limité pour le facteur de Lorentz obtenant:
Multiplions la composante temporelle par c obtenant:
Nous reconnaissons l'énergie cinétique. Lorsque la vitesse est nulle, cette quantité n'est pas nulle, il existe donc une énergie de repos. Nous reconnaissons donc la célèbre équation de la relativité. La masse est proportionnelle à l'énergie.
Conséquences sur la physique nucléaire et la bombe
Vers la fin du XIXème siècle, à mesure que les instruments de mesure s'amélioraient en précision, l'on a constaté que le rapport des masses des éléments chimiques étaient dans un rapport entier (même pour le chlore par exemple, même si sa masse molaire est de 35.5 g/mole, il a été compris qu'il était constitué de deux isotopes 35 et 37 dans les proportions 3 et 1 expliquant cette masse molaire), enfin... presque, à 1% près.Grâce à la théorie d'Einstein, l'on comprend maintenant où est passée cette masse manquante. C'est en fait l'énergie de liaison des nucléons.
Donc si l'on prend 1 kg d'hydrogène et que l'on arrive à fusionner celui-ci en hélium, environ 1% de la masse totale sera libérée en énergie, soit 10g multipliée par c² soit donc: 1e15 joules (contre 3e15 joules consommation annuelle de la France). 1 kg d'hydrogène peut subvenir aux besoins énergétique de la France pendant 4 mois (contre 90 millions de tonne de pétrole).
C'est une quantité d'énergie colossale contenue dans un noyau atomique, qui a eu la macabre application militaire gravée dans l'Histoire de l'Humanité.
Accélérateurs de particules
Les premiers accélérateurs de particules étaient linéaires, l'on accélérait une particule le long de celui-ci, plus il était long, et plus l'énergie atteinte était élevée, mais ceci n'est pas très rentable, puisque la particule ne passe qu'une seule fois dans celui-ci. C'est pourquoi a été inventé le cyclotron. C'est un accélérateur constitué de deux D, générant un champ magnétique permettant de dévier des particules chargées le long d'une trajectoire circulaire. Entre les deux D règne une différence de potentiel permettant d'accélérer la particule.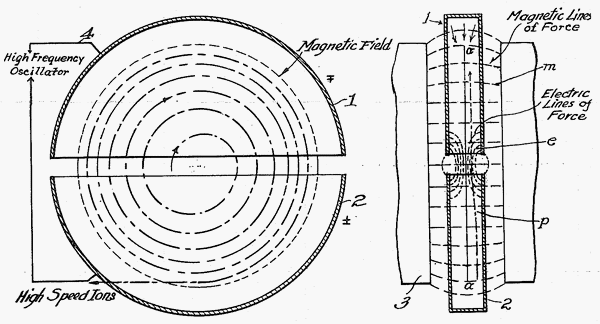
Schéma d'un cyclotron.
Ernest O. Lawrence - Method and apparatus for the acceleration of ions.
Il faut donc faire osciller la tension alimentant les électro-aimants à une fréquence précise pour accélérer la particule (il y a deux cycles par tour). Or cette fréquence dépend de la masse de la particule, lorsque celle-ci approche de façon non négligeable la vitesse de la lumière, l'on remarque que la fréquence n'est plus adaptée, la particule a l'air de devenir plus lourde, cette augmentation de la masse en fonction de la vitesse est exactement décrite par la relativité restreinte.
Il y a donc dilatation de la masse, il faut donc adapter un cyclotron en synchro cyclotron, pour "synchroniser" la bonne fréquence en fonction de la vitesse de la particule pour compenser les effets relativistes (de la relativité restreinte).
5 - La Relativité Générale
La Relativité Générale
La théorie de la gravitation de Newton, publiée en 1687 dans les "Principia Mathematica", a expliqué la chute des corps, le mouvement des planètes autour du soleil, le modèle Copernicien du système solaire, le mouvement des comètes, les lois empiriques de Képler. A mesure que les instruments d'observation s'affinaient, des décalages ont été observés, notamment l'avance de périhélie de la planète Mercure (43 secondes d'arc par siècle, même après avoir tenu compte de la perturbation des autres planètes).
Conscient des conséquences de la théorie de la relativité restreinte sur la mécanique classique, Einstein voulait s'attaquer à la théorie de la gravitation de Newton, qui n'arrivait pas à expliquer certaines anomalies (avance de périhélie de Mercure, des explications ont été avancées, notamment une ellipticité du soleil [que les érudits connaissent sous le terme J2, où une autre planète entre Mercure et le Soleil: Vulcain, perturbant son orbite]), puisque celle-ci contredisait de manière flagrante la relativité restreinte, comme quoi aucun signal ne peut se déplacer plus vite que la lumière, a fortiori, la détection d'un champ de gravitation est un signal, celui-ci ne peut pas se propager plus vite que la lumière.
Par ailleurs Einstein voulait étendre le principe de relativité à tous les types de mouvements, pas seulement rectiligne uniforme, mais également à tous les mouvements accélérés.
Le Principe d'équivalence
Aujourd'hui nous sommes tous familiers avec les ascenseurs, ou les expériences de micro-gravité dans des avions de ligne en chute libre. Nous savons que nous pouvons annuler les effets de la gravitation du moins localement. Au cinéma, dans les films de science-fiction, nous sommes également familiers avec l'absence de gravitation loin de toute planète, et que l'allumage des moteurs, provoquant un mouvement accéléré du vaisseau permet de simuler une certaine pesanteur.
Ceci est le principe d'équivalence, un mouvement accéléré peut être vu localement comme un champ de gravitation. Un observateur en chute libre, n'est plus soumis à la gravitation et les lois de la relativité restreinte s'appliquent.
On peut voir un mouvement accéléré comme une rotation dans l'espace-temps, dont l'angle dépend du point de l'espace.
Idée d'invariance de jauge locale
Nous avons vu dans la partie sur la relativité restreinte que deux observateurs en translation rectiligne uniforme ont leur repère d'espace-temps tourné d'un certain angle. En fait chaque point d'un repère est tourné du même angle phi par rapport à un autre repère. En d'autres termes dans une rotation globale de l'espace-temps, les lois de la physique sont invariantes. En termes plus techniques, nous disons que les lois de la physique doivent être invariantes par symétrie de jauge globale dans le groupe SO(3,1) (c'est un groupe de symétrie orthogonale, les matrices sont de dimension 4).
Pour un mouvement accéléré, nous voyons que la vitesse varie en fonction du point. En fait l'on peut considérer une rotation qui dépend du point de l'espace-temps. Einstein a postulé que les lois de la physique restent également invariantes par une rotation quelconque, l'on dit que les lois de la physique doivent être invariantes par une symétrie de jauge locale SO(3,1) (c'est une rotation quelconque dans l'espace-temps, angle qui dépend du point).
Fort de cette idée, Einstein a donc imaginé un rayon de lumière vu par un observateur en chute libre. En l'absence de champ de gravitation la lumière se déplace en ligne droite, alors dans un champ de gravitation la lumière doit voyager sur une trajectoire courbe. L'espace-temps doit être courbe !
Conséquence sur l'Espace-Temps
Pour développer la théorie, il faut donc utiliser les mathématiques des espaces courbes développées au XVIIIème siècle par des mathématiciens comme Carl Friedich Gauss(1777-1865), Nicolaï Lobatchevsky (1792-1856), Janos Bolyai (1802-1860), et Bernhard Riemann (1826-1866), formalismes très adaptés à la relativité générale.
Heureusement à l'école polytechnique fédérale de Zurich (EPFZ), Einstein a gardé contact avec un très bon ami: le mathématicien Marcel Grosmann, qui le formera à sa spécialité: les espaces de Riemann.
Annexe Mathématique
Espace-Temps de Minkowski
Nous pouvons écrire les équations de la relativité restreinte sous forme tensorielle.L'espace-temps de Minkowski est, plat, dépourvu de matière. Dans cet espace non euclidien, nous pouvons écrire le produit scalaire de la façon décrite dans le section précédente, faisant intervenir le tenseur métrique suivant:
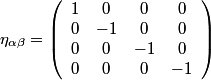
Métrique
Ce tenseur est la métrique d'un espace-temps plat. Il permet de mesurer des longueurs connaissant les composantes d'un vecteur ou quadrivecteur. Dans un espace-temps courbe, le tenseur métrique dépend de la position.Dérivée covariante, et Coefficients de Christoffel
Les équations de la relativité restreinte sont bien invariantes par rotation d'un angle constant dans l'espace-temps. Mais pour qu'elles respectent le principe d'équivalence, il faut modifier ces équations afin qu'elles soient invariantes dans un espace-temps courbe. La dérivée traditionnelle n'a pas un caractère covariant (elle ne garde pas la même forme lorsque l'on change de référentiel, puisqu'elle ne prend pas en compte la variation des vecteurs de sa base locale).La dérivée ainsi définie permet de prendre en compte la courbure de l'espace. En effet, pour connaître comment varie un vecteur, il ne suffit pas de savoir comment varient ses composantes, il faut également voir comment varient les vecteurs bases de l'espace (c'est ce qui explique le terme supplémentaire).
Où les coefficients de Christoffel s'écrivent:
Dans un espace courbe, il n'y a plus de ligne droite, les équations donnant les géodésiques (chemin le plus court entre deux points) sont:
Courbure
Comment peut-on caractériser un espace courbe de manière locale ? Il suffit de transporter un vecteur vers un point, en parcourant 2 chemins différents, chemins caractérisés par 2 directions que l'on alterne (ex: Nord puis Est, ou bien Est puis Nord), et de comparer leur direction, obtenant:Les coefficients de Christoffel n'ont pas un caractère tensoriel. Nous pouvons donc définir un tenseur, permettant de caractériser la courbure de l'espace-temps:
Tenseur énergie impulsion
En relativité restreinte, il y a un tenseur important: le tenseur énergie-impulsion. Celui-ci permet de caractériser la distribution de matière et d'énergie, sources d'un champ gravitationnel. Celui-ci peut être défini pour un fluide parfait (densité d'énergie, pression), ou tout simplement en utilisant le Lagrangien du système. Nous ne donnerons pas de définition ici.L'expression en relativité restreinte de la conservation de l'énergie-impulsion s'écrit de la façon suivante:
Ce tenseur est symétrique et d'ordre 2. En relativité générale, la dérivée covariante de ce tenseur doit être nulle.
Nous pouvons maintenant formaliser l'intuition d'Einstein, et donc relier la distribution de matière (le tenseur énergie-impulsion) à la courbure de l'espace-temps. Pour cela, il faut trouver un tenseur d'ordre 2 symétrique, ayant une dérivée covariante nulle, incluant des propriétés de courbures (donc un tenseur d'ordre 2 dérivé du tenseur d'ordre 4 de courbure).
Equation d'Einstein
A partir du tenseur de Riemann, il est possible de le contracter pour obtenir un tenseur d'ordre 2, symétrique. De là nous pouvons construire un tenseur de dérivée covariante nulle, c'est exactement celui qu'il nous faut pour relier la distribution de masse et d'énergie et la courbure de l'espace-temps:
La relativité générale relie la distribution de l'énergie et de la matière à la courbure de l'espace-temps.
Commentaire sur l'équation
Cette équation est extrêmement simple et extrêmement belle. En partant de l'hypothèse comme quoi les lois de la physique sont les mêmes dans tous les référentiels, accélérés ou non, et du postulat du principe d'équivalence (qui est une très belle symétrie de jauge locale), nous aboutissons à une équation qui nous dit que la distribution de matière pilote la courbure de l'espace-temps. La matière dit à l'espace comment se courber, et l'espace dit à la matière comment se mouvoir.
Solution de Schwarzschild
Karl Schwarzschild est un physicien allemand. Engagé en tant qu'artilleur sur le front russe pendant la première guerre mondiale, il a pu résoudre les équations d'Einstein entre deux calculs de balistique, obtenant la métrique éponyme. Il est mort suite à une maladie contractée pendant la guerre sur le front en 1916.
Cette solution est valable à l'extérieur d'une source à symétrie sphérique. Elle montre qu'en deçà d'un rayon particulier, la métrique s'affole.
Ondes gravitationnelles
Tout comme les équations de Maxwell, les équations d'Einstein permettent l'existence d'une métrique non plate en l'absence de source de gravitation. Ces perturbations se propagent à la vitesse de la lumière, ce sont des perturbations de l'espace et du temps, ou des rides d'espace-temps.
Il est possible de faire un calcul analytique en supposant l'espace-temps plat, et supposer ses rides de faibles amplitudes.
6 - Confirmations Expérimentales
Avance du Périhélie de Mercure
Vers la fin du XIXème siècle, à mesure que les instruments et les observations se sont affinées, les scientifiques ont remarqué des décalages par rapport aux lois de Newton, notamment l'avance de périhélie de Mercure. Même en rajoutant la contribution des autres planètes, il subsiste un petit décalage de 43 secondes d'arc par siècle.
Après avoir écrit ses équations, Einstein s'est empressé de calculer cette avance de périhélie et a trouvé exactement 43 secondes d'arc par siècle, ceci l'a conforté dans le pouvoir explicatif de la théorie de la relativité générale fraîchement échafaudée.
Expédition d'Eddington
La théorie de la relativité générale prédit une courbure de l'espace-temps importante au voisinage d'un astre massif. L'astre le plus massif, le plus près de nous est le Soleil, et il est facile de vérifier si l'espace est bien courbe. En effet, il suffit de comparer la position des étoiles lorsque le Soleil est absent, et lorsque le Soleil est présent dans la même partie du ciel (donc à 6 mois d'intervalle), les étoiles les plus près angulairement parlant seront les plus déviées. Or au lendemain de la première guerre mondiale, il y avait une éclipse totale du Soleil (en 1919). Cet évènement est idéal pour vérifier les prédictions de la relativité générale. Plusieurs expéditions ont été financées, et Arthur Eddington a pu prendre des clichés afin de vérifier la prédiction de la relativité générale.
Du jour au lendemain, Albert Einstein est devenu connu du grand public en faisant la une des journaux.
L'expérience de Pound-Rebka
L'expérience établie en 1959 utilise comme source la désexcitation d'un noyau de Cobalt 57 dans le domaine gamma. Les expérimentateurs ont constaté une variation de la fréquence émise entre le sommet et le bas d'un immeuble de seulement 22.5 mètres, avec une marge d'erreur de 10% conformément aux prévisions de la relativité générale.
Ralentissement des horloges dans un champ de gravitation
De manière anecdotique, une fusée a également été envoyée à 10 000 km d'altitude en 1976, avec à son bord une horloge atomique équipée d'un maser à hydrogène. Il a été alors possible de comparer la cadence de cette horloge et de celle identique restée sur terre. Cela a également confirmé à 0.007% près un ralentissement des horloges dans un champ de gravitation.
Entraînement de l'espace temps gravity probe B
En 2004, une sonde a été lancée: Gravity Probe B, équipée de gyroscope avec des sphères de silicium. La sonde était programmée pour fonctionner 1 an afin de récolter assez de données pour démontrer un autre effet de la relativité générale: l'effet Lense-Thirring, ou l'entraînement de l'espace-temps au voisinage de la terre.
En 2005 les premiers résultats ont permis de conclure qu'un effet de ce genre existe, mais les données trop bruitées ne permettent pas de confirmer avec une précision suffisante les prédictions de la relativité générale.
Système binaire de pulsars
Un pulsar est une étoile à neutron tournant rapidement sur elle-même, émettant des ondes électromagnétiques dans la direction de ses pôles magnétiques, qui ne coïncident pas forcément avec son axe de rotation, c'est pourquoi nous les voyons clignoter. Les étoiles sont souvent doubles, ou triples, et il arrive parfois que des systèmes doubles d'étoiles similaires deviennent presqu'en même temps des étoiles à neutrons, formant un système double de pulsar.
Un certain nombre a été observé, et plus précisément PSR B1913+16. Il se trouve que ce système voit sa période diminuer, ce qui est inexplicable par les lois de Newton. Selon la relativité générale, un système n'ayant pas de symétrie sphérique doit émettre des ondes gravitationnelles, et donc perdre de l'énergie, donc l'orbite doit rétrécir et la période diminuer. Des mesures ont été faites pour connaître précisément la masse du système double, le rayon de l'orbite, etc... et Hulse et Taylor ont calculé la diminution de la période prédite par la relativité générale en 1974, trouvant une diminution de la période conforme aux observations. Ceci leur a valu le prix nobel de physique en 1993. Ceci confirme de manière flagrante la relativité générale, mais démontre de manière indirecte l'existence des ondes gravitationnelles.
Existence de trous noirs
Dans la solution de Schwarzschild, il existe un point où la métrique n'est plus très bien définie. Par un changement de variable adéquat, il n'en est rien. En fait la relativité générale admet une courbure infinie au centre de ces astres ce qui n'a pas trop de sens. Cependant, des astres ayant un rayon inférieur au rayon de Schwarzschild existent bien, comme par exemple au centre de la Voie Lactée, ou dans d'autres régions du ciel dénommées X, comme Cygnus-X1 ou Saggitarus-X1 etc...
De nos jours plus personne ne doute de l'existence des trous noirs, même si l'on n'en a toujours pas observé directement.
Ondes gravitationnelles
Dans un espace vide, il est possible que les composantes du tenseur métrique soient différentes du tenseur de Minkowski. Ces perturbations se propagent à la vitesse de la lumière. Ce sont des ondes gravitationnelles. Ces rides de l'espace-temps sont une prédiction de la relativité générale non encore directement observées.
Plusieurs expériences internationales sont actuellement en cours: VIRGO, LIGO, LISA. Elles sont toutes basées sur le même principe, l'interférométrie. En effet, pour détecter le passage d'une onde gravitationnelle, il suffit de détecter des variations de longueurs, pour cela, il suffit de régler un interféromètre, et de contrôler la figure d'interférence.
VIRGO est un projet franco italien construit près de Pise, les bras font 3 kilomètres de long, et le détecteur est en service depuis 2003.
LIGO (Laser Interferometer Gravitational-Wave Observatory) est un projet américain, composé de deux interféromètres séparés de 3000 km, dont les bras font 4 km.
LISA est un projet de l'ESA pour 2018, c'est un interféromètre spatial avec des bras d'une longueur de 50 millions de km.
7 - Conclusion
La théorie de la relativité générale est une généralisation du principe de relativité échafaudée par Galilée au XVIIème siècle, qui a permis d'être généralisée en une théorie de la gravitation, bouleversant nos concepts d'espace et de temps, répondant à certaines questions sur le médiateur de cette force, qui est l'étoffe de l'espace-temps lui même. Elle a été élaborée par un seul homme, en 10 ans, guidé par des considérations d'ordre esthétique, et mathématique, fruit d'une profonde réflexion sur les lois de la physique.
Cependant cette révolution n'est pas achevée, puisque la physique a connu deux grands bouleversements à l'aube du XXème siècle: la relativité, mais également la mécanique quantique. Pour qu'une théorie puisse décrire tous les phénomènes naturels, elle doit contenir les idées de la physique relativiste (formalisme covariant), mais également les lois de l'infiniment petit (formalisme quantique).
Aujourd'hui 3 des 4 interactions fondamentales sont bien décrites dans ce formalisme de la théorie quantique des champs. Cependant, la prise en compte des phénomènes quantiques dans la description de la gravitation est toujours manquante. Aujourd'hui plusieurs pistes sont âprement arpentées par les plus grands physiciens: théorie des cordes, gravitation quantique à boucles, géométries non-commutatives, théorie des twistors, mousse de spins, etc... mais nous souffrons de données expérimentales suffisantes pour guider les théoriciens.
Cours de relativité générale pour débutants de Michel le Bellac:
http://hal.archives-ouvertes.fr/docs/00 ... cel-33.pdf
Cours de RG de Bernard Linet:
http://www.phys.univ-tours.fr/~linet/
Lecture Notes on General Relativity Sean M. Carroll
http://fr.arxiv.org/abs/gr-qc/9712019
Kip Thorne: Trous noirs et distorsions du temps
ISBN 2070744655
Stephen Hawking & Roger Pensrose: La nature de l'espace et du temps
ISBN 2-07-074465-5
Lee Smolin: How far are we from Quantum Gravity ?
http://arxiv.org/abs/hep-th/0303185
Logo du dossier
Wikipedia sous Licence GNU 1.2
Cependant cette révolution n'est pas achevée, puisque la physique a connu deux grands bouleversements à l'aube du XXème siècle: la relativité, mais également la mécanique quantique. Pour qu'une théorie puisse décrire tous les phénomènes naturels, elle doit contenir les idées de la physique relativiste (formalisme covariant), mais également les lois de l'infiniment petit (formalisme quantique).
Aujourd'hui 3 des 4 interactions fondamentales sont bien décrites dans ce formalisme de la théorie quantique des champs. Cependant, la prise en compte des phénomènes quantiques dans la description de la gravitation est toujours manquante. Aujourd'hui plusieurs pistes sont âprement arpentées par les plus grands physiciens: théorie des cordes, gravitation quantique à boucles, géométries non-commutatives, théorie des twistors, mousse de spins, etc... mais nous souffrons de données expérimentales suffisantes pour guider les théoriciens.
Sources
Cours de relativité générale pour débutants de Michel le Bellac:
http://hal.archives-ouvertes.fr/docs/00 ... cel-33.pdf
Cours de RG de Bernard Linet:
http://www.phys.univ-tours.fr/~linet/
Lecture Notes on General Relativity Sean M. Carroll
http://fr.arxiv.org/abs/gr-qc/9712019
Kip Thorne: Trous noirs et distorsions du temps
ISBN 2070744655
Stephen Hawking & Roger Pensrose: La nature de l'espace et du temps
ISBN 2-07-074465-5
Lee Smolin: How far are we from Quantum Gravity ?
http://arxiv.org/abs/hep-th/0303185
Logo du dossier
Wikipedia sous Licence GNU 1.2
La Relativité