Analyse discriminante linéaire - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
L’analyse discriminante linéaire fait partie des techniques d’analyse discriminante prédictive. Il s’agit d’expliquer et de prédire l’appartenance d’un individu à une classe (groupe) prédéfinie à partir de ses caractéristiques mesurées à l’aide de variables prédictives.
Dans l’exemple de l'article Analyse discriminante, le fichier Flea Beetles, l’objectif est de déterminer l’appartenance de puces à telle ou telle espèce à partir de la largeur et de l’angle de son aedeagus.
La variable à prédire est forcément catégorielle (discrète), elle possède 3 modalités dans notre exemple. Les variables prédictives sont a priori toutes continues. Il est néanmoins possible de traiter les variables prédictives discrètes moyennant une préparation adéquate des données.
L’analyse discriminante linéaire peut être comparée aux méthodes supervisées développées en apprentissage automatique et à la régression logistique développée en statistique.
Hypothèses et Formules
Nous disposons d’un échantillon de
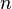
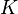
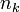
Notons
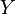
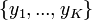
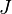
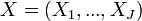
Nous notons
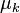
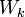
La règle bayesienne
L’objectif est de produire une règle d’affectation

La règle bayesienne consiste à produire une estimation de la probabilité a posteriori d’affectation




La règle d’affectation pour un individu ω à classer devient alors

![y_k^* = arg\; max_{k}\ P[Y(\omega)=y_k/X(\omega)]](https://static.techno-science.net/illustration/Definitions/autres/b/bf7c552423fbb7bfc9d60196103361c2_f00c9618fa70a8668025971575c5870a.png)
Toute la problématique de l’analyse discriminante revient alors à proposer une estimation de la quantité

L'analyse discriminante paramétrique - L'hypothèse de multinormalité
On distingue principalement deux approches pour estimer correctement la distribution

- L’approche non-paramétrique n’effectue aucune hypothèse sur cette distribution mais propose une procédure d’estimation locale des probabilités, au voisinage de l’observation
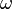
- La seconde approche effectue une hypothèse sur la distribution des nuages de points conditionnels, on parle dans ce cas d’analyse discriminante paramétrique. L’hypothèse la plus communément utilisée est sans aucun doute l’hypothèse de multinormalité (voir loi normale).
Dans le cas de la loi normale multidimensionnelle, la distribution des nuages de points conditionnels s’écrit

où


L’objectif étant de déterminer le maximum de la probabilité a posteriori d’affectation, nous pouvons négliger tout ce qui ne dépend pas de k. En passant au logarithme, nous obtenons le score discriminant qui est proportionnel à

![D[Y=y_k,X] = 2 \times Ln[P(Y=y_k)] - Ln |W_k| - (X-\mu_k)'W_k^{-1}(X-\mu_k)](https://static.techno-science.net/illustration/Definitions/autres/0/0561f485c583c48a42923b2a1a6b1fac_30d23d55cb754366abbac7e20e94da2f.png)
La règle d’affectation devient donc

![y_k^* = arg\, max_k\, D[Y(w) = y_k,X(w)]](https://static.techno-science.net/illustration/Definitions/autres/4/4182f7569affc5a5435763abd2e03b3d_c5060e1f2e5e9a62f81019924b112dfe.png)
Si l’on développe complètement le score discriminant, nous constatons qu’il s’exprime en fonction du carré et du produit croisé entre les variables prédictives. On parle alors d’analyse discriminante quadratique. Très utilisée en recherche car elle se comporte très bien, en termes de performances, par rapport aux autres méthodes, elle est moins répandue auprès des praticiens. En effet, l’expression du score discriminant étant assez complexe, il est difficile de discerner clairement le sens de la causalité entre les variables prédictives et la classe d’appartenance. Il est notamment mal aisé de distinguer les variables réellement déterminantes dans le classement, l’interprétation des résultats est assez périlleuse.
L’analyse discriminante linéaire – L’hypothèse d’homoscédasticité
Une seconde hypothèse permet de simplifier encore les calculs, c’est l’hypothèse d’homoscédasticité : les matrices de variances co-variances sont identiques d’un groupe à l’autre. Géométriquement, cela veut dire que les nuages de points ont la même forme (et volume) dans l’espace de représentation.
La matrice de variance co-variance estimée est dans ce cas la matrice de variance co-variance intra-classes calculée à l’aide de l’expression suivante

De nouveau, nous pouvons évacuer du score discriminant tout ce qui ne dépend plus de k, il devient
![D[Y=y_k,X] = 2 \times Ln[P(Y=y_k)] - (X-\mu_k)'W^{-1}(X-\mu_k)](https://static.techno-science.net/illustration/Definitions/autres/6/6e97db7895cb4588e44ac4ab2eb3b3de_eef021c735b09b33ffcbdcb97a1c02d0.png)
Fonction de classement linéaire
En développant l’expression du score discriminant après introduction de l’hypothèse d’homoscédasticité, on constate qu’elle s’exprime linéairement par rapport aux variables prédictives.
Nous disposons donc d’autant de fonctions de classement que de modalités de la variable à prédire, ce sont des combinaisons linéaires de la forme suivante :



Cette présentation est séduisante à plus d’un titre. Il est possible, en étudiant la valeur et le signe des coefficients, de déterminer le sens des causalités dans le classement. De même, il devient possible, comme nous le verrons plus loin, d’évaluer le rôle significatif des variables dans la prédiction.
Robustesse
Les hypothèses de multinormalité et d’homoscédasticité peuvent sembler trop contraignantes, restreignant la portée de l’analyse discriminante linéaire dans la pratique.
La notion clé qu’il faut retenir en statistique est la notion de robustesse. Même si les hypothèses de départ ne sont pas trop respectées, une méthode peut quand même s’appliquer. C’est le cas de l’analyse discriminante linéaire. Le plus important est de le considérer comme un séparateur linéaire. Dans ce cas, si les nuages de points sont séparables linéairement dans l’espace de représentation, elle peut fonctionner correctement.
Par rapport aux autres techniques linéaires telles que la régression logistique, l’analyse discriminante présente des performances comparables. Elle peut être lésée néanmoins lorsque l’hypothèse d’homoscédasticité est très fortement violée.

















































