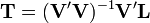Analyse procustéenne - Définition

Introduction

En statistiques, l'analyse procustéenne est une technique pour comparer des formes. Elle est utilisée pour déformer un objet afin de le rendre autant que faire se peut semblable à une référence (potentiellement arbitraire), ne laissant apparaître entre l'objet et la référence que les différences que les transformations autorisées (rotation, translation et mise à l'échelle) n'ont pu gommer. La déformation supprime les différences qui ne sont pas dues à la forme intrinsèque de l'objet (mais par exemple à un biais introduit lors de l'acquisition des données). Celles qui subsistent sont considérées objectives, et permettent d'évaluer le degré de ressemblance entre l'objet et la référence.

Cette technique a été nommée ainsi en 1962 par Hurley et Catell à partir de Procuste, un bandit de la mythologie grecque qui forçait ses victimes à s'allonger sur un lit et modifiait violemment leur taille pour que celle-ci corresponde à la taille du lit. Cependant, le cœur théorique de la technique est de plus de 20 ans antérieur (Mosier, 1939). Améliorée et affinée depuis par de nombreuses publications scientifiques, l'analyse procustéenne est utilisée dans tous les champs où l'analyse de formes peut être utile, à l'instar entre autres de la biologie, de l'archéologie et de la médecine.

Le problème de Procuste

Procuste, personnage de la mythologie grecque, était un bandit qui forçait ses victimes à s'allonger sur son lit et les étirait si celles-ci étaient plus petites que le lit, ou coupait avec sa hache ce qui dépassait si celles-ci étaient plus grande.

La version scientifique de l'histoire, dans le domaine de l'analyse des formes, consiste à se donner pour lit une forme de référence, dont les propriétés sont connues, sur lequel on allongera des victimes venant d'un ensemble d'objets à étudier. Le problème consiste à comparer la forme du lit à la forme des victimes, opération difficile tant que l'une ne peut pas s'allonger sur l'autre.

Pour retailler les victimes et résoudre le problème, les scientifiques vont utiliser, en fait de hache, la translation, qui permettra de déplacer les victimes jusqu'au centre du lit, l'homothétie, qui changera la taille de la victime pour qu'elle soit égale à la taille du lit et enfin la rotation, qui trouvera la position la plus confortable pour la victime.

Il apparaît ainsi que la hache ne peut changer la forme de l'objet (toutes les transformations utilisées conservent les angles). Cela permet par exemple en biologie de comparer la forme du crâne d'un dauphin et d'un rat, en éliminant la différence de taille entre ces deux crânes, ainsi que les différences introduites lors de la numérisation des données (position et orientation sur l'appareil de mesure, par exemple).

Illustration en dimension deux

Illustration de l'analyse : un carré de référence en bleu et un quadrilatère à analyser en vert

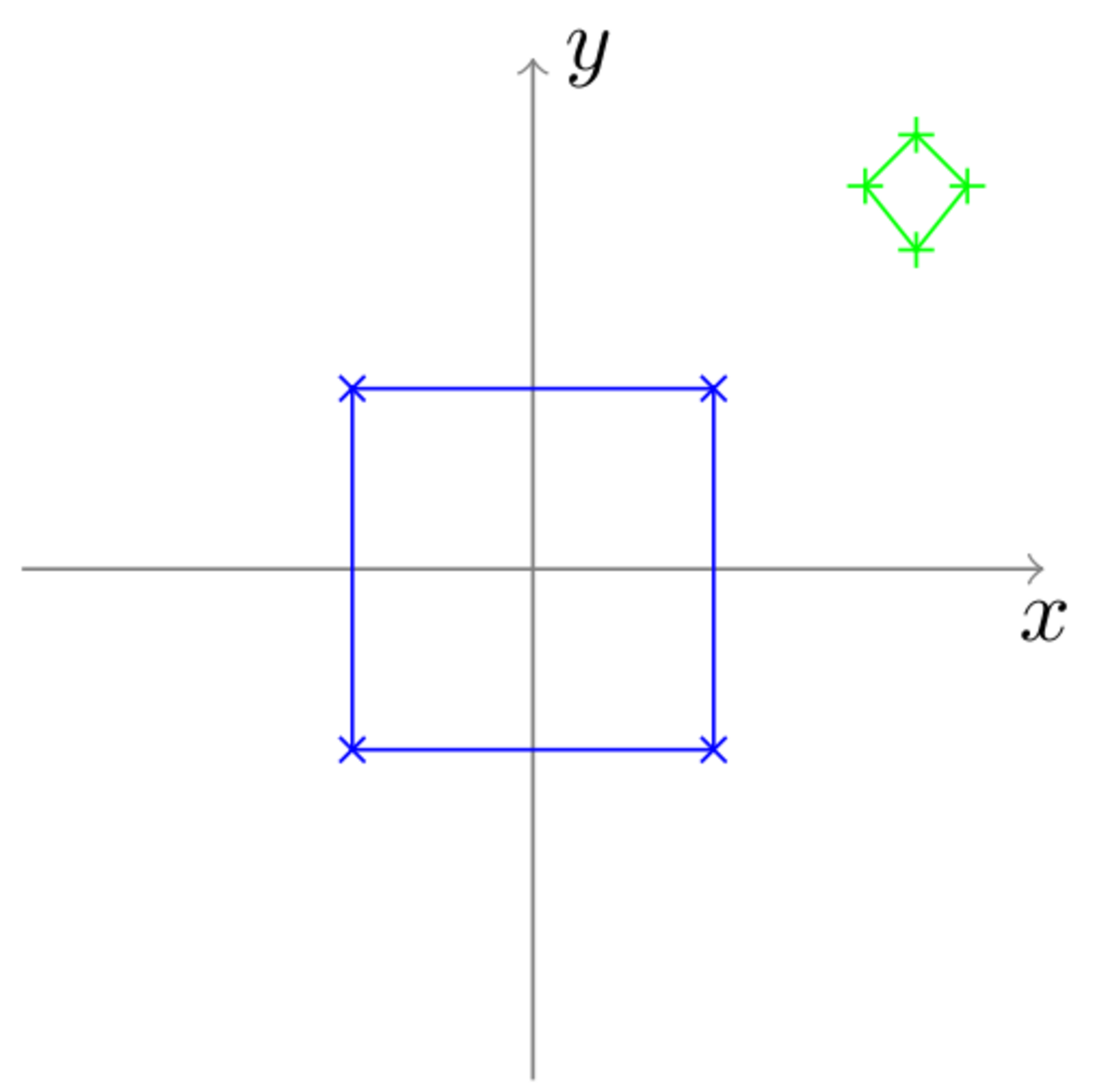
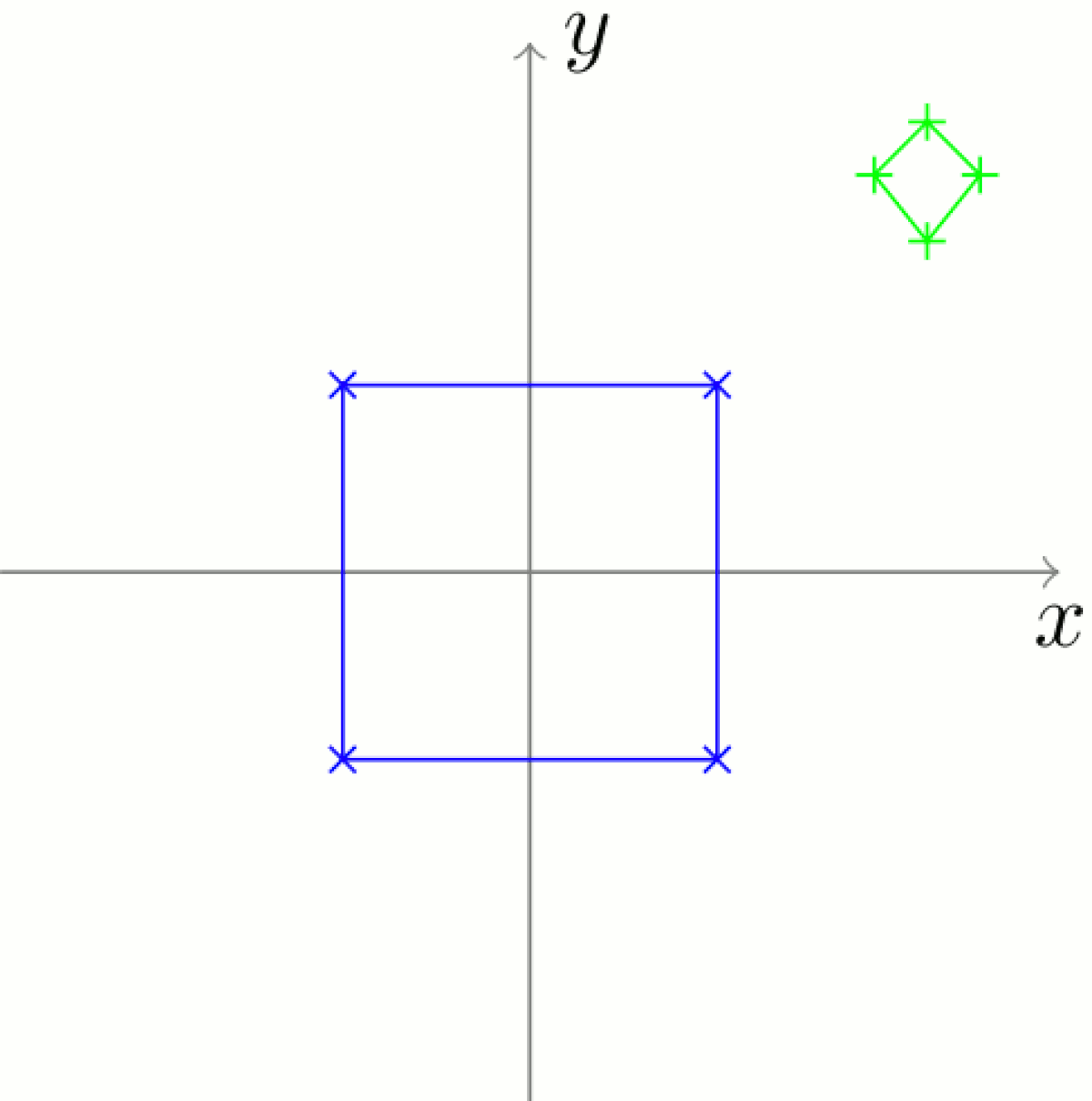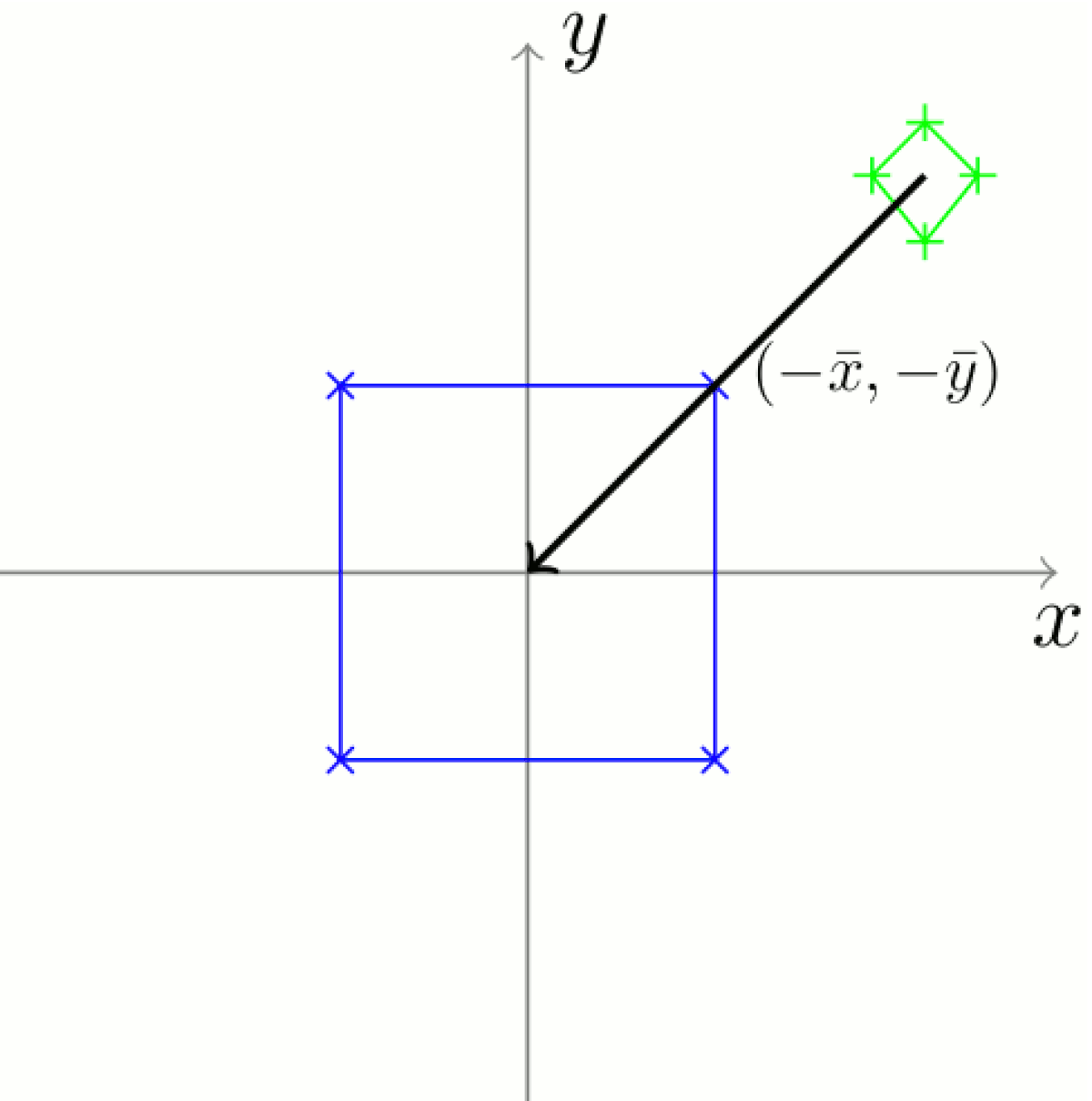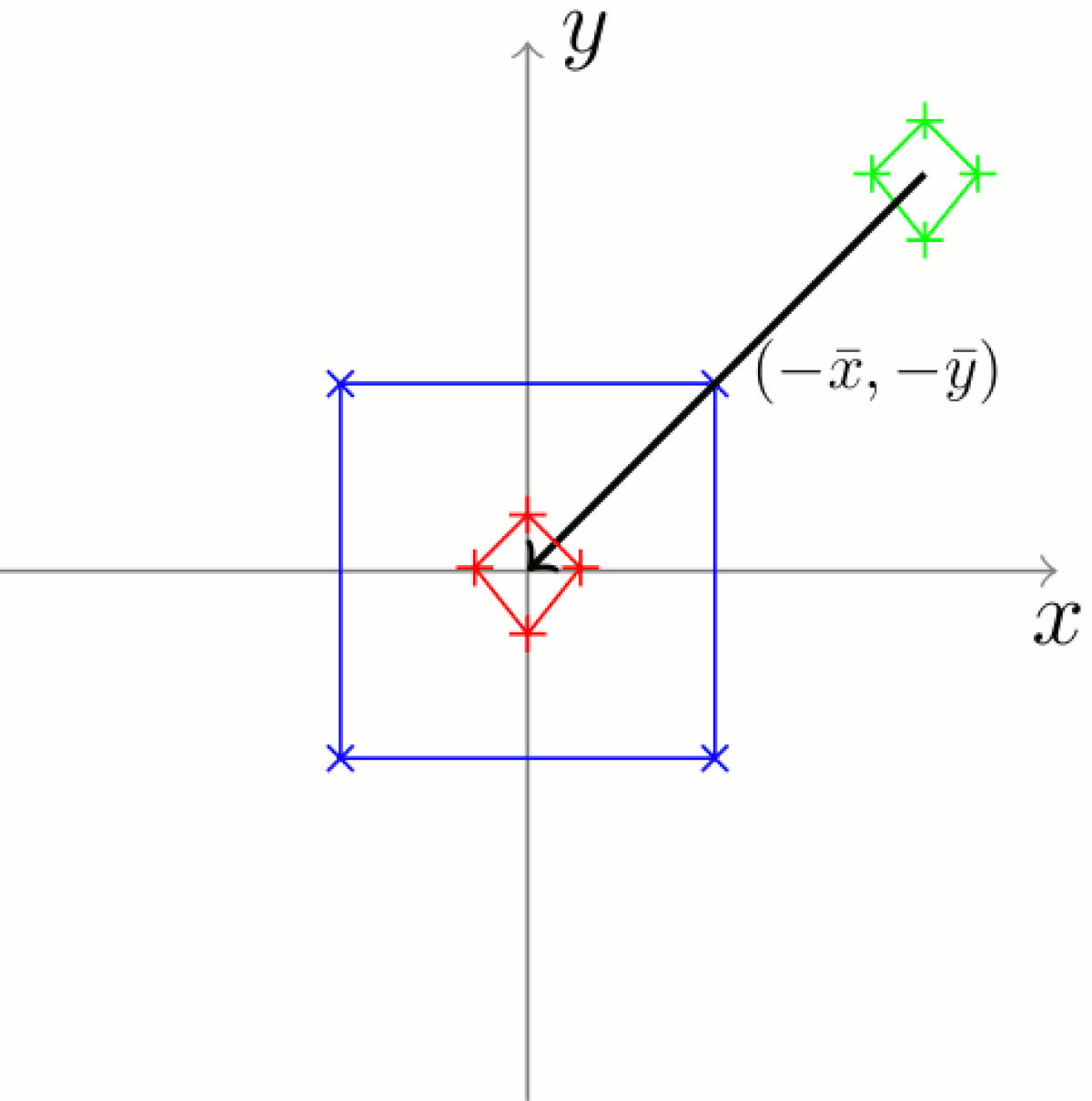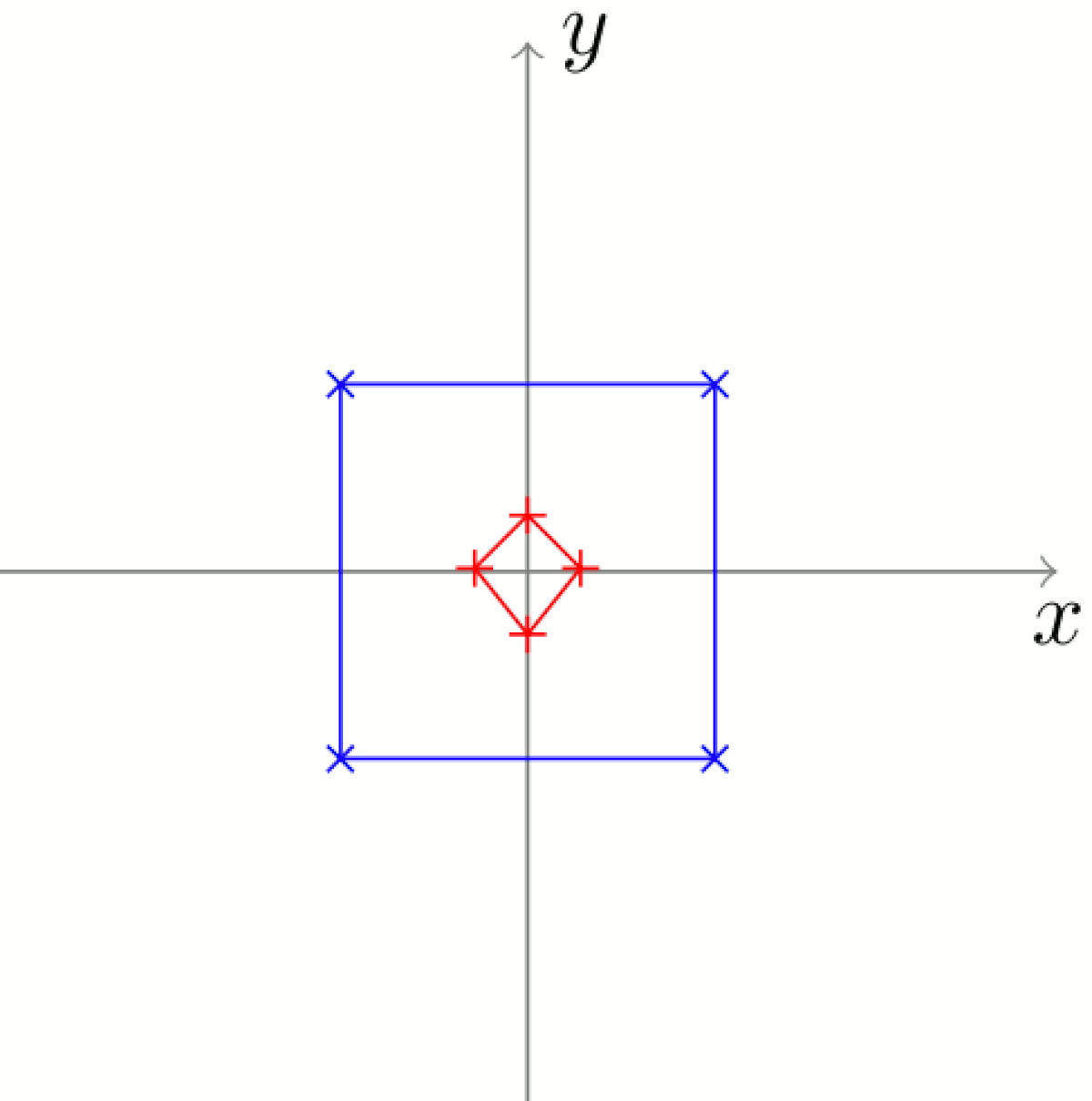
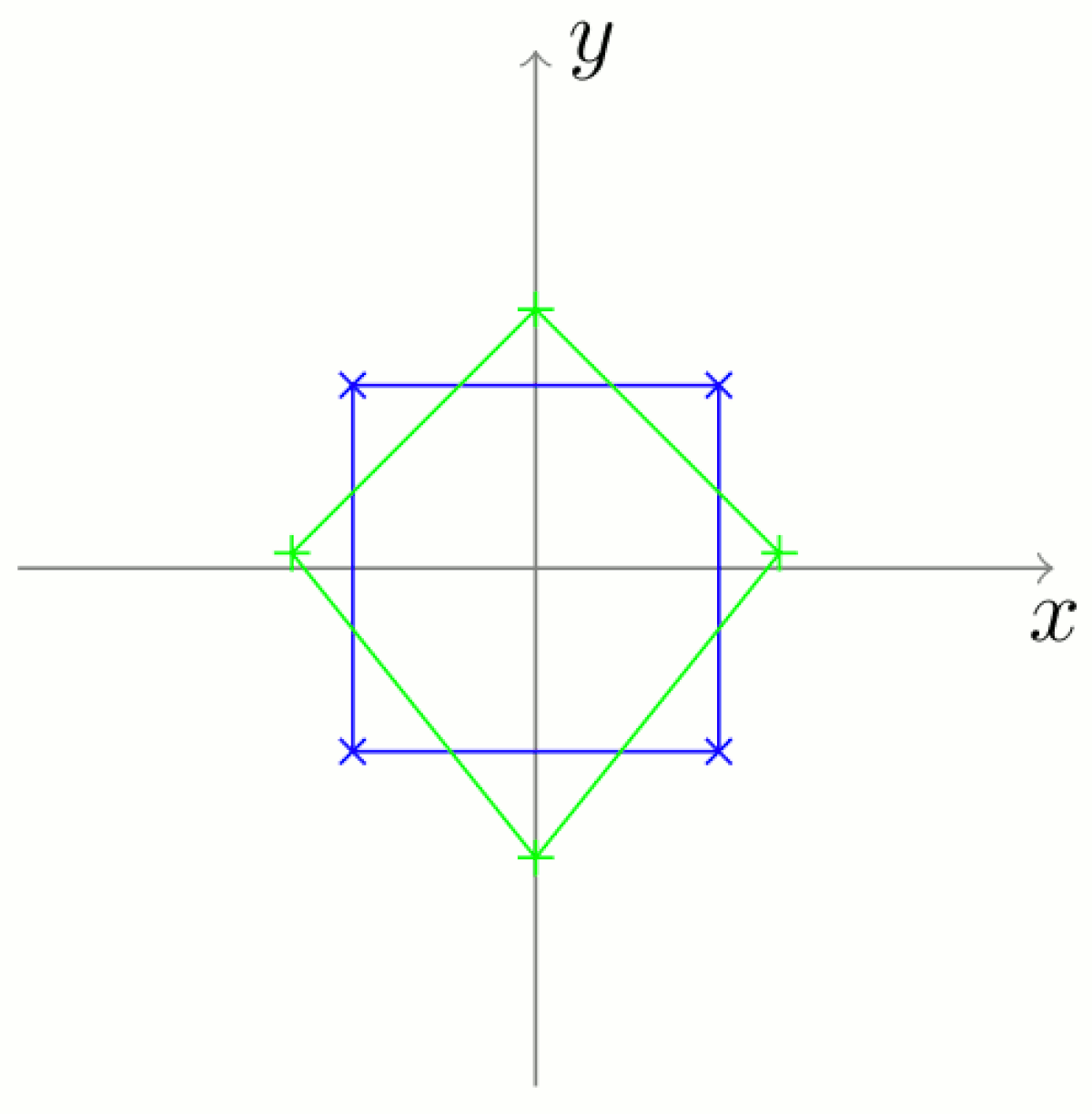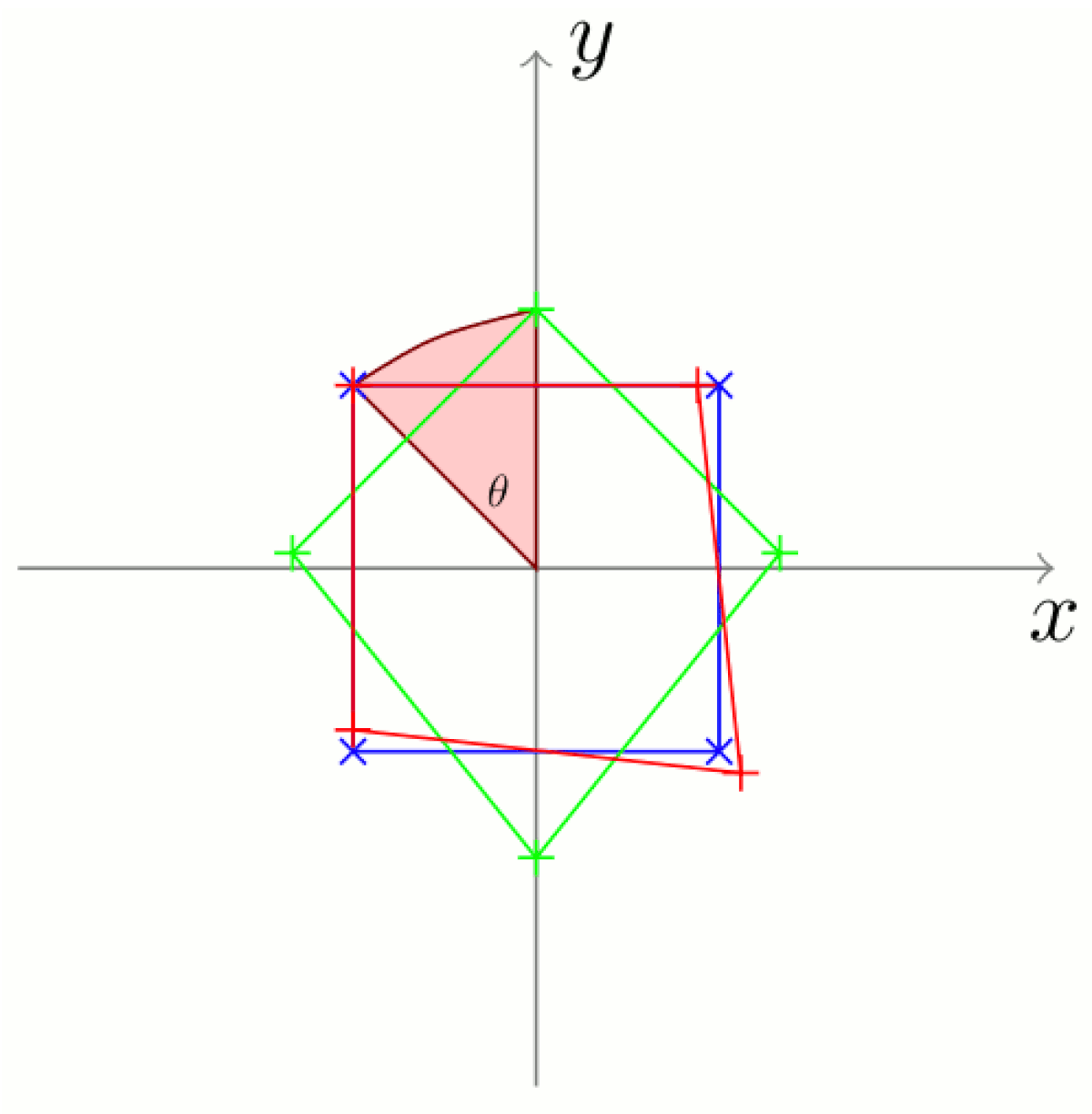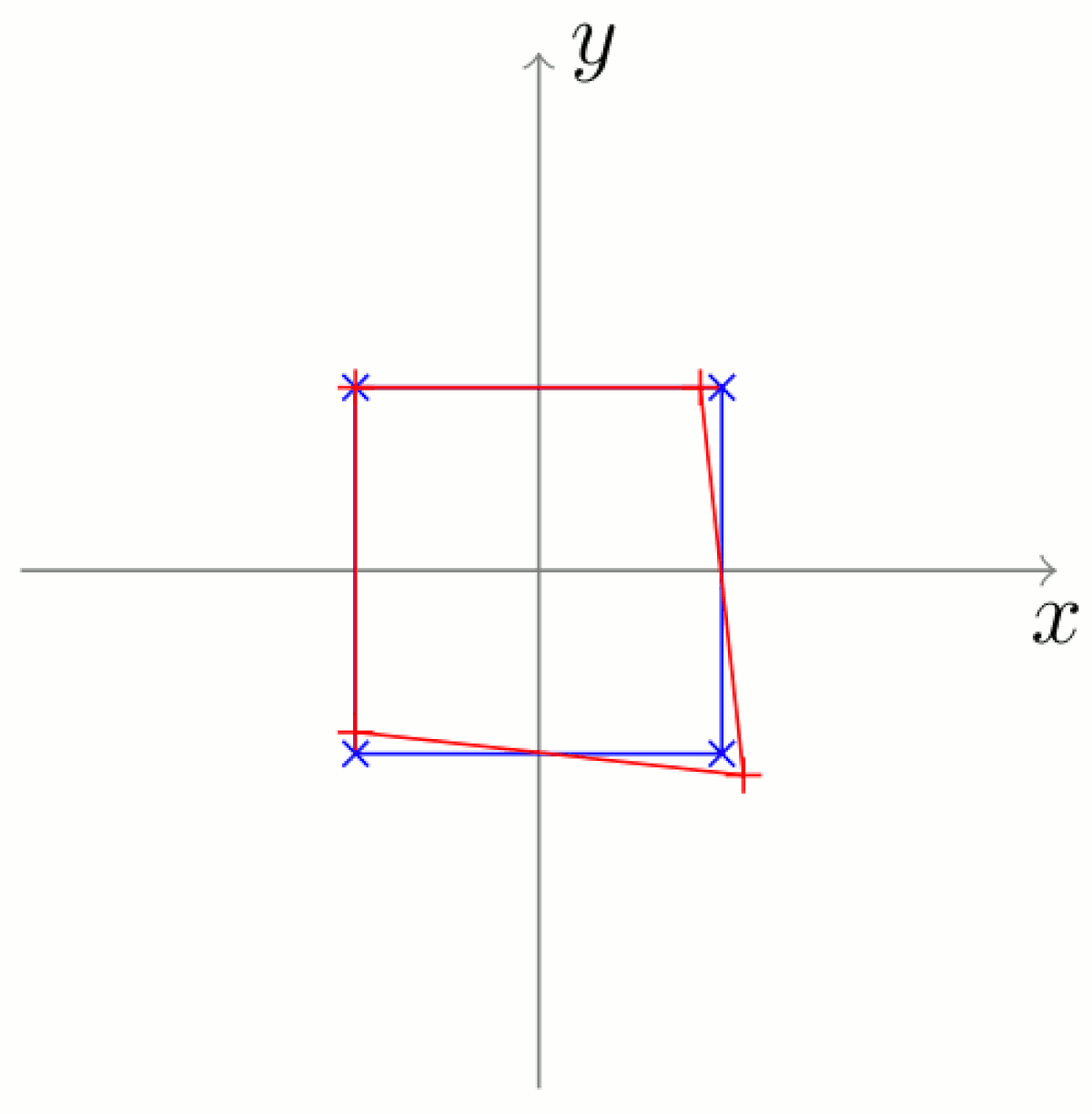
La première étape en analyse Procuste est de rechercher, dans la forme à étudier, un certain nombre de points considérés comme des points de référence ou points d'intérêts qui pourront résumer la forme étudiée. Pour illustrer la résolution du problème de Procuste, on peut considérer le cas d'une victime, symbolisée par les quatre points du quadrilatère vert sur le schéma, que l'on cherche à allonger sur un lit carré (en bleu sur le schéma), de côté 1, centré sur l'origine.

La méthode de base, illustrée ici, consiste en la suppression des trois composantes en translation, rotation et échelle du quadrilatère vert. La seule contrainte sur l'ordre des opérations est que la rotation doit être effectuée en dernier.

Suppression de la composante en translation

Le quadrilatère à analyser est centré sur l'origine grâce à la translation

La forme à analyser et la référence sont maintenant toutes deux centrées sur l'origine.

Il faut que le centre du quadrilatère considéré coïncide avec le centre de la forme de référence, qui se situe à l'origine du repère. Pour cela, il suffit de calculer les coordonnées du centre du quadrilatère vert :

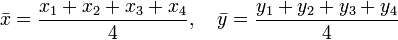
où sont les coordonnées des quatre sommets du quadrilatère vert, puis d'appliquer à tous ces points la transformation  :

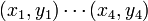
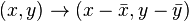
Suppression de la composante d'échelle

La surface du quadrilatère à analyser est rendue égale à celle du carré de référence (qui vaut 1).

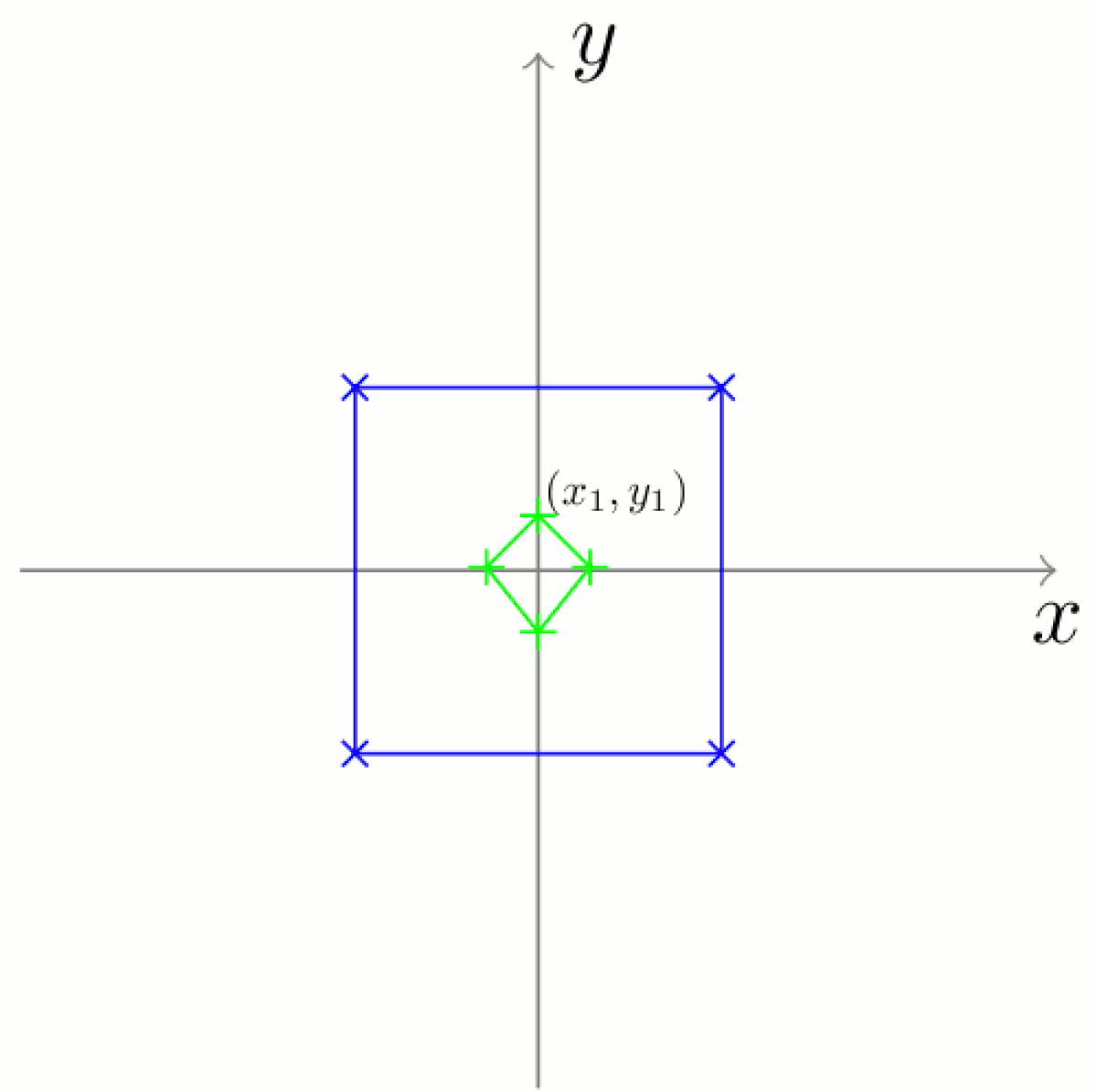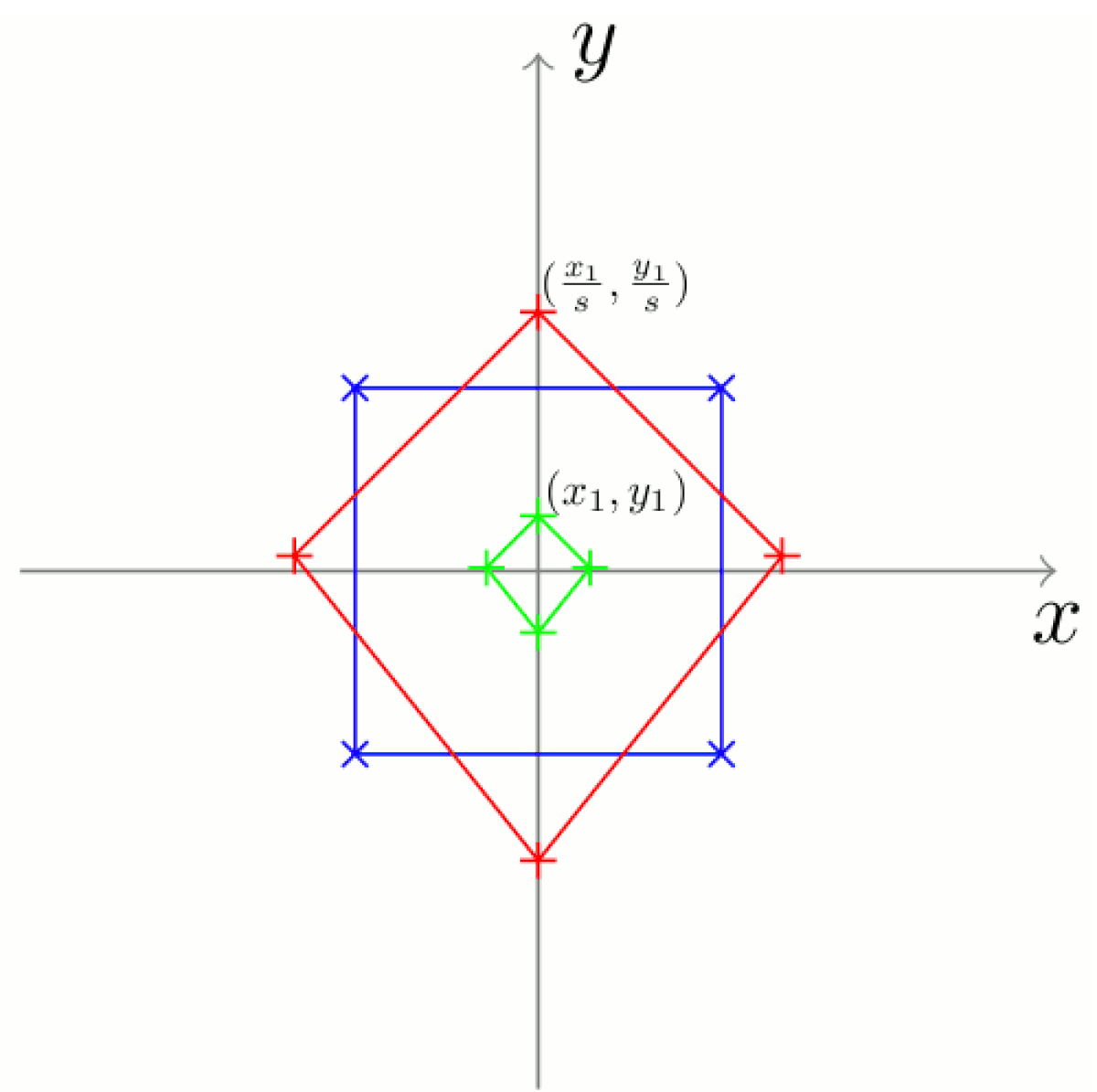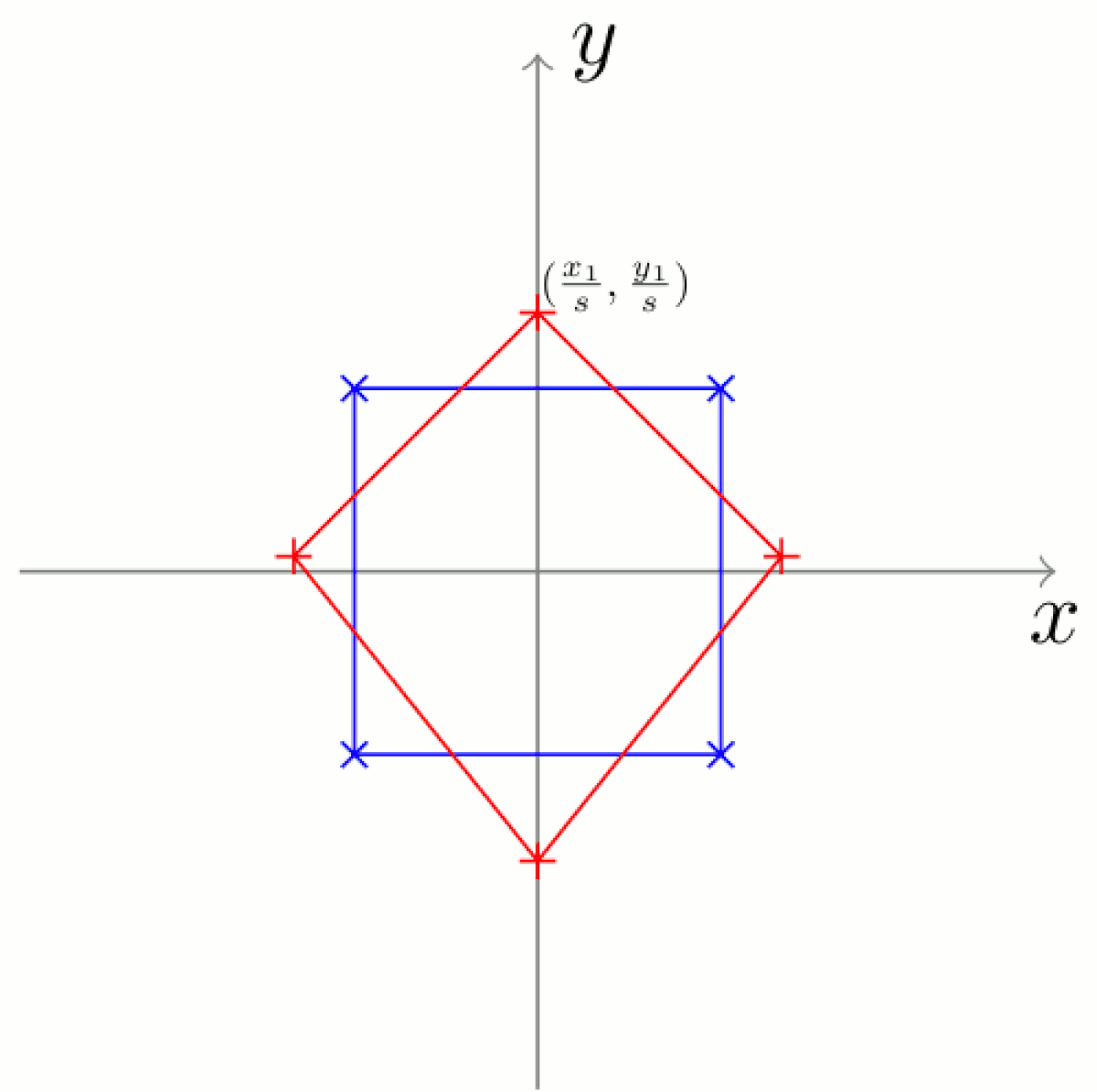
Il existe différents moyens de calculer la taille de la victime (ils dépendent principalement de la métrique choisie). Considérons ici un des plus utilisés, où la taille du quadrilatère à analyser est :

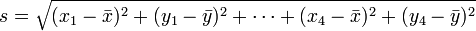
Il s'agit de donner à la forme considérée la même taille que celle de la forme de référence. Comme celle-ci est 1, il suffit d'appliquer la transformation à tous les points de la forme.

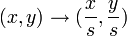
Suppression de la composante en rotation

Le quadrilatère à analyser est tourné de manière à minimiser la distance de Procuste.

La dernière étape, la plus complexe, consiste à trouver de quel angle θ il faut tourner le quadrilatère vert pour répartir au mieux entre les quatre points qui constituent les formes la différence qu'il présente avec la forme de référence.

Mathématiquement, cette différence s'exprime par une distance (qui dépend, comme la surface, de la métrique choisie) que l'on minimise en fonction de θ, en utilisant par exemple la méthode des moindres carrés.

Cette distance, une fois minimisée, s'appelle distance de Procuste et n'a d'intérêt que comparée à la distance de Procuste d'autres spécimens. Par exemple en biologie la comparaison de formes de crânes permet d'évaluer la distance entre plusieurs espèces.

Formalisme mathématique

Formalisme géométrique

Le sujet de l'analyse est une forme V, composées de k points d'intérêt de dimension n , que l'on comparera à une référence .

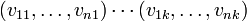
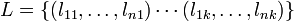
La forme fait partie d'une classe d'équivalence, générée en supprimant les composantes de translation, rotation et d'échelle.

Le problème que résout l'analyse procustéenne est la minimisation de la distance entre V et L, en utilisant uniquement sur V translations, rotations et homothéties. C'est-à-dire que l'on recherche :

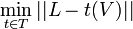
où T est l'ensemble des compositions des translations, rotations et homothéties (les mouvements que Procuste peut effectuer avec sa hache), et la norme correspondant à la distance choisie, bien souvent définie par :

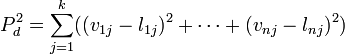
Formalisme matriciel

Le formalisme matriciel est en réalité celui qui prévaut dans la littérature (le formalisme géométrique n'ayant qu'un intérêt pédagogique).

En reprenant les notations du formalisme géométrique, le problème de Procuste revient à modifier une matrice de dimension (le voyageur) pour minimiser sa distance à un lit de Procuste , également de dimension , à l'aide d'une autre matrice , la matrice des opérations permises à Procuste, de dimension . C'est-à-dire que l'on cherchera :

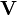
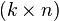
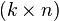
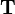
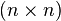
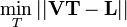
Dans le cas où est réelle, la solution du problème s'estime par :