Calcul stochastique - Définition

Équations différentielles stochastiques

Une équation différentielle stochastique (EDS) est la donnée d’une équation du type dX = μ(X,t)dt + σ(X,t)dW_t, où X est un processus aléatoire inconnu, que l’on appelle communément équation de diffusion. Intégrer l’EDS, c’est trouver l’ensemble des processus vérifiant la diffusion entière.

Intégrale de Wiener et intégrale stochastique

Intégrale de Wiener :
Notons le Mouvement Brownien (MB) par et l'intégrale de Wiener par .

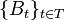
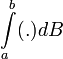
On dit qu'une fonction est une fonction en escalier (donc dense dans L²([a,b])) dans s'il existe σ une subdivision de [a,b] et s'il existe tels que :

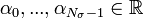
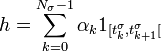
Alors, on pose :

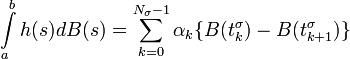
Il est clair que est une variable aléatoire gaussienne centrée de variance .

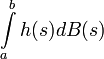
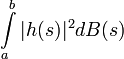
De plus, soit et H_n une suite de fonctions en escalier de . Alors, la suite converge vers une limite dans L²(Ω). De plus, cette limite ne dépend pas de la suite et est notée par .

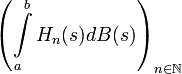
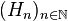
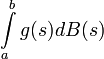
Intégrale stochastique :
Soit Z le mouvement brownien standard défini sur l’espace probabilisé (Ω,A,F,P) et σ un processus adapté à F. On suppose par ailleurs que σ vérifie :

.

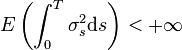
Alors, l’intégrale stochastique de σ par rapport à Z est la variable aléatoire :

.

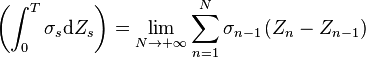
Lemme d’Itô

Soit x un processus stochastique tel qu'on ait dx = adt + bdz où z est un processus de Wiener standard.

Alors d'après le lemme d'Itô, on a pour une fonction G = G(x,t)

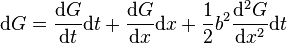
Processus d’Ornstein-Uhlenbeck

Le processus d'Ornstein-Uhlenbeck est un processus stochastique décrivant (entre autres) la vitesse d'une particule dans un fluide, en dimension 1.

On le définit comme étant la solution X_t de l'équation différentielle stochastique suivante :

,

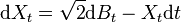
où B_t est un mouvement brownien standard, et avec X₀ une variable aléatoire donnée. Le terme dB_t traduit les nombreux chocs aléatoires subis par la particule, alors que le terme − X_tdt représente la force de frottement subie par la particule.

La formule d'Itô appliquée au processus e^tX_t nous donne :

,

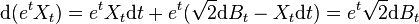
soit, sous forme intégrale :

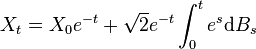
Par exemple, si X₀ vaut presque sûrement x, la loi de X_t est une loi gaussienne de moyenne xe ^{− t} et de variance 1 − e ^{− 2t}, ce qui converge en loi quand t tend vers l'infini vers la loi gaussienne centrée réduite.

Méthodes de simulation

Méthode de Monte-Carlo

Les méthodes de Monte-Carlo reposent sur la Loi des grands nombres : en répétant un grand nombre de fois une expérience, de façon (théoriquement) indépendante, on obtient une approximation de plus en plus fiable de la vraie valeur de l'espérance du phénomène observé.

De telles méthodes sont notamment utilisées en finance pour la valorisation d’options pour lesquelles il n’existe pas de formule fermée, mais uniquement des approximations numériques.

Simulation par arbres recombinants