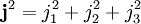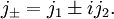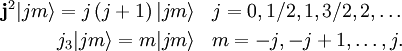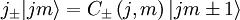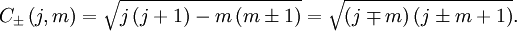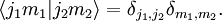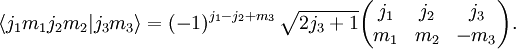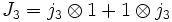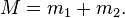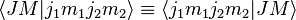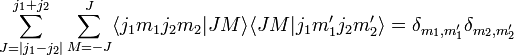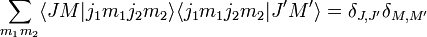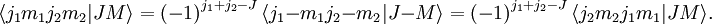Coefficients de Clebsch-Gordan - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En physique, les coefficients de Clebsch-Gordan sont des nombres qui apparaissent lors de l'étude des couplages de moment angulaire soumis aux lois de la mécanique quantique. Ils portent le nom des mathématiciens allemands Alfred Clebsch (1833-1872) et Paul Gordan (1837-1912), qui rencontrèrent un problème similaire en théorie des invariants.
En théorie des représentations, notamment des groupes de Lie compacts, ces coefficients sont utilisés pour effectuer la décomposition en somme directe du produit tensoriel de deux représentations irréductibles.
On peut définir les coefficients de Clebsch-Gordan associés au groupe SO(3) d'une manière plus directe, comme produit d'harmoniques sphériques. L'addition de spins en mécanique quantique se comprend par cette approche. Dans cet article, on utilisera la notation bra-ket de Dirac.
Notations préliminaires
Opérateurs de moment angulaire
Les opérateurs de moment angulaire sont les opérateurs hermitiens j1,j2 et j3 qui vérifient les relations suivantes :
![\left[ j_k,j_l \right] = i h/(2\pi)\sum_{m=1}^3 \varepsilon_{klm}j_m \,](https://static.techno-science.net/illustrationWebp/Definitions/autres/a/a41538c41307be231ed595b6968ef8a0_ce3a5a1f7e9718ab1817ebe76f2d786e.png)
avec
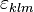
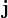
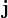
On définit également les opérateurs (j + ) et (j − ) par :
États de moment angulaire
On peut montrer que
-
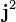
![\left[ \mathbf{j}^2, j_k \right] = 0](https://static.techno-science.net/illustration/Definitions/autres/b/bc7437357f7e8ccd86b7f705a61bfcbb_09c8d3dce15601e3ac4b764ee063031b.png)
![\left[ \mathbf{j}^2, j_k \right] = 0](https://static.techno-science.net/illustrationWebp/Definitions/autres/b/bc7437357f7e8ccd86b7f705a61bfcbb_09c8d3dce15601e3ac4b764ee063031b.png)
Lorsque deux opérateurs hermitiens commutent, ils possèdent un ensemble commun de fonctions propres. Par convention, on choisit
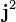
Les opérateurs (j + ) et (j − ) changent la valeur de m :
avec
Un facteur de déphasage (complexe) peut être ajouté à la définition de
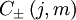
Lien avec les symboles 3—jm
Les coefficients de Clebsch-Gordan sont reliés aux symboles 3-jm, qui sont plus agréables à manipuler du fait de symétries plus simples. Cette relation s'exprime par l'équation suivante :
Définition et propriétés
Définition
Les états de moment angulaire peuvent être développés en les supposant non-couplés :
Les coefficients qui apparaissent dans le développement, notés
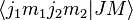
En appliquant l'opérateur :
des deux côtés de l'égalité, on montre que les coefficients de Clebsch-Gordan peuvent ne pas être nuls seulement lorsque :
Relations d'orthogonalité
On peut introduire la notation alternative, mais équivalente, suivante :
Il est alors possible d'établir deux relations d'orthogonalité :
Propriétés de symétrie
La relation de symétrie suivante est toujours valable :
