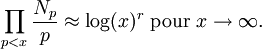Conjecture de Birch et Swinnerton-Dyer - Définition

Histoire

Au début des années 1960, Bryan Birch et Peter Swinnerton-Dyer ont utilisé l'ordinateur EDSAC au laboratoire informatique de l'Université de Cambridge pour calculer le nombre de points modulo p (désigné par N_p) pour un grand nombre de nombres premiers p sur des courbes elliptiques dont le rang était connu. À partir de ces résultats numériques, ils émirent la conjecture que N_p pour une courbe E avec un rang r obéissent à la loi asymptotique

Initialement, ceci était basé sur quelque chose de ténu montré par des points graphiques qui ont induit un certain scepticisme chez le maître de Birch, J. W. S. Cassels.

Cela les conduisit à faire une conjecture sur le comportement de la fonction L d'une courbe elliptique L(E,s) en s = 1, expressément, qu'il y aurait un zéro d'ordre r en ce point. C'était une conjecture particulièrement spectaculaire car à cette époque, le prolongement analytique de L(E,s) au point s = 1 était seulement établi pour les courbes avec multiplication complexe.

Une version plus précise de la conjecture fut ensuite proposée, décrivant le résidu du zéro en s = 1 en fonction d'invariants arithmétiques de la courbe étudiés par Cassels, Tate, Shafarevich et d'autres.

Par exemple, considérons un polynôme en deux variables f(x,y) non nul dont les coefficients sont des nombres rationnels. Supposons que la courbe projective plane associée n'ait pas de singularités. Intéressons-nous aux solutions de l'équation f(x,y) = 0 en des nombres rationnels (x,y). Alors :

• Si le degré de f est égal à 1 ou 2 (le cas d'une droite ou d'une conique), soit cet ensemble est vide (par exemple f(x,y) = x² + y² + 1), soit il est infini, auquel cas la courbe projective associée est isomorphe à une droite projective.
• Si le degré de f est supérieur ou égal à 4, Gerd Faltings a démontré que cet ensemble est fini (conjecture de Mordell).
• Si le degré de f est égal à 3, tous les cas sont possibles. Si cet ensemble est non-vide, la courbe projective associée est une courbe elliptique. La conjecture de Birch et Swinnerton-Dyer prédit alors la « taille » (le rang) de l'ensemble des solutions en fonction du prolongement méromorphe d'une série génératrice formée à partir du nombre de solutions de f(x,y)=0 modulo p pour tout nombre premier p. Elle prédit en particulier le fait de savoir si cet ensemble est fini ou infini.

Énoncé plus précis

Considérons une courbe elliptique sur . La conjecture de Birch et Swinnerton-Dyer prédit que l'ordre d'annulation de la fonction L de cette courbe elliptique en s=1 est égal au rang de cette même courbe. Elle prédit même la valeur du premier terme non-nul dans le développement limité en s=1 de cette fonction L.