Conjecture de géométrisation - Définition

Les huit géométries de Thurston

Définitions

Une géométrie modèle est une variété différentiable simplement connexe X munie d'une action transitive (différentiable) d'un groupe de Lie G sur X, dont les stabilisateurs sont compacts.

On dit qu'une géométrie modèle est maximale si G est le plus grand groupe agissant de cette manière sur X ; cette condition est parfois ajoutée à la définition d'une géométrie modèle.

Une structure géométrique sur une variété M est un difféomorphisme de M vers X/Γ pour une certaine géométrie modèle X, où Γ est un sous-groupe discret de G agissant librement sur X. Si une variété admet une structure géométrique, elle en admet une dont la géométrie modèle est maximale.

Les géométries modèles X à trois dimensions considérées par la conjecture de Thurston sont celles qui sont maximales, et pour lesquelles il existe une variété compacte admettant une structure géométrique ayant X pour modèle ; on dit qu'une variété ayant cette propriété est géométrisable. Thuston montra qu'il existe 8 géométries modèles satisfaisant ces conditions ; elles sont aussi connues sous le nom de géométries de Thurston, et détaillées ci-dessous (il existe également un nombre infini non dénombrable de géométries modèles n'admettant pas de quotients compacts).

La géométrie sphérique S³

Le stabilisateur des points de la variété est O₃(R), et le groupe G est le groupe de Lie O₄(R), de dimension 6, ayant deux composantes connexes ; la géométrie (c'est-à-dire la métrique) correspondante est l'analogue tridimensionnel de la géométrie sphérique usuelle.

Les variétés correspondantes sont précisément les variétés fermées de dimension 3 dont le groupe fondamental est fini. Parmi ces variétés, on trouve par exemple la 3-sphère, la sphère d'homologie de Poincaré (en), et les espaces lenticulaires (en)  ; une liste complète se trouve dans l'article variétés sphériques (en).

Sous l'action du flot de Ricci, les variétés ayant cette géométrie se contractent en un point en un temps fini.

La géométrie euclidienne E³

Le stabilisateur des points de la variété est O₃(R), et le groupe G est le groupe de Lie R³×O₃(R), de dimension 6, ayant 2 composantes connexes. la géométrie correspondante est la géométrie euclidienne usuelle.

Parmi les exemples, on trouve le 3-tore (S₁)³, et plus généralement le tore d'application d'un automorphisme d'ordre fini du 2-tore. Il y a exactement 10 variétés fermées ayant cette géométrie ; 6 sont orientables et 4 non-orientables.

Sous l'action du flot de Ricci, ces variétés restent invariantes globalement.

La géométrie hyperbolique H³

Le stabilisateur des points de la variété est O₃(R), et le groupe G est le groupe de Lie O_1,3(R)⁺, de dimension 6, ayant 2 composantes connexes. La géométrie correspondante est l'analogue tridimensionnel de la géométrie hyperbolique usuelle.

Il y a énormément d'exemples de cette géométrie, et leur classification n'est pas complètement comprise. L'exemple de plus petit volume connu est la variété de Weeks (en). La conjecture de géométrisation implique qu'une variété fermée est hyperbolique si et seulement si elle est irréductible, atoroïdale (en), et que son groupe fondamental est infini.

Sous l'action du flot de Ricci, ces variétés se dilatent.

La géométrie de S²×R

Le stabilisateur des points de la variété est O₂(R)×Z/2Z, et le groupe G est O₃(R)×R.Z/2Z, ayant 4 composantes connexes.

Les quatre variétés de volume fini ayant cette géométrie sont : S²×S¹, le tore de l'application antipodale de S², la somme connexe de deux copies de l'espace projectif (réel) de dimension 3, et le produit de S¹avec le plan projectif. Les deux premières sont les seuls exemples de 3-variétés qui soient indécomposables, mais non irréductibles (voir le théorème de décomposition de Milnor)  ; la troisième est le seul exemple d'une somme connexe non triviale qui puisse être munie d'une structure géométrique. Cette géométrie modèle est la seule qui ne puisse être réalisée comme métrique invariante à gauche d'un groupe de Lie de dimension 3.

Sous l'action du flot de Ricci, ces variétés convergent vers des variétés de dimension 1, c'est-à-dire des courbes.

La géométrie de H²×R

Le stabilisateur des points de la variété est O₂(R) × Z/2Z, et le groupe G est O_1,2(R)⁺ × R.Z/2Z, ayant 4 composantes connexes.

Parmi les exemples figurent le produit d'une surface hyperbolique et d'un cercle, ou plus généralement le tore d'application d'une isométrie d'une surface hyperbolique. Les variétés orientables de volume fini ayant cette géométrie ont la structure d'un fibré de Seifert (en) (les variétés non orientables, bien que fibrées en cercles, ne sont pas nécessairement des fibrés de Seifert ; leurs voisinages peuvent être des bouteilles de Klein plutôt que des tores pleins). La classification de ces variétés orientables est donnée dans l'article sur les fibrés de Seifert (en).

Sous l'action du flot de Ricci normalisé, ces variétés convergent vers des variétés de dimension 2.

La géométrie du revêtement universel de SL₂(R)

On note le revêtement universel de SL₂(R) ; c'est un fibré ayant pour base le plan hyperbolique H₂. Le stabilisateur des points de la variété est O₂(R). Le groupe G possède 2 composantes connexes ; la composante de l'identité a pour structure .

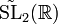
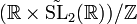
Parmi les exemples, on trouve la variété des vecteurs unité du fibré tangent d'une surface hyperbolique, et plus généralement les sphères d'homologie de Brieskorn (en) (à l'exception de la 3-sphère et de l'espace dodécahédral de Poincaré).

Sous l'action du flot de Ricci normalisé, ces variétés convergent vers des variétés de dimension 2.

La géométrie Nil

C'est un fibré ayant pour base E², dont la géométrie est celle du groupe de Heisenberg. Le stabilisateur des points de la variété est O₂(R). Le groupe G possède 2 composantes connexes, et est le produit semi-direct du groupe de Heisenberg (de dimension 3) par le groupe O₂(R) des isométries du cercle.

Parmi les variétés compactes ayant cette géométrie, on trouve le tore d'application d'une torsion de Dehn (en) d'un 2-tore, ainsi que le quotient du groupe de Heisenberg par le réseau de Heisenberg. Les variétés de volume fini ayant cette géométrie sont compactes et orientables, et ont la structure d'un fibré de Seifert (en).

Sous l'action du flot de Ricci normalisé, ces variétés convergent vers R², muni de la métrique euclidienne.

La géométrie Sol

C'est un fibré en plans ayant pour base la droite R. Le stabilisateur des points de la variété est le groupe dihédral d'ordre 8. Le groupe G possède 8 composantes connexes, et est formé des isométries de l'espace de Minkowski, et des "anti-isométries" de cet espace multipliant la métrique par -1. La composante connexe de l'identité possède un sous-groupe normal R² de groupe quotient R, où R agit sur R² en ayant deux sous-espaces propres réels, correspondant à deux valeurs propres réelles distinctes de produit 1.

Toutes les variétés de volume fini ayant cette géométrie sont compactes. Ce sont soit les tores d'une application d'Anosov du 2-tore (d'un automorphisme du 2-tore donné par une matrice 2×2 inversible dont les valeurs propres sont réelles et distinctes, telle que ), soit des quotients de ces tores par des groupes d'ordre 8 au plus.

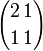
Sous l'action du flot de Ricci normalisé, ces variétés convergent (assez lentement) vers la droite R¹.