Construction d'un cercle point par point - Définition

Premier exemple

Méthode des chemins de fer

En introduction à la construction homographique d'un cercle, la méthode des chemins de fer peut être citée. On veut, à partir d'un point O d'une ligne droite, prendre un virage à droite sur un angle=45 degrés avec un rayon R=300m, malheureusement on n'a pas accès au centre du cercle. Il faut pourtant tracer l'arc de cercle point par point en plantant des piquets avec une précision suffisante.

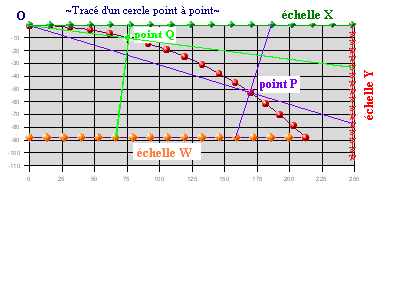
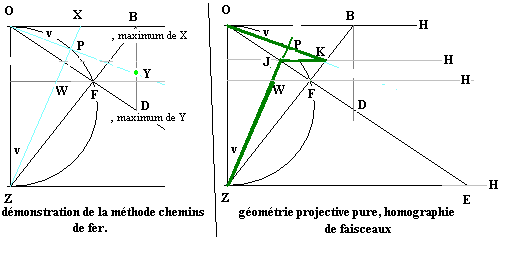
La méthode consiste à créer trois « échelles » X, Y, W graduées en n subdivisions égales, 16 par exemple, à relier les points correspondants des échelles X et W, à relier l'origine au point correspondant de l'échelle Y, le point d'intersection de ces 2 droites est un point P du cercle. Si les 16 points ne suffisent pas on peut encore subdiviser les 3 échelles en 32 parties, ou 64. Les échelles sont positionnées selon des calculs trigonométriques élémentaires. Le maximum (B) de l'échelle X est 2R*tan(angle/2), 248,53m dans notre exemple, le maximum de l'échelle Y est 2R*tan²(angle/2), le maximum de l'échelle W est R*sin(angle) et le positionnement de cette échelle est à l'ordonnée R*(1-cos(angle)).

Explication de cette méthode

La propriété du cercle utilisée ici est l'angle droit défini par un diamètre OZ. L'échelle W est positionnée judicieusement pour être homothétique de centre Z à l'échelle X, le rapport d'homothétie étant cos²(angle/2). La droite (WX) passe donc par Z, point qui à l’origine du problème est encore plus inaccessible que le centre du cercle. L'échelle Y est positionnée de façon à ce que les triangles BOZ et DBO soient semblables. Ce qui implique que lorsque l'on fait correspondre une position X à une position Y, les triangles XOZ et YBO sont semblables, les angles OBY et OZX=v sont égaux, donc les droites OY et ZX sont perpendiculaires.

Leur intersection P est sur le cercle de diamètre OZ.

Fonction homographique mise en jeu

Raisonnons à partir de l'angle v= OZX=OBY. La position de X sur son échelle est 2R*tan(v). La position de Y sur son échelle est 2R*tan(angletotal/2)*tan(v), la relation entre X et Y est

Y= tan(angletotal/2) *X

qui n'est qu'un cas particulier et dégénéré de la fonction homographique

dans laquelle c=0, d=1, b=0, a=tan(angletotal/2).

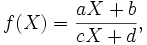
. Ceci illustre de manière analytique la propriété générale selon laquelle une conique est engendrée par l'intersection de deux faisceaux de droites en correspondance homographique, ici les faisceaux de centre Z et O.

Explication par la géométrie projective pure

Dans le plan de cette figure considéré comme plongé dans un plan projectif fondamental, on peut établir une (parmi d'autres possibles) transformation homographique entre les deux êtres mathématiques unidimensionnels que sont les faisceaux de centre Z et O. Ceci en se dispensant de travailler sur les échelles de points X et Y. On utilisera H, le point à l'infini dans la direction de l'axe OX et le faisceau de droites de centre H, c’est-à-dire le faisceau des droites parallèles à OX.

Soit la transformation T définie comme la succession de 2 tranformations projectives unidimensionnelles; la première est la transformation du faisceau Z en faisceau H en s'appuyant sur la droite (OE); la deuxième est la transformation du faisceau H en faisceau O en s'appuyant sur la droite (ZB); sur la base de 3 points connus du cercle (O, F et Z), examinons les transformations de trois droites du faisceau de départ.

la droite ZO devient HO qui est égale à HB qui devient ensuite OB, l'intersection de ZO et OB étant O, point du cercle.

la droite ZB qui est égale à ZF devient HF qui devient ensuite OF, l'intersection de ZB et OF étant F, point du cercle.

la droite ZE devient HE qui est égale à HZ qui devient ensuite OZ, l'intersection de ZE et OZ étant Z, point du cercle.

Le théorème fondamental de la géométrie projective nous assure que T est définie de manière unique par ces trois points Z, H, O et ces deux droites d'appui (OE) et (ZB). Si nous observons maintenant un droite variable du faisceau, ZX

la droite ZX qui est égale à ZJ devient HJ qui est égale à HK qui devient ensuite OK, l'intersection de ZX et OK étant P, point variable de la conique.

Or dans le triangle OKZ nous avons 2 hauteurs OF et KH qui se coupent en J qui est donc l'orthocentre. ce qui implique que l'angle en P est droit, donc que P est sur le cercle. On vérifie ainsi que la conique définie par la transformation projective unidimensionnelle T est bien le cercle considéré.

Articulation entre la géométrie projective et la géométrie euclidienne

Cet exemple en géométrie projective se résume à tracer des points P d'une conique passant par les 3 points O,Z,F et possédant 2 tangentes OB et ZE. Elle se construit par les faisceaux de centre Z et O liés par l'homographie T. Au stade de la géométrie projective, tout ce qu'on peut affirmer c'est que l'ensemble des points P est une conique.

Pour parler d'un cercle, nous avons besoin de notion métrique. Ici la notion pertinente est l'orthogonalité: les tangentes OB et ZE sont perpendiculaires à la corde ZO, l'angle F est droit, les droites du faisceau H sont toutes perpendiculaires à OZ.