Statistiques élémentaires continues - Définition
Cet article fait partie de la série Mathématiques élémentaires |
| Algèbre |
| Analyse |
| Arithmétique |
| Géométrie |
| Logique |
| Probabilité |
| Statistique |
Dans une enquête statistique, lorsque le caractère statistique peut prendre des valeurs multiples (taille, superficie, salaire…) le caractère statistique est considéré comme continu.
Traitement des données
Lorsque les résultats de l'enquête statistique sont trop nombreux pour que la liste triée des valeurs soit lisible, on préfère perdre de l'information et ranger les données par intervalles appelés classes. Il faut alors que, dans chaque classe, la répartition des valeurs soit régulière. Sinon, il faut affiner et prendre des classes plus petites. Il n'est pas indispensable que les classes soient de même amplitude, mais il est préférable de ne pas définir de classes de la forme " plus de ... " qui empêcherait alors tout traitement ultérieur (histogramme, moyenne...). On compte alors le nombre de fois où la valeur du caractère tombe dans l'intervalle [xi;xi + 1[, ce nombre est appelé effectif de la classe [xi;xi + 1[.
Exemple de tableau statistique à classes : Répartition des revenus annuels en milliers d'euros dans une population de 4370 personnes.
| Salaires | entre 0 (inclus) et 8 (exclus) |
entre 8 (inclus) et 12 (exclus) |
entre 12 (inclus) et 16 (exclus) |
entre 16 (inclus) et 20 (exclus) |
entre 20 (inclus) et 30 (exclus) |
entre 30 (inclus) et 40 (exclus) |
entre 40 (inclus) et 60 (exclus) |
Total |
| Effectifs | 306 | 231 | 385 | 1180 | 1468 | 568 | 232 | 4370 |
Les effectifs ici sont trop grands pour que l'on puisse se faire une idée simple de la répartition, on préfère alors travailler en pourcentages ou fréquences et se ramener ainsi à une population de 100.
| Salaires | entre 0 (inclus) et 8 (exclus) |
entre 8 (inclus) et 12 (exclus) |
entre 12 (inclus) et 16 (exclus) |
entre 16 (inclus) et 20 (exclus) |
entre 20 (inclus) et 30 (exclus) |
entre 30 (inclus) et 40 (exclus) |
entre 40 (inclus) et 60 (exclus) |
Total |
| Fréquences | 7,0 | 5,3 | 8,8 | 27,0 | 33,6 | 13,0 | 5,3 | 100 |
Moyenne
Puisque l’on a estimé que la répartition dans chaque classe était régulière, on peut affirmer que le milieu de la classe est représentatif de la classe. On va donc remplacer les ni individus de la classe [xi;xi + 1[ par ni individus dont le caractère statistique prendrait la valeur
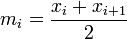
| Salaires | entre 0 (inclus) et 8 (exclus) |
entre 8 (inclus) et 12 (exclus) |
entre 12 (inclus) et 16 (exclus) |
entre 16 (inclus) et 20 (exclus) |
entre 20 (inclus) et 30 (exclus) |
entre 30 (inclus) et 40 (exclus) |
entre 40 (inclus) et 60 (exclus) |
Total |
| Effectifs | 306 | 231 | 385 | 1180 | 1468 | 568 | 232 | 4370 |
| Salaire moyen de chaque classe |
4 | 10 | 14 | 18 | 25 | 35 | 50 | total des salaires |
| Total des salaires de chaque classe |
1224 | 2310 | 5390 | 21240 | 36700 | 19880 | 11600 | 98344 |
Le salaire moyen parmi cet échantillon est donc de 98344/4370 = 22,5 soit environ 22500 Euros annuels.
La formule utilisée ici est :
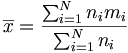
La moyenne est un des critères de position.
Représentations graphiques
Histogramme
- Voir article détaillé : Histogramme
Pour représenter graphiquement cette enquête statistique, le diagramme en bâtons est inapproprié. En effet, plus la classe est grande, plus l'effectif risque d'être important. Il faut donc représenter l'effectif de chaque classe par un rectangle dont la base est l'amplitude de la classe et dont l'aire est proportionnelle à l'effectif ou à la fréquence. Ce diagramme s'appelle un histogramme.
Exemple: si 1% est représenté par 1 carreau unité.
| Salaires | entre 0 (inclus) et 8 (exclus) |
entre 8 (inclus) et 12 (exclus) |
entre 12 (inclus) et 16 (exclus) |
entre 16 (inclus) et 20 (exclus) |
entre 20 (inclus) et 30 (exclus) |
entre 30 (inclus) et 40 (exclus) |
entre 40 (inclus) et 60 (exclus) |
| Fréquences | 7,0 | 5,3 | 8,8 | 27,0 | 33,6 | 13,0 | 5,3 |
| Amplitudes ai = xi + 1 − xi |
8 | 4 | 4 | 4 | 10 | 10 | 20 |
| Hauteurs hi = fi / ai |
0,9 | 1,3 | 2,2 | 6,8 | 3,4 | 1,3 | 0,3 |
Il ne reste plus qu'à tracer l'histogramme:
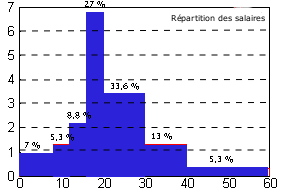
Remarque : si les amplitudes des classes sont identiques, les hauteurs des rectangles sont proportionnelles aux effectifs ou aux fréquences.
Polygone des fréquences cumulées
Puisque la répartition dans chaque classe est supposée régulière, on peut admettre que l'accroissement de la fréquence est une fonction linéaire. On trace alors le polygone des fréquences cumulées croissantes qui permet de lire la fréquence de la classe [x1;x] pour tout x.
Au préalable, il faut remplir le tableau des fréquences cumulées:
| xi | 0 | 8 | 12 | 16 | 20 | 30 | 40 | 60 |
| Fréquences cumulées croissantes | 0 | 7 | 12,3 | 21,1 | 48,1 | 81,7 | 94,7 | 100 |
Il ne reste plus qu'à tracer le polygone:
On peut construire de même le polygone des fréquences cumulées décroissantes.
Variance et écart type
Les formules précédemment établies pour les variables discrètes restent valables à condition de remplacer xi par mi milieu de la classe [xi;xi + 1[:
-
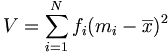
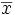
-
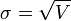
L'écart type est une des critères de dispersion

















































