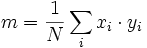Dépouillement d'une courbe - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En sciences expérimentales, le relevé de données se représente fréquemment sur un graphique et prend alors souvent la forme d'une courbe. Le dépouillement de la courbe est l'opération qui consiste à extraire des informations de cette courbe ; l'information ne provient pas des valeurs individuelles des points, mais de leur organisation, de la forme de la courbe.
Lorsque cette courbe est un spectre, on parle de dépouillement d'un spectre.
Origine de la courbe
Les valeurs peuvent être relevées individuellement (mesure manuelle, lecture sur un appareil, acquisition automatique) et placées sur un graphique (points placés à la main sur du papier millimétré, ou valeurs entrées dans un tableur ou un logiciel de représentation de données), ou bien le graphique peut être directement issu de l'acquisition (tracé sur une table traçante, acquisition automatique générant directement le graphique).
Le traitement peut être manuel, « à la règle et au crayon », ou informatisé. Lorsque la courbe est une courbe analogique (tracé par une table traçante), il est possible de numériser la courbe. Cela peut se faire à l'aide d'un scanner puis d'un logiciel de traitement d'image (pour reconnaître les axes et la courbe), ou bien à l'aide d'une table de numérisation (sorte de souris transparente, le clic permettant d'enregistrer le point).
Traitement automatisé
Lorsque les points sont relevés sous forme de valeur, il est alors intéressant de faire les traitements par informatique.
Lissage
Régression
La régression, appelée en anglais profile fitting (ajustement de profil), peut s'effectuer avec tout type de fonction.
La régression permet de résoudre de manière efficace les problèmes de superposition de pics.
Travail sur les pics
On peut, comme pour le traitement manuel, prendre un fond linéaire en définissant des positions fixes. Mais on peut aussi ajuster un polynôme sur la courbe que l'on obtient lorsque l'on enlève les pics.
On peut ajuster le pic par régression (par exemple fonction gaussienne, pseudo-fonction de Voigt…) ; dans ce cas-là, les paramètres du pic peuvent être déduits des paramètres de la fonction.
Position et hauteur du pic
La position du sommet peut être déterminée en ajustant une parabole aux points situés autour du point le plus haut.
Si le pic est symétrique, on peut aussi utiliser la moyenne pondérée m des points :
pour les N points constituant le pic.
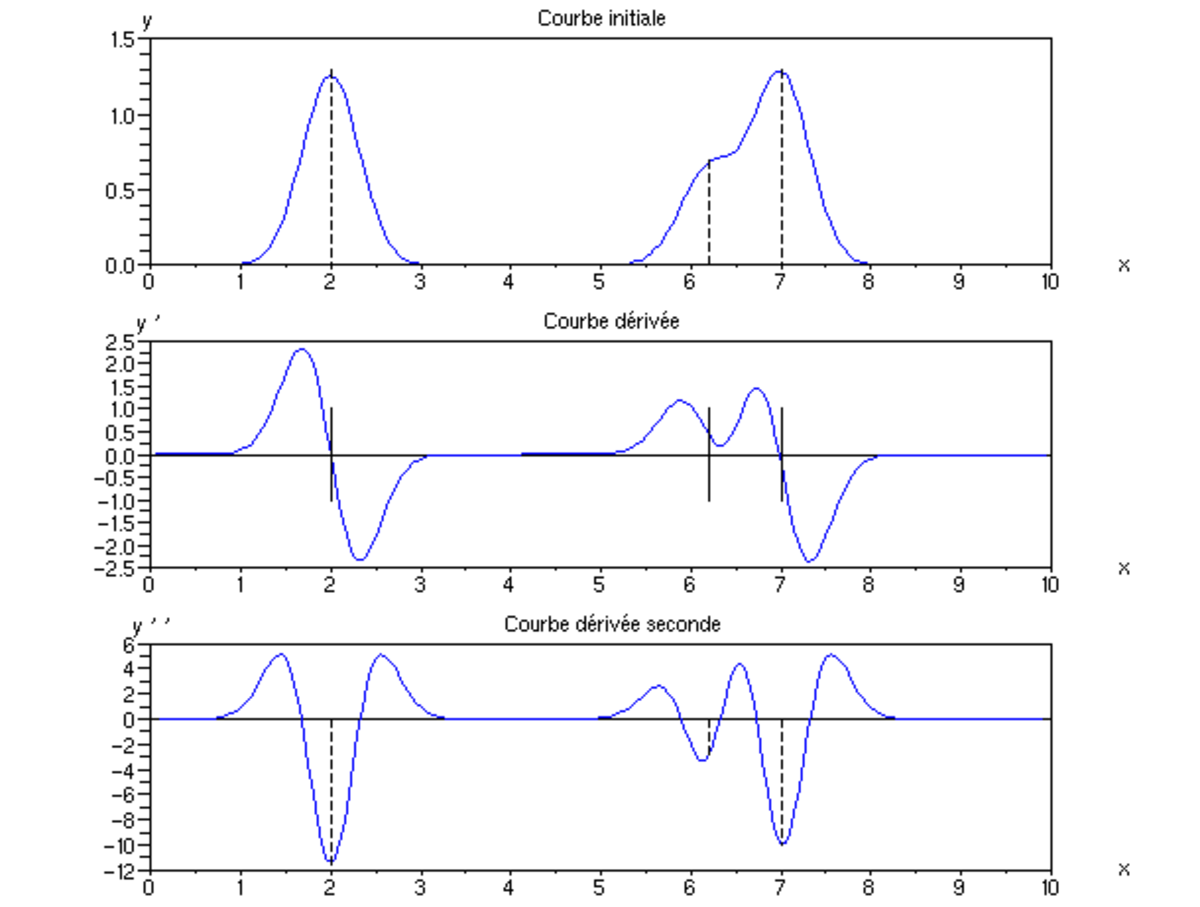
On peut également déterminer la position du sommet par la dérivée, qui présente une forme caractéristique pic positif-pic négatif et passe par zéro à l'endroit du sommet, ou bien par la dérivée seconde qui présente alors un minimum local. L'utilisation de la dérivée seconde permet de prendre en compte la superposition de deux pics, lorsqu'un des pics apparaît comme un épaulement de l'autre : à cet endroit, la dérivée ne s'annule pas puisque la tangente n'est pas horizontale ; cela revient à détecter les extrema de courbure. Les inversions de courbure, les points d'inflexion, se détectent également très bien : ce sont les intersections de la dérivée seconde avec l'axe y'' = 0.
La dérivation à intérêt à se faire sur la courbe lissée : en effet, le bruit aléatoire consistant en des variations d'un point sur l'autre, il introduit une forte perturbation de la dérivation (le δx étant petit, le taux de variation est très grand). Si l'on utilise l'algorithme de Savitzky-Golay, on peut utiliser la dérivée du polynôme au milieu du segment glissant.
Surface et largeur du pic
La surface, nette ou brute, peut être déterminée par intégration numérique.
On peut alors définir une autre largeur : la largeur intégrale, qui est le rapport de la surface nette sur la hauteur nette. C'est la largeur d'un rectangle qui aurait la même surface nette et la même hauteur nette que le pic.
Déconvolution de pics
Un pic correspond à un phénomène physique. Lorsque des phénomènes génèrent des pics proches, ceux-ci peuvent se recouvrir ; on parle parfois d'interférence. Voir aussi l'article Résolution (optique).
Si l'on a un modèle mathématique pour la forme des pics, on peut les séparer. On parle de désommation, ou encore de déconvolution.
Dans d'autre cas, la forme du pic dépend de plusieurs paramètres. Le pic est alors la somme ou le produit de convolution de fonctions élémentaires, la forme de chaque fonction dépendant des paramètres. L'opération permettant de décomposer les pics en fonctions élémentaires porte aussi le nom de déconvolution.