Déterminant de Gram - Définition

Introduction

En géométrie euclidienne ou hilbertienne, le déterminant de Gram permet de calculer des volumes et de tester l'indépendance linéaire d'une famille de vecteurs. Il associe des calculs de produits scalaires et d'un déterminant. Son nom est un hommage au mathématicien danois Jørgen Pedersen Gram (1850-1916).

L'article déterminant montre comment définir le volume orienté d'un parallélotope formé par n vecteurs en dimension n, sans nécessité de munir l'espace d'un produit scalaire. Les déterminants de Gram demandent de définir un tel produit scalaire, permettent le calcul des volumes des parallélotopes de toutes dimensions, mais sans notion d'orientation.

Plus généralement, il est possible de calculer des déterminants de Gram sur un espace quadratique. En dimension finie, le discriminant d'une forme bilinéaire symétrique est un cas particulier de déterminant de Gram.

Définition

Soit E un espace préhilbertien réel. Si x₁,..., x_n sont n vecteurs de E, la matrice de Gram associée est la matrice symétrique de terme général (x_i|x_j). Le déterminant de Gram est le déterminant de cette matrice

Déterminant de Gram

Propriétés

Écriture à l'aide d'une matrice représentative

Soit B une base orthonormale de l'espace engendré par les x_i ; elle contient vecteurs. Soit X la matrice représentative du système de vecteurs x_i dans B. C'est une matrice de taille , dont chaque colonne contient les composantes d'un des vecteurs x_i. La matrice de Gram n'est autre que ^tX X.

Effet d'opérations élémentaires

• la multiplication d'un des vecteurs par le réel a provoque une multiplication du déterminant de Gram par a²
• le déterminant de Gram est invariant par permutation des x_i
• l'ajout à un vecteur d'une combinaison linéaire des autres vecteurs laisse invariant le déterminant de Gram

Propriétés

• si pour tout , alors on a
• le déterminant de Gram d'une famille de n vecteurs est toujours positif
• il est nul si et seulement si la famille est liée (ce qui est un cas particulier de l'énoncé sur le rang de la famille de Gram)

Démonstration

Si la famille est liée, est combinaison linéaire des autres x_i ; donc

Si la famille est libre, alors d=n, X est une matrice carrée inversible comme matrice de passage d'une base à une autre. Le déterminant de Gram est (detX)² qui est strictement positif.

Application à la distance d'un vecteur à un sous-espace vectoriel

Soit F un sous-espace vectoriel de dimension finie n de E . Soient x₁,..., x_n, n vecteurs formant une base de F. Tout vecteur x de E admet un projeté orthogonal p(x) sur F.

On a : x = x - p(x) + p(x). Or p(x) est combinaison linéaire des x_i donc :

Puis :

Mais x - p(x) est par définition orthogonal aux x_i, donc :

Ainsi :

Application au calcul des composantes d'un vecteur dans une base quelconque

Soit F un sous-espace vectoriel de dimension finie n de E, muni d'une base . Soit .

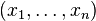
On pose . Alors pour tout on a la relation

Il ne reste plus qu'à trouver le signe de chaque p_j

Matrice de Gram

Les vecteurs colonnes de la matrice de Gram admettent les mêmes relations de dépendance linéaire (dans l'espace Rⁿ des n-uplets de réels) que les vecteurs x_i dans E ; c'est-à-dire, si on note C₁,..., C_n la famille des vecteurs colonnes de la matrice de Gram, pour toute famille de réels a₁,..., a_n :

si et seulement si

Il s'ensuit que la matrice de Gram de la famille de vecteurs x₁,..., x_n a le même rang que ladite famille de vecteurs.